Il punto di partenza – dando per scontato tutto ciò che c’è “a monte”, salvo riprendere il discorso in fasi successive …da qualche parte dovevo pur iniziare! 🙂 – è relativo a un sistema ad anello aperto lineare, tempo continuo, stazionario e a dimensione finita descritto dalla rappresentazione con lo spazio di stato in forma implicita per un sistema proprio:

\left \{  \begin{array}{ll} \dot{x}(t)=Ax(t)+Bu(t)\\y(t)=Cx(t)+Du(t) \end{array} \right.

oppure, per un sistema strettamente proprio:

\left \{  \begin{array}{ll} \dot{x}(t)=Ax(t)+Bu(t)\\y(t)=Cx(t) \end{array} \right.

Il sistema ad anello chiuso viene descritto dalla seguente rappresentazione con lo spazio di stato:

\left \{  \begin{array}{ll} \dot{x}(t)=(A-BC)x(t)+Bu(t)\\y(t)=Cx(t) \end{array} \right.

La Laplace Trasformata della seconda forma (sistema strettamente proprio) da luogo ad una funzione di trasferimento ingresso-uscita del sistema che nella sua forma generica è possibile scrivere come:

F(s)=\frac{B_{n-1}s^{n-1}+B{n-2}s^{n-2}+\dots+B_{1}s+B_0}{d(s)}=\frac{N(s)}{d(s)}

laddove, per la notazione riportata, N(s) è una matrice di dimensione [pxq]:

\underbrace{\left[\begin{matrix} n_{11}(s) & n_{12}(s) & \dots & n_{1q}(s) \\ n_{21}(s) & n_{22}(s) & \dots & n_{2q}(s) \\ \vdots       & \vdots       & \ddots & \vdots \\ n_{p1}(s) & n_{p2}(s) & \dots & n_{pq}(s) \end{matrix}\right]}_{\mathbf{N(s)}}

Per procedere con l’analisi un minimo di dimostrazioni vanno affrontate al fine di arrivare a capire perché un dato termine da luogo ad uno specifico diagramma per poi arrivare ad ottenere da una funzione di trasferimento gli associati diagrammi di Bode.

Rappresentazioni di una Funzione di Trasferimento

Una f.d.t. F(s) per un sistema a tempo continuo, stazionario, lineare e a dimensione finita, coincide con la Laplace Trasformata della risposta impulsiva ed è costituita da funzioni razionali proprie/strettamente proprie nella variabile s. Le rappresentazioni generalmente (ma non esclusivamente) più utilizzate vedono il rapporto di polinomi e la rappresentazione mediante poli e zeri.

Ipotizzando sistemi a un solo ingresso e ad una sola uscita, così evitiamo di portarci dietro delle matrici, la rappresentazione tramite rapporto di polinomi per f.d.t strettamente proprie (grado del numeratore minore del grado del denominatore) può essere scritta come:

F(s)=\frac{b_{n-1}s^{n-1}+b_{n-2}s^{n-2}+...+b_{1}s+b_0}{s^n+a_{n-1}s^{n-1}+...+a_1 s+a_0}\kern{1cm}(1)

La rappresentazione mediante poli e zeri fa riferimento alla forma fattorizzata di Evans, ovvero alle espressioni fattorizzate poli-zeri funzioni delle soluzioni dei polinomi a numeratore e denominatore. In termini generali è possibile scrivere:

F(s)=\frac{N(s)}{D(s)}=K \frac{\prod_{i=1}^m (s-z_i)^{\nu_i}}{\prod_{i=1}^n(s-p_i)^{\mu_i}}=K \frac{(s-z_1)(s-z_2)...(s-z_{m-1})(s-z_m)}{(s-p_1)(s-p_2)...(s-p_{n-1})(s-p_n)}

dove ν_i≥1  è la molteplicità del generico zero z_i, e μ_i≥1 è la molteplicità del generico polo p_i. Nella formula, nell’ultima uguaglianza, si è ipotizzato poli e zeri a molteplicità unitaria. Infine K è il rapporto tra i coefficienti di ordine massimo del numeratore e del denominatore.

È possibile ulteriormente generalizzare la formula inserendo i termini trinomi a rappresentare coppie di poli/zeri complessi coniugati separati da quelli reali nonché un eventuale polo di molteplicità μ₀ nell’origine così come un eventuale zero di molteplicità ν₀ nello stesso punto:

F(s)=\frac{N(s)}{D(s)}=K \frac{\prod_{i=1}^{m_1} (s-z_i)^{\nu_i} \prod_{j=1}^{m_2} [(s-\beta_j)^2 + \gamma_j^2]^{\nu_j}}{s^{\mu_0 - \nu_0} \prod_{i=1}^{n_1} (s-p_i)^{\mu_i} \prod_{j=1}^{n_2} [(s-\alpha_j)^2 + \delta_j^2]^{\mu_j}}\kern{1cm}(2)

per la quale, poiché si ipotizza una funzione strettamente propria, m=m₁+2m₂<n₁+2n₂=n con m₁, 2m₂, n₁ e 2n₂ ad indicare rispettivamente il numero di zeri a parte reale, zeri complessi e coniugati, poli e poli complessi e coniugati. È evidente con nel suddetto conteggio rientrino eventuali presenze di poli/zeri nell’origine comprensivi delle rispettive molteplicità.

Dalla precedente formula è possibile ottenere la forma con costanti di tempo, detta forma canonica di Bode (la forma preferita poiché permette di avere subito il guadagno k e il termine ω_n allorquando sia uguale a 1 il termine di ordine 0 del polinomio di secondo grado) e nella quale sono esplicitate le costanti di tempo \tau_i^p - \tau_i^z per poli e zeri a parte reale, così come smorzamenti \xi_j^p - \xi_j^z e pulsazioni naturali \omega_{n_j}^p - \omega_{n_j}^z per i poli complessi coniugati.

Sviluppando il termine dentro parentesi quadre, ad esempio al numeratore (medesima procedura per termini analoghi al denominatore) risulta, per parte reale e coefficiente dell’immaginario di una coppia di zeri complessi coniugati:

z_{1,2}=\beta\pm\jmath\gamma

essendo in generale:

• Pulsazione naturale per la coppia di zeri complessi e coniugati \omega_n^z=\sqrt{\beta^2+\gamma^2};
• Coefficiente di smorzamento per la coppia di zeri complessi coniugati:
  \xi^z=-\frac{\beta}{\omega_n^z}=-\frac{\beta}{\sqrt{\beta^2+\gamma^2}}

Lo sviluppo del termine j-esimo tra parentesi quadre, sostituendone i valori, da luogo a:

s^2+\beta_j^2-2\beta_j s+\gamma_j^2 = s^2-2\beta_js+(\omega_{n_j}^z)^2=s^2+2\xi_j^z\omega_{n_j}^zs+(\omega_{n_j}^z)^2

nella quale mettendo in evidenza il termine noto (termine di grado zero), risulta:

s^2+2\xi_j\omega_{n_j}^zs+(\omega_{n_j}^z)^2=(\omega_{n_j}^z)^2(1+2\xi_j^z\frac{s}{\omega_{n_j}^z}+\frac{s^2}{(\omega_{n_j}^z)^2})

Per gli zeri a parte reale si può invece scrivere:

(s-z_i)=-z_i(-s\frac{1}{z_i}+1)=-z_1(1-s\frac{1}{z_i})=-z_1(1+\tau_i^zs)

avendo posto:

\tau_i^z=-\frac{1}{z_i}

In definitiva la rappresentazione completa a costanti di tempo, dopo sostituzione, risulta:

F(s)=k\frac{\prod_{i=1}^{m_1}(1+\tau_i^zs)^{\nu_i} \prod_{j=1}^{m_2}[1+2\xi_j^z\frac{s}{\omega_{n_j}^z}+\frac{s^2}{(\omega_{n_j}^z)^2}]^{\nu_j}}{s^{\mu_0-\nu_0} \prod_{i=1}^{n_1}(1+\tau_i^ps)^{\mu_i} \prod_{j=1}^{n_2}[1+2\xi_j^p\frac{s}{\omega_{n_j}^p}+\frac{s^2}{(\omega_{n_j}^p)^2}]^{\mu_j}}\kern{1cm}(3)

e dove il termine k è pari a:

k=K\frac{\prod_{i=1}^{n_1} (\tau_i^p)^{\mu_i} \prod_{j=1}^{m_2} (\omega_{n_j}^z)^{2\nu_j}}{\prod_{i=1}^{n_1} (\tau_i^z)^{\nu_i} \prod_{j=1}^{n_2} (\omega_{n_j}^p)^{2\mu_j}}\kern{1cm}(4)

Da questo primo risultato si evince come la F(s) risulti univocamente determinata nel momento in cui si conoscono i coefficienti, gli zeri e i poli con associate molteplicità.

Diagrammi di Bode

Il risultato ottenuto nel paragrafo precedente, imponendo la condizione s=\jmath\omega, permette di ottenere la funzione di risposta armonica riportata di seguito:

F(\jmath\omega)=k\frac{\prod_{i=1}^{m_1}(1+\tau_i^z\jmath\omega)^{\nu_i} \prod_{j=1}^{m_2}[1+2\xi_j^z\frac{\jmath\omega}{\omega_{n_j}^z}+\frac{(\jmath\omega)^2}{(\omega_{n_j}^z)^2}]^{\nu_j}}{(\jmath\omega)^{\mu_0-\nu_0} \prod_{i=1}^{n_1}(1+\tau_i^p\jmath\omega)^{\mu_i} \prod_{j=1}^{n_2}[1+2\xi_j^p\frac{\jmath\omega}{\omega_{n_j}^p}+\frac{(\jmath\omega)^2}{(\omega_{n_j}^p)^2}]^{\mu_j}}\kern{1cm}(5)

Per la sua rappresentazione si fa generalmente ricorso a diagrammi cartesiani uno per il modulo |F(\jmath\omega)| e uno per la fase \phase{F(\jmath\omega)}. Entrambi i diagrammi fanno uso di una scala logaritmica per l’asse delle ascisse (pulsazioni in rad/s) permettendo così di rappresentare in maniera dettagliata la grandezza di interesse al variare di ω in intervalli estesi.

Considerando la forma esponenziale di un numero complesso è noto come esso sia rappresentabile mediante due valori reali detti modulo e fase nella forma, con riferimento alla F(\jmath\omega):

F(\jmath\omega)=|F(\jmath\omega)| e^{\jmath\phase{F(\jmath\omega)}}

che moltiplicata al primo e secondo membro per \ln e ricordando le proprietà dei logaritmi è possibile scrivere:

\ln F(\jmath\omega)=\ln(|F(\jmath\omega)| e^{\jmath\phase{F(\jmath\omega)}})=\ln |F(\jmath\omega)| + \ln e^{\jmath\phase{F(\jmath\omega)}}=\\[1.5em]=\ln |F(\jmath\omega)|+\jmath\phase{F(\jmath\omega)}\kern{1cm}(6)

Tipicamente la rappresentazione della scala logaritmica è in base 10, ma il passaggio comporta solo l’introduzione di un fattore di scala di valore pari a:

\log_{10}(x)=\frac{\ln(x)}{\ln(10)}

infatti:

y=\log_a(x) \Longleftrightarrow a^y=x

effettuando il logaritmo naturale del primo e del secondo membro, ricordando sempre le proprietà dei logaritmi:

\ln(a^y)=\ln(x)\Rightarrow y\ln(a)=\ln(x)\Rightarrow y=\frac{\ln(x)}{\ln(a)}

ovvero, ricordando che y=\log_a(x):

\log_a(x)=\frac{\ln(x)}{\ln(a)}

c.v.d.

 

La base più utilizzata per il logaritmo è la 10 poiché permette agilmente di suddividere l’asse delle ascisse in decadi e questo sia per il diagramma dei moduli sia per il diagramma delle fasi. Diverse, invece, le rappresentazioni delle grandezze sull’asse delle ordinate. Per il diagramma dei moduli la scala è una rappresentazione lineare in dB definita come:

|F(\jmath\omega)|_{dB}\triangleq20\log_{10}|F(\jmath\omega)|

Per il diagramma delle fasi la rappresentazione è lineare, tipicamente in gradi, talvolta in radianti.

Perché queste diverse rappresentazioni? Per una semplice comodità, infatti dovendo nella stragrande maggioranza dei casi tracciare il diagramma del prodotto e/o rapporto di due o più fattori per i quali sono noti i diagrammi logaritmici allora il diagramma complessivo, per le scelte testé indicate, si traduce nella somma algebrica dei moduli e delle fasi dei singoli fattori.

Fattori che, come visibile dalla funzione di risposta armonica (5), possono essere di diverso tipo:

• Fattore costante k;
• Fattore monomio \jmath\omega ;
• Fattori binomi del tipo (1+\jmath\omega\tau);
• Fattori trinomi 1+2\xi\frac{\jmath\omega}{\omega_n}+(\frac{\jmath\omega}{\omega_n})^2;

A rigore manca il fattore esponenziale del tipo e^{\jmath\omega\tau} che verrà trattato in un secondo momenti in separata sede. Ognuno di questi fattori fornisce un proprio contributo ai diagrammi del modulo e della fase, contributi riportati dettagliatamente nel seguito.

Fattore costante k

È facile verificare come nel diagramma dei moduli il valore k comporti una traslazione del livello poiché risulta |k|_{dB}=20\log_{10}|k| . Per la fase se k>0 allora \phase{k}=0^\circ, se k<0 la fase è -180°.

Fattore monomio a numeratore (zero nell’origine)

Per la (6) è possibile scrivere:

\log_{10}\jmath\omega=\log_{10}\omega+\jmath\frac{\pi}{2}

il cui modulo in dB è pari a:

|\jmath\omega|_{dB}=20\log_{10}(\omega)

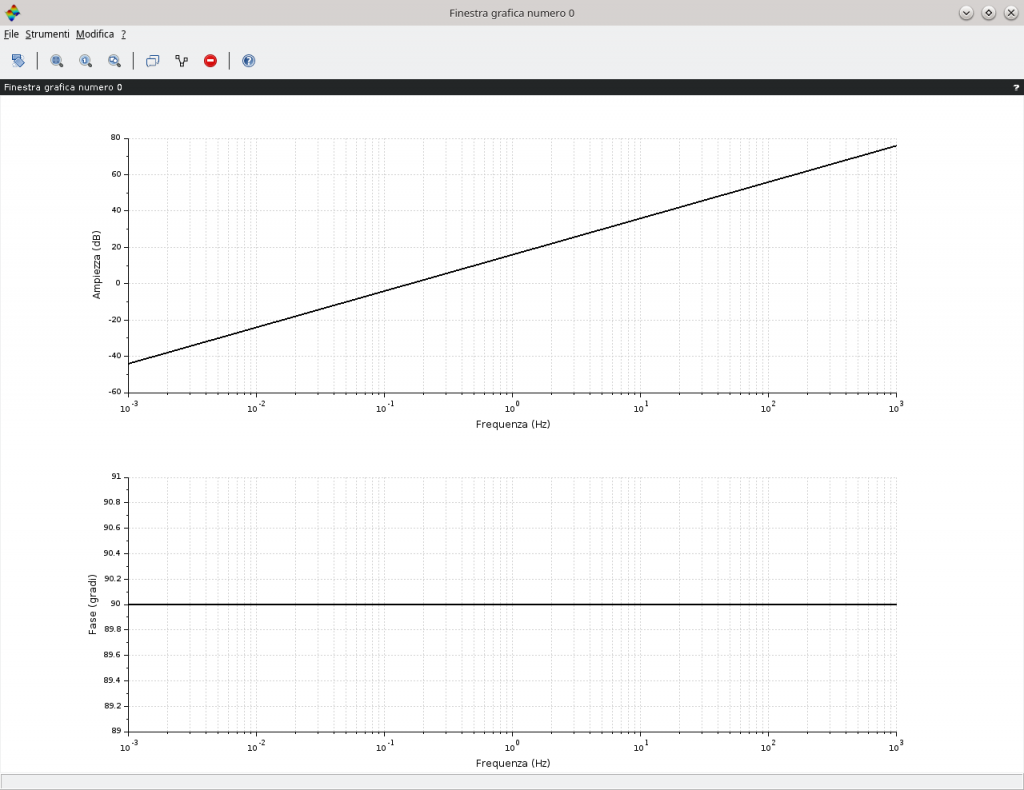
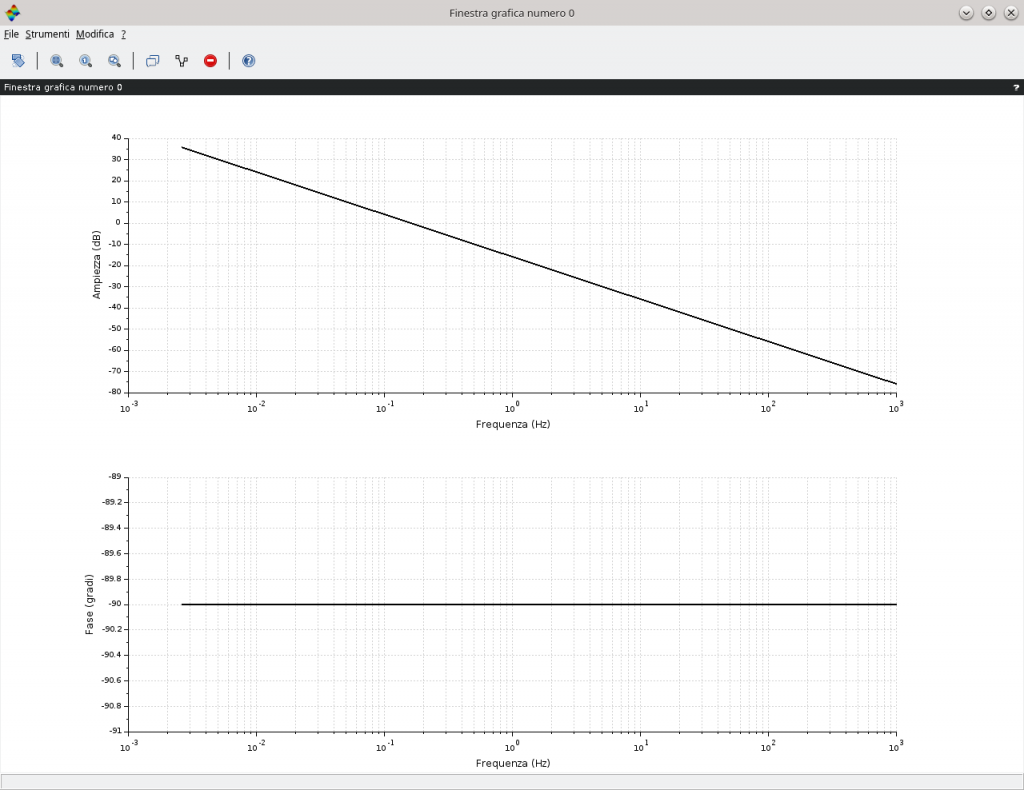
ed essendo l’asse delle pulsazioni (asse delle x) logaritmica allora un fattore monomio a numeratore contribuisce con una retta con pendenza positiva e pari 20dB/decade che attraversa il valore 1rad/s a 0dB. Per la fase si è in presenza di un immaginario puro quindi il contributo è costante per ogni valore della pulsazione e pari a \frac{\pi}{2} \enspace \forall\omega\gt0. La situazione è visibile nell’immagine in basso con l’uso di Scilab. Osservare come l’ascissa venga riportata in frequenza pertanto l’attraversamento a 0dB avviene alla frequenza di \frac{1}{2\pi}\eqsim 0,159Hz.

 

La presenza di un termine di molteplicità superiore a 1, generalizzando del tipo (\jmath\omega)^h, da luogo a un diverso andamento del diagramma del modulo e del diagramma delle fasi. Ad esempio se h=3 significa avere un termine a numeratore del tipo (\jmath\omega)^3 ovvero, ricordando la proprietà dei logaritmi,

|(\jmath\omega)^3|_{dB}=20\log_{10}(\omega)^3=3\times 20\log_{10}(\omega)

quindi una retta con pendenza pari a 60dB/decade. Se h=2 si avrebbe una retta con pendenza 40dB/decade e così via discorrendo. Per verificarlo si può fare uso di Scilab e del seguente breve listato da riportare riga dopo riga nella console del suddetto programma.

// Variabile w come pulsazione per valori tra 0,001 e 1000 con 1000 valori
w=logspace(-3,3,1000);
// Definiamo 3 rapporti di polinomi in jω - s, s^2 e s^3
F1jw=horner(poly([0 1],'s','c'),%i*w)./horner(poly([1 0],'s','c'),%i*w);
F2jw=horner(poly([0 0 1],'s','c'),%i*w)./horner(poly([1 0],'s','c'),%i*w);
F3jw=horner(poly([0 0 0 1],'s','c'),%i*w)./horner(poly([1 0],'s','c'),%i*w);
// Ora si calcola il modulo di ogni singola funzione di risposta armonica
modF1jw=20*log10(abs(F1jw));
modF2jw=20*log10(abs(F2jw));
modF3jw=20*log10(abs(F3jw));
// Ora si calcola la fase di ogni singola funzione di risposta armonica
faseF1jw=phasemag(F1jw);
faseF1jw=phasemag(F2jw);
faseF3jw=phasemag(F3jw);
// Visualizzazione risultati
plot2d(w,[modF1jw',modF2jw',modF3jw'],logflag='ln'),xgrid
plot2d(w,[faseF1jw',faseF2jw',faseF3jw'],logflag='ln'),xgrid

Il risultato è visibile in basso; in nero il termine \jmath\omega pendenza 20dB/decade. In blu il termine (\jmath\omega)^2 pendenza 40dB/decade. Infine in verde il termine (\jmath\omega)^3 da 60dB/decade. Stesso discorso si può ripetere per il diagramma delle fasi per la quale ogni aumento della molteplicità di una unità comporta uno sfasamento di \frac{\pi}{2} aggiuntivi (da ricordare che la periodicità dell’arcotangente è pari a π).

 

Fattore monomio a denominatore (polo nell’origine)

Il termine in questione è \frac{1}{\jmath\omega} per il cui modulo si può scrivere:

\left|\frac{1}{\jmath\omega}\right|_{dB}=20\log_{10}\left|\frac{1}{\jmath\omega}\right|=-20\log_{10}(\omega) \to \forall\omega\gt0

ad indicare una retta con pendenza negativa di -20dB/decade che intercetta l’asse a 0dB alla pulsazione di 1rad/s ovvero alla frequenza circa di 0,159Hz.

Per la fase, essendo ancora in presenza di un immaginario puro, il contributo è costante per ogni valore della pulsazione e pari a -\frac{\pi}{2} \enspace \forall\omega\gt0.

 

Per molteplicità superiori a 1 valgono considerazioni analoghe a quanto fatto per il termine monomio a numeratore solo che in questo caso si avranno -40dB/decade per molteplicità 2, -60dB/decade per molteplicità 3 e così via. Il diagramma delle fasi vedrà una riduzione di fase pari a -\frac{\pi}{2} per ogni molteplicità aggiuntiva.

Fattore binomio a numeratore (zeri reali)

Si è in presenza di un fattore del tipo (1+\jmath\omega\tau^z) – dove la z indica un apice e non un elevamento a potenza! – per il cui modulo è possibile scrivere:

|1+\jmath\omega\tau^z|_{dB}=20\log_{10}|1+\jmath\omega\tau^z|=2\times 10\log_{10}\sqrt{1+\omega^2(\tau^z)^2}=\\[1.5em]=10\log_{10}(1+\omega^2(\tau^z)^2)

il quale, come è evidente, varia il suo valore al variare della pulsazione da zero ad infinito. Di preciso in bassa frequenza:

|1+\jmath\omega\tau^z|_{dB}=|1|_{dB}=0 \space\space \omega\rightarrow 0^+ \space\space (\log_{10} \omega \rightarrow -\infty)

mentre in alta frequenza risulta:

|1+\jmath\omega\tau^z|_{dB}\eqsim|\jmath\omega\tau^z|_{dB}=20\log(\omega\tau^z)\rightarrow \infty \space\space \omega\rightarrow \infty \space\space (\log_{10} \omega \rightarrow \infty)

Queste due semirette rappresentano il diagramma asintotico del modulo, semirette che si incontrano in ω=ω_n nel cui punto si ha anche il massimo errore di approssimazione, errore che verrà calcolato nel seguito.

Per l’argomento \phase{(1+\jmath\omega\tau^z})=\arctan(\omega\tau^z) analizzandone il comportamento per valori della pulsazione da zero ad infinito risulta:

\arctan(\omega\tau^z) \left \{ \begin{array}{ll}0 \space\space\space \omega\rightarrow0^+ \\ \frac{\pi}{4} \space\space\space \omega=\omega^z=\frac{1}{\tau^z} \\ \frac{\pi}{2} \space\space\space \omega\rightarrow\infty\end{array} \right.

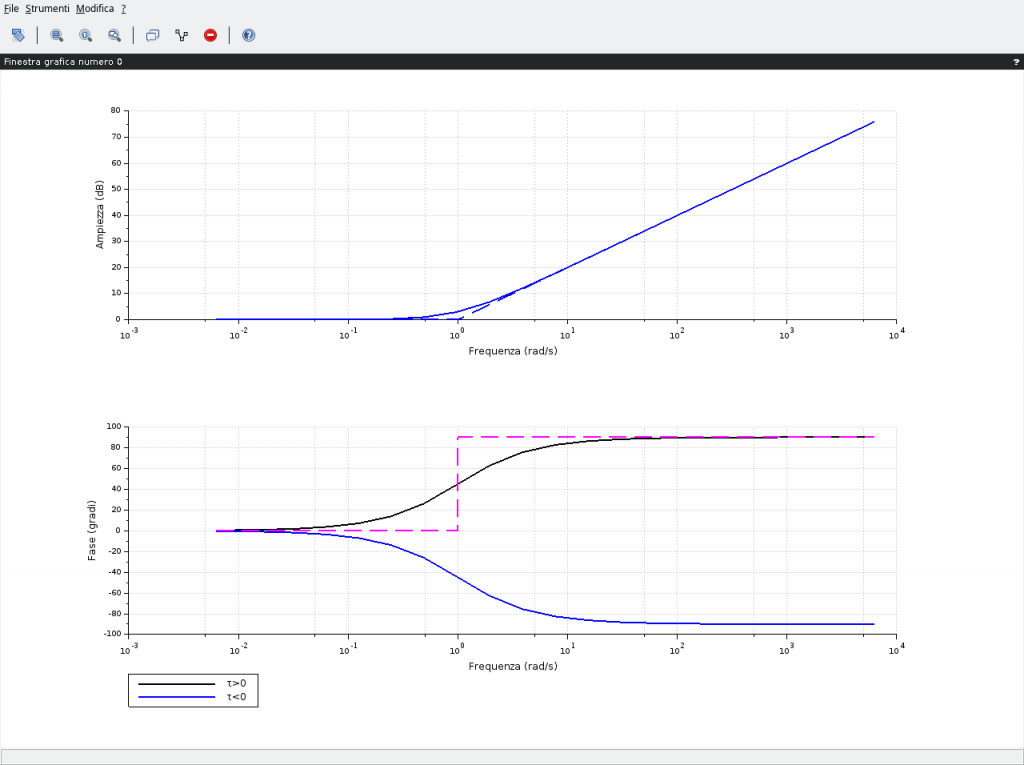
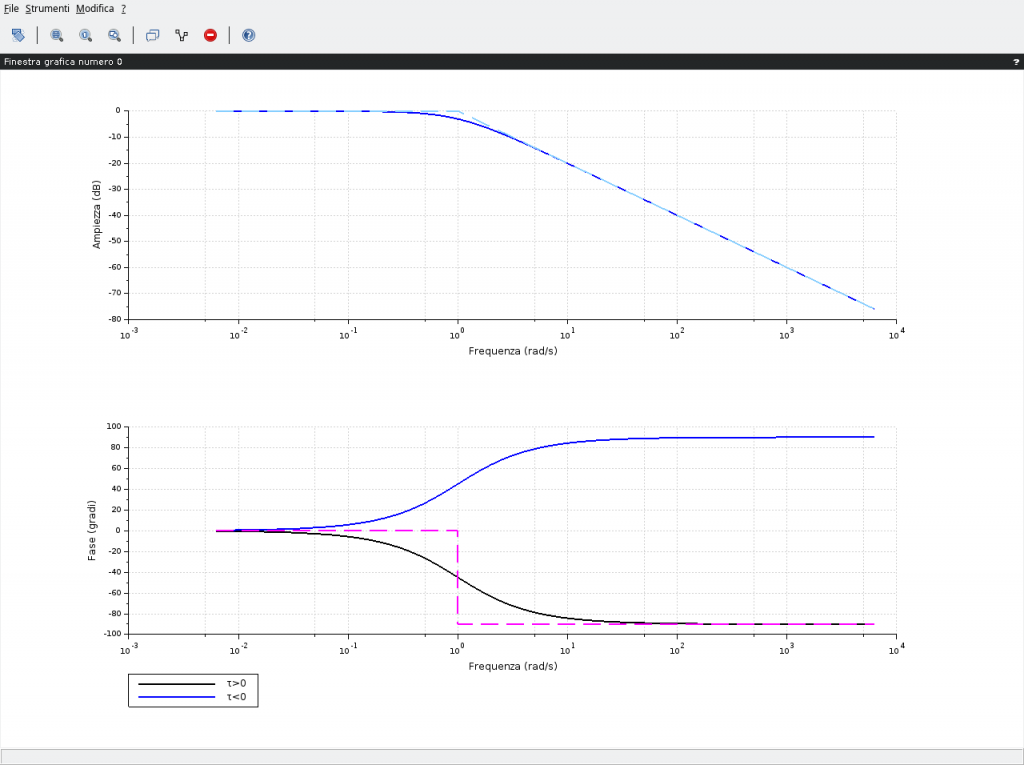
Gli andamenti di modulo e fase sono visibili in basso dove vengono evidenziati, in curve tratteggiate, anche gli andamenti asintotici. La differenza, come riportato nella legenda in basso nella stessa figura, riguarda solo il diagramma delle fasi poiché i moduli sono sovrapposti indipendentemente dal segno della costante di tempo.

La fase, invece, in presenza di costanti di tempo positive, quindi zeri nel semipiano sinistro del piano complesso, presenta un andamento indicato dalla curva in colore nero. Viceversa la presenza di costanti di tempo negative, allorquando gli zeri dovessero trovarsi nel semipiano di destra del piano complesso, originano la curva di colore blu.

 

Il diagramma in ambiente Scilab è possibile ottenerlo riportando il codice seguente nella console.

s=%s;
n=1+s;
d=1;
g=syslin('c',n,d);
num=1-s;
den=1;
h=syslin('c',num,den);
bode([g; h], ['τ>0'; 'τ<0'],"rad");bode_asymp([g]);

Il diagramma delle fasi può essere rappresentato anche con i cosiddetti diagrammi approssimati da spezzate costituito da 2 semirette orizzontali corrispondenti agli asintoti 0° e 90° e da un segmento obliquo. Quest’ultimo è ottenuto utilizzando una retta congiungente i punti 0° e 90° (per la curva nera) rispettivamente una decade prima e una decade dopo la pulsazione di rottura. Medesima considerazione per la curva in blu; una retta congiungente i punti 0° e -90°. In pratica una retta (un segmento di retta) che partendo da 0° una decade prima della pulsazione di rottura termina sul valore 90° una decade dopo la pulsazione di rottura. Ad esempio in figura per la curva nera essendo la pulsazione di rottura pari a 1rad/s la componente obliqua del diagramma a spezzate partirà dalle coordinate 0° e 0,1 rad/s e terminerà nel punto individuato dalle coordinate 90° e 10 rad/s e a partire da questi punti vanno aggiunte, rispettivamente, le rette orizzontali 0° e 90°.

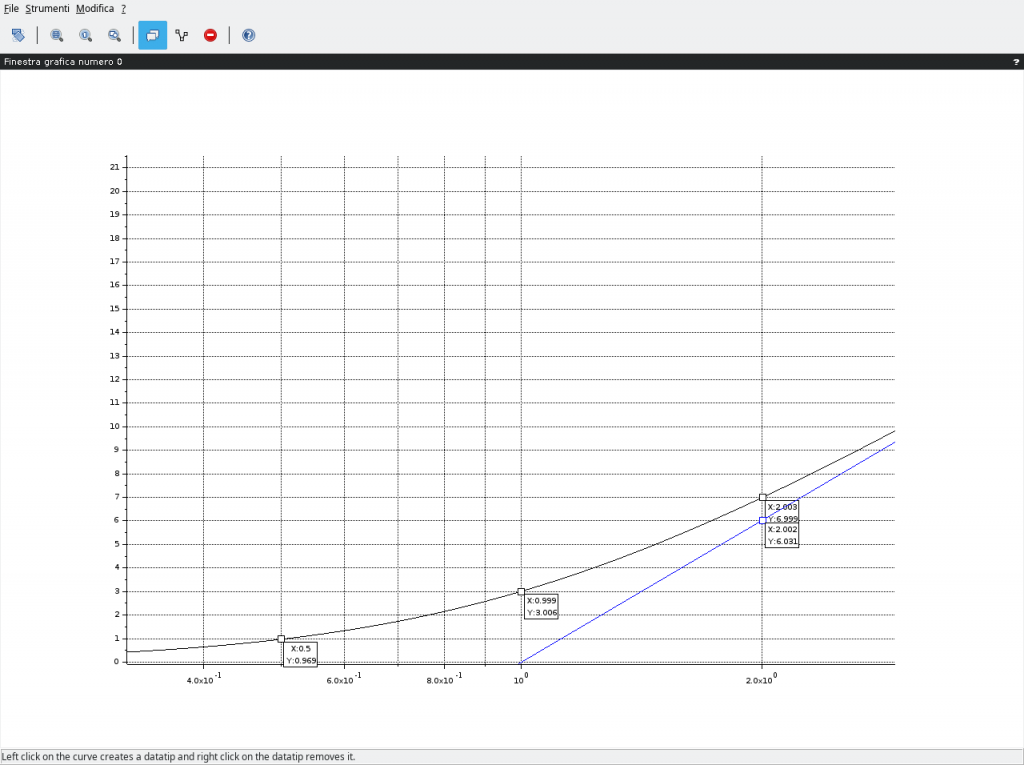
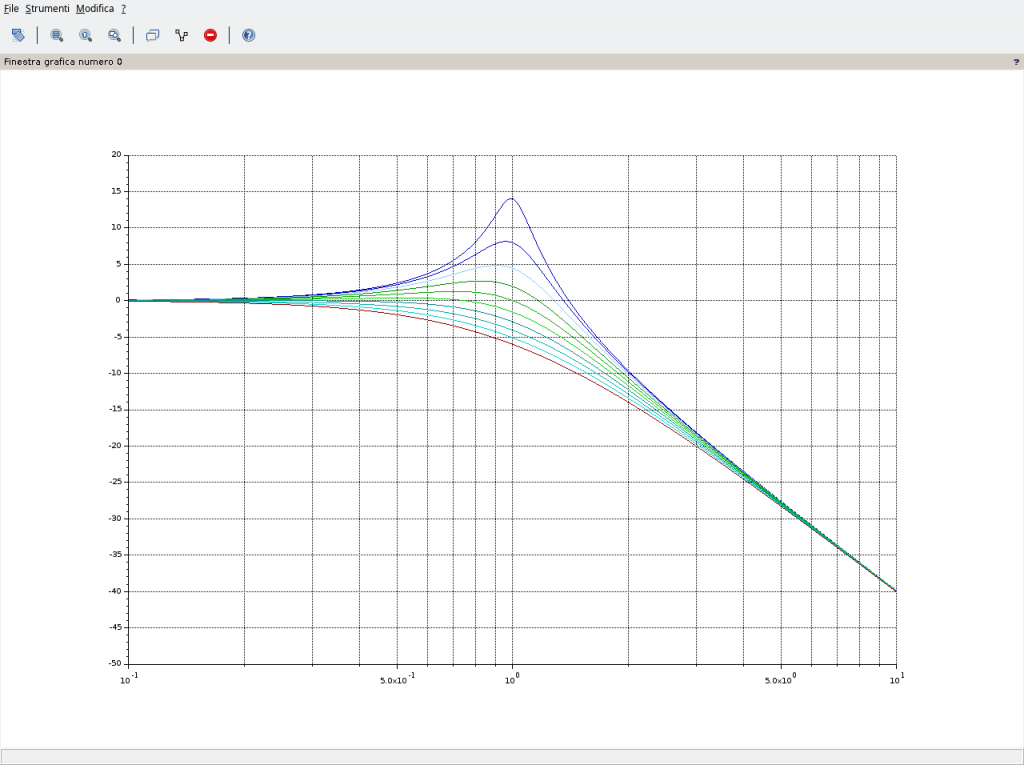
Altra interessante considerazione vede il calcolo dell’approssimazione tra il diagramma dei moduli reale (curva a tratto pieno in blu) e il corrispondente diagramma asintotico (curva a tratteggio medesimo colore). Se si provasse con Scilab a calcolare le differenze si otterrebbe quanto riportato nella figura in basso nella quale, in nero, viene riportato il diagramma reale e in blu il diagramma asintotico.

 

Dal punto di vista analitico è abbastanza semplice la valutazione dell’errore di approssimazione tra il disegnare un diagramma dei moduli asintotico rispetto ad un diagrammna reale. Infatti alla pulsazione di rottura risulta:

\omega=\omega^z=\frac{1}{\tau^z}: \left \{  \begin{array}{ll} |1+\jmath\omega^z\tau^z|_{dB}=20\log_{10}|1+\jmath|=20\log_{10}\sqrt{2}\eqsim3,010 \space\space [dB] \\ 0 \space\space [dB]\end{array} \right.

ovvero circa 3dB di differenza tra il diagramma reale e quello asintotico esattamente quanto riportato nella figura precedente. Con lo stesso criterio si può calcolare la differenza, ad esempio, al doppio della pulsazione di rottura ovvero a 2 rad/s il cui risultato vede:

\omega=2\omega^z=\frac{2}{\tau^z}: \left \{  \begin{array}{ll} |1+\jmath2\omega^z\tau^z|_{dB}=20\log_{10}|1+2\jmath|=20\log_{10}\sqrt{5}\eqsim6,989 \space\space [dB] \\ |\jmath2\omega^z\tau^z|_{dB}=20\log_{10}|2\jmath|=20\log_{10}2\eqsim6,021 \space\space [dB]\end{array} \right.

circa 6,021dB per il diagramma asintotico e 6,989dB per il diagramma reale determinando così un errore di approssimazione di circa 1dB esattamente come riportato nella figura precedente (a meno di frequenze di millesimi di Hz).

Con analogo procedimento si può valutare la differenza tra diagramma reale e asintotico alla metà della pulsazione di rottura:

\omega=\frac{\omega^z}{2}=\frac{1}{2\tau^z}: \left \{  \begin{array}{ll} |1+\jmath\frac{\omega^z\tau^z}{2}|_{dB}=20\log_{10}|1+\frac{\jmath}{2}|=20\log_{10}\frac{\sqrt{5}}{2}\eqsim0,969 \space\space [dB] \\ 0 \space\space [dB]\end{array} \right.

i cui risultati sono congruenti con quanto ottenuto con Scilab (e non potrebbe essere diversamente!).

Fattore binomio a denominatore (poli reali)

I diagrammi si ottengono per simmetria rispetto all’asse delle ascisse dai diagrammi degli zeri appena valutati. Una simulazione in Scilab fornisce:

 

Valgono le medesime considerazione sui diagrammi dei moduli e delle fasi effettuate per gli zeri reali.

Coppia di zeri complessi coniugati

Agli scenari fin qui descritti si aggiungono ulteriori due casi inerenti zeri e poli complessi coniugati, generalmente associati ad una equazione di secondo grado a coefficienti reali e positivi (teorema fondamentale dell’algebra) del tipo:

F(s)=a_0s^2+a_1s+a_2

le cui soluzioni si trovano facilmente imponendo la suddetta uguale a 0:

a_0s^2+a_1s+a_2=0 \Rightarrow s^2+\frac{a_1}{a_0}s+\frac{a_2}{a_0}=0

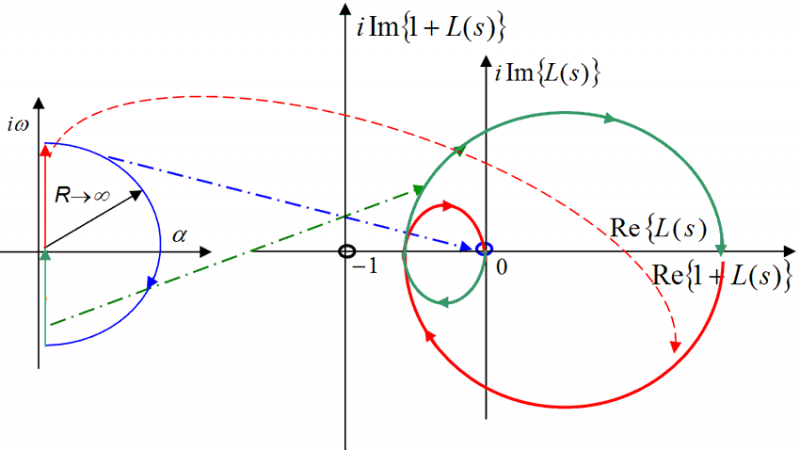
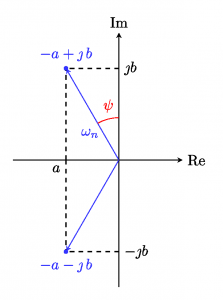Spesso, però, per la caratterizzazione di un modo pseudoperiodico si introducono due parametri come la pulsazione propria o naturale ω_n e lo smorzamento ξ . La posizione del punto complesso è univocamente determinato dalle coordinate del numero complesso che lo rappresenta. La lunghezza (modulo) del segmento che congiunge l’origine con il punto (coordinate del numero complesso) nel piano di Gauss definisce il valore della pulsazione naturale ω_n mentre il seno dell’angolo rispetto all’asse positivo immaginario determina il valore del fattore di smorzamento ξ in base all’immagine riportata di lato (un click per ingrandirla). Per le definizioni riportate, risulta:

\left \{  \begin{array}{ll} \omega_n=\sqrt{a^2+b^2}\\ \xi=\sin{\psi}=\frac{-a}{\sqrt{a^2+b^2}}=\frac{-a}{\omega_n} \end{array} \right. \kern{1cm}(7)

laddove a e b sono rispettivamente il coefficiente reale e il coefficiente immaginario del numero complesso rappresentato in figura. È evidente, poi, come dalle (7) sia possibile ricavarsi i coefficienti del complesso coniugato noti che siano i parametri ω_n e ξ, infatti:

\left \{  \begin{array}{ll} a=-\xi\omega_n \\ b=\omega_n \sqrt{1-\xi^2} \end{array} \right.

Una siffatta rappresentazione è stata implicitamente utilizzata nello sviluppo del termine j-esimo tra parentesi quadre nella (3) così come nella (5). Epurandolo di ogni apice e pedice, al fine di renderlo il più generico possibile, lo si può riscrivere come:

s^2+2\xi \omega_ns+\omega_n^2

La corrispondenza tra i parametri nelle due forme dell’equazione è abbastanza immediata:

\left \{  \begin{array}{ll} \omega_n^2=\frac{a_2}{a_0} \rightarrow \omega_n=\sqrt{\frac{a_2}{a_0}} \\ 2\xi\omega_n=\frac{a_1}{a_0} \rightarrow \xi=\frac{a_1}{2\sqrt{a_2a_0}} \end{array} \right.

Le soluzioni della equazione di secondo grado nella “seconda forma” forniscono la seguente rappresentazione:

s_{1,2}=\frac{-2\xi\omega_n\pm\sqrt{4\xi^2\omega_n^2-4\omega_n^2}}{2}=\frac{-2\xi\omega_n\pm\sqrt{4\omega_n^2(\xi^2-1)}}{2}=\\[1.5em]=\frac{-2\xi\omega_n\pm2\omega_n\sqrt{\xi^2-1}}{2}=-\xi\omega_n\pm\sqrt{\xi^2-1}=\\[1.5em]=\omega_n(-\xi\pm\sqrt{\xi^2-1})

per le quali in funzione del valore di ξ è possibile avere:

• |ξ|>1 radici reali e distinti;
• |ξ|=1 radici reali e coincidenti;
• |ξ|<1 radici complesse coniugate.

L’ultimo caso è quello di interesse poiché i primi due rientrano praticamente in quanto fin qui esaminato.

Riportando il termine nella forma di Bode come visibile, ad esempio, nella (5) dopo aver sostituito s=\jmath\omega per l’analisi nel dominio della frequenza, allora per una generica coppia di zeri è possibile scrivere:

1+2\xi^z\frac{s}{\omega_n^z}+\frac{s^2}{(\omega_n^z)^2}=1+2\xi^z\frac{\jmath\omega}{\omega_n^z}+\frac{(\jmath\omega)^2}{(\omega_n^z)^2}=1+2\xi^z\frac{\jmath\omega}{\omega_n^z}-\frac{\omega^2}{(\omega_n^z)^2}=\\[1.5em]=1-\frac{\omega^2}{(\omega_n^z)^2}+2\xi^z\frac{\jmath\omega}{\omega_n^z}\kern{1cm}(8)

Dalla (8) è evidente come risultino distinguibili la parte reale e la parte immaginaria e in quanto tale è possibile valutarne modulo e fase e il loro andamento al variare della pulsazione.

Per il modulo si può scrivere:

\left| 1-\frac{\omega^2}{(\omega_n^z)^2}+2\xi^z\frac{\jmath\omega}{\omega_n^z} \right|_{dB}\triangleq20\log_{10}\sqrt{\left(1-\frac{\omega^2}{(\omega_n^z)^2}\right)^2+4(\xi^z)^2\frac{\omega^2}{(\omega_n^z)^2}}=\\[1.5em]=10\log_{10}\left(\left(1-\frac{\omega^2}{(\omega_n^z)^2}\right)^2+4\xi^2\frac{\omega^2}{(\omega_n^z)^2}\right)\kern{1cm}(9)

Dalla (9) è possibile valutare l’andamento asintotico del modulo per valori della pusalzione da 0 tendenti all’infinito. Suddividiamo l’analisi in due percorsi differenti.

Alle basse frequenze, quindi per \omega\rightarrow0^+\Longleftrightarrow\omega\ll\omega_n, dalla (9) è evidente come risulti 10\log_{10}(1)=0dB, quindi un andamento assimilabile ad una retta coincidente con l’asse delle ascisse. O meglio, l’asse delle ascisse ne è l’asintoto.

Di contro alle alte frequenze \omega\rightarrow\infty\Longleftrightarrow\omega\gg\omega_n il termine trinomio è possibile riscriverlo, considerando il primo membro della (9), il risultato della stessa (9) e ricordando le proprietà dei logaritmi:

\left| 1-\frac{\omega^2}{(\omega_n^z)^2}+2\xi^z\frac{\jmath\omega}{\omega_n^z} \right|_{dB}\eqsim\left|-\frac{\omega^2}{(\omega_n^z)^2}\right|_{dB} \triangleq 20\log_{10}\sqrt{\left(\frac{\omega^2}{(\omega_n^z)^2} \right)^2}=\\[1.5em]=20\log_{10}\frac{\omega^2}{(\omega_n^z)^2}=20\log_{10}\left(\frac{\omega}{\omega_n^z}\right)^2=40\log_{10}\left(\frac{\omega}{\omega_n^z}\right)=\\[1.5em]=40\log_{10}(\omega)-40\log_{10}(\omega_n^z)

la cui soluzione identifica l’equazione di una retta con pendenza 40db/decade, equazione che per una maggiore comprensione può essere riscritta:

y=40x-40\log_{10}(\omega_n^z)

Le due spezzate che identificano il diagramma asintotico in presenza di zeri complessi coniugati si incontrano nel punto y=0 ovvero per 0=40x-40\log_{10}(\omega_n^z) e quindi in:

x=\log_{10}(\omega_n^z)\rightarrow\omega=\omega_n^z

Va da se come un siffatto diagramma presenti inevitabilmente degli scostamenti rispetto al diagramma effettivo i cui valori sono funzioni di ξ. Infatti per valori della pulsazione pari alla pulsazione naturale (di rottura) dello zero risulta, partendo dal primo membro della (9):

\left| 1-\frac{\omega^2}{(\omega_n^z)^2}+2\xi^z\frac{\jmath\omega}{\omega_n^z} \right|_{dB \space \omega=\omega_n^z}=\left| \cancel{1}-\cancel{\frac{(\omega_n^z)^2}{(\omega_n^z)^2}}+2\xi^z\frac{\jmath\omega_n^z}{\omega_n^z} \right|_{dB}=\\[1.5em]=20\log_{10}2|\xi^z| \left \{  \begin{array}{ll} 20\log_{10}(2)\eqsim6,021dB \Longleftrightarrow |\xi^z|=1 \\ 20\log_{10}(2*0,707)\eqsim3,009dB \Longleftrightarrow |\xi^z|=0,707  \\ 20\log_{10}(2*0,5)=0dB \Longleftrightarrow |\xi^z|=0,5 \\ 20\log_{10}(2*0,1)\eqsim-13,979dB \Longleftrightarrow |\xi^z|=0,1 \\ 20\log_{10}(0)\rightarrow\ -\infty \Longleftrightarrow \xi^z=0 \end{array} \right.

dai quali si evince come l’approssimazione aumenti per ξ→0. In più si osserva come per ξ=0 – coppia di zeri puramente immaginari – si ha un asintoto a -∞ per ω→ω^z_n il che significa che il modulo di un fattore trinomio a numeratore ha un picco negativo (antirisonanza o attenuazione) in prossimità della pulsazione naturale e il suddetto valore è tanto più accentuato quanto minore è il coefficiente di smorzamento ξ.

Come noto dallo studio delle funzioni, il punto di minimo della curva fornirà lo scostamento massimo. Ma la curva in oggetto può presentare un punto di minimo se esiste un valore reale della pulsazione ω tale da annullare la derivata prima del termine trinomio della risposta armonica, ovvero la derivata dell’argomento della (9). Ricordando la formula di derivazione di funzioni di funzioni risulta, per una generica coppia di zeri complessi coniugati:

\frac{d}{d\omega}\left(\left(1-\frac{\omega^2}{(\omega_n^z)^2}\right)^2+4(\xi^z)^2\frac{\omega^2}{(\omega_n^z)^2}\right)=\\[1.5em]=2\left(1-\frac{\omega^2}{(\omega_n^z)^2}\right)\left(-2\frac{\omega}{(\omega_n^z)^2}\right)+8(\xi^z)^2\frac{\omega}{(\omega_n^z)^2}=0

Sviluppando i semplici calcoli algebrici si arriva alla soluzione:

\omega_R=\omega_n^z\sqrt{1-2(\xi^z)^2}\kern{1cm}(10)

che comporta la presenza di un valore reale della pulsazione se e solo se il termine sotto radice quadrata risulta essere maggiore di 0. La pulsazione ω_R viene detta pulsazione di risonanza e coincide con il valore della pulsazione naturale solo quando ξ^z=0. Per tutti gli altri valori, |\xi^z|\lt\frac{\sqrt{2}}{2} ricavato subito in basso, è evidente come risulti ω_R<ω^z_n e quindi nell’andamento del modulo sarà chiaro il motivo per cui la pulsazione di risonanza si trova sempre a sinistra della pulsazione di rottura.

Imporre valori reali della pulsazione di risonanza implica, dalla (10), che ciò potrà avvenire solo per determinati valori del fattore di smorzamento ξ. Infatti dovendo essere 1-2(\xi^z)^2\gt0, allora risulta:

2(\xi^z)^2\lt1 \rightarrow (\xi^z)^2\lt\frac{1}{2} \rightarrow |\xi^z|\lt\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\eqsim 0,707\kern{1cm}(11)

Ai valori reali della pulsazione di risonanza è possibile valutare il modulo della risposta armonica, per tale motivo definito modulo alla risonanza rapporto tra il massimo valore del modulo assunto dalla funzione di risposta armonica e il valore dello stesso per ω=0, lo si calcola facilmente sostituendo nella (9) la (10):

|M_R|_{dB \space\space \omega=\omega_R}=20\log_{10}\sqrt{\left(1-\frac{\omega_R^2}{(\omega_n^z)^2}\right)^2+4(\xi^z)^2\frac{\omega_R^2}{(\omega_n^z)^2}}=\\[1.5em]=20\log_{10}\sqrt{\left(1-\frac{\cancel{(\omega_n^z)^2}(1-2(\xi^z)^2)}{\cancel{(\omega_n^z)^2}}\right)^2+4(\xi^z)^2\frac{\cancel{(\omega_n^z)^2}(1-2(\xi^z)^2)}{\cancel{(\omega_n^z)^2}}}=\\[1.5em]=20\log_{10}\sqrt{(\cancel1-\cancel1+2(\xi^z)^2)^2+4(\xi^z)^2(1-2(\xi^z)^2)}=\\[1.5em]=20\log_{10}\sqrt{4(\xi^z)^4+4(\xi^z)^2(1-2(\xi^z)^2)}=20\log_{10}\sqrt{4(\xi^z)^4+4(\xi^z)^2-8(\xi^z)^4}=\\[1.5em]=20\log_{10}\sqrt{4(\xi^z)^4+4(\xi^z)^2-8(\xi^z)^4}=20\log_{10}\sqrt{4(\xi^z)^2-4(\xi^z)^4}=\\[1.5em]=20\log_{10}\sqrt{4(\xi^z)^2(1-(\xi^z)^2)}

in definitiva:

|M_R|_{dB \space\space \omega=\omega_R}=20\log_{10}2|\xi^z|\sqrt{1-(\xi^z)^2}\kern{1cm}(12)

e per i valori di ξ indicati (per i quali si ha una pulsazione reale) la risposta del sistema è detta risonante (o sottosmorzata). In tutti gli altri casi si ha una risposta sovrasmorzata (o non risonante).

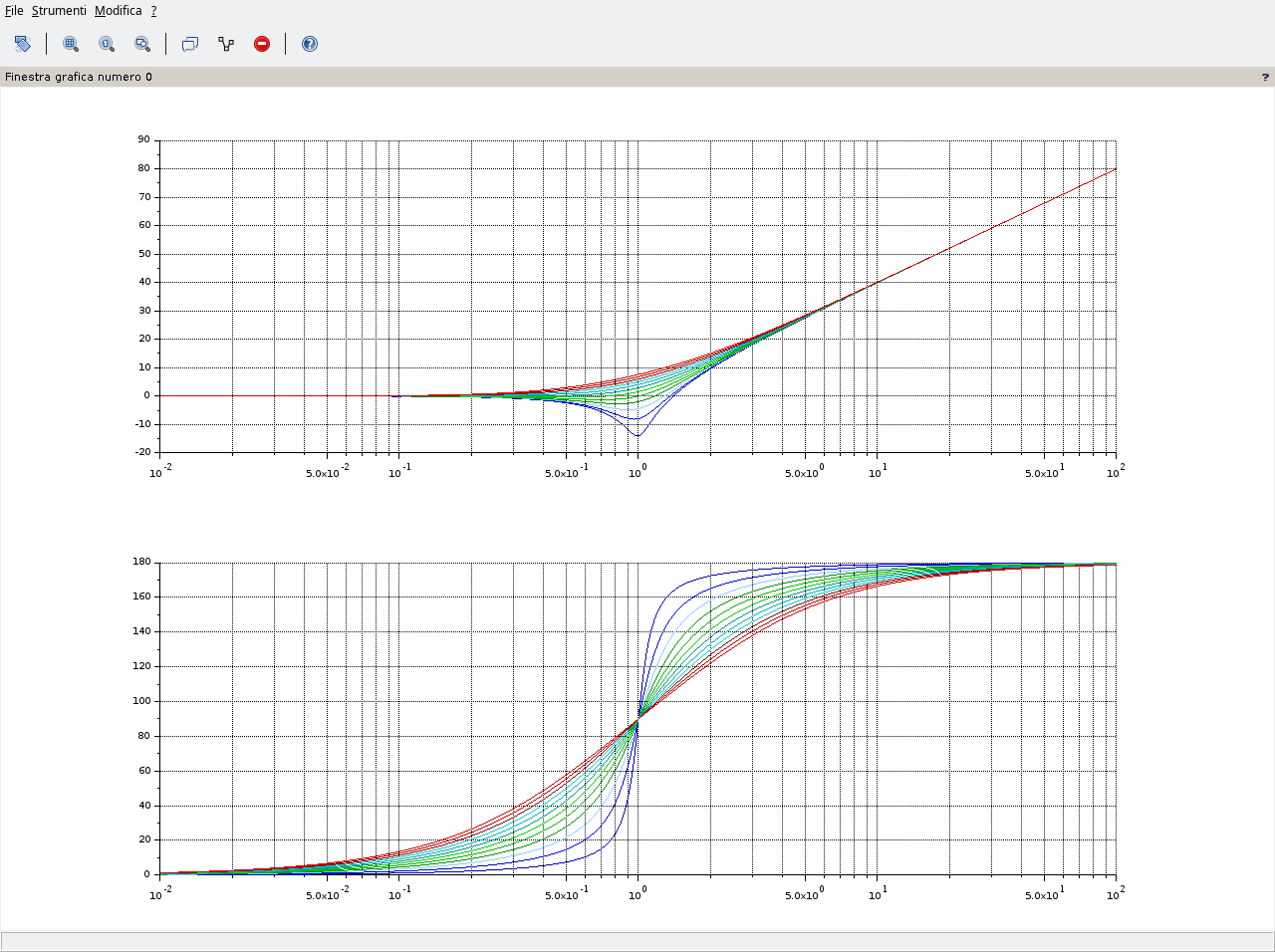
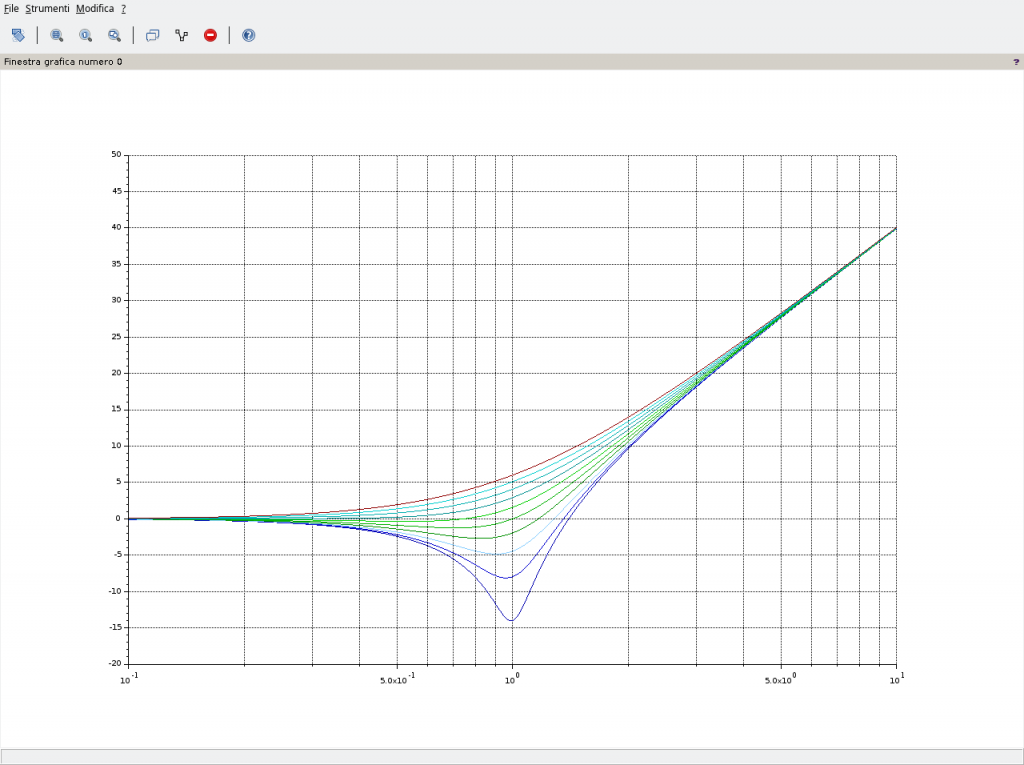
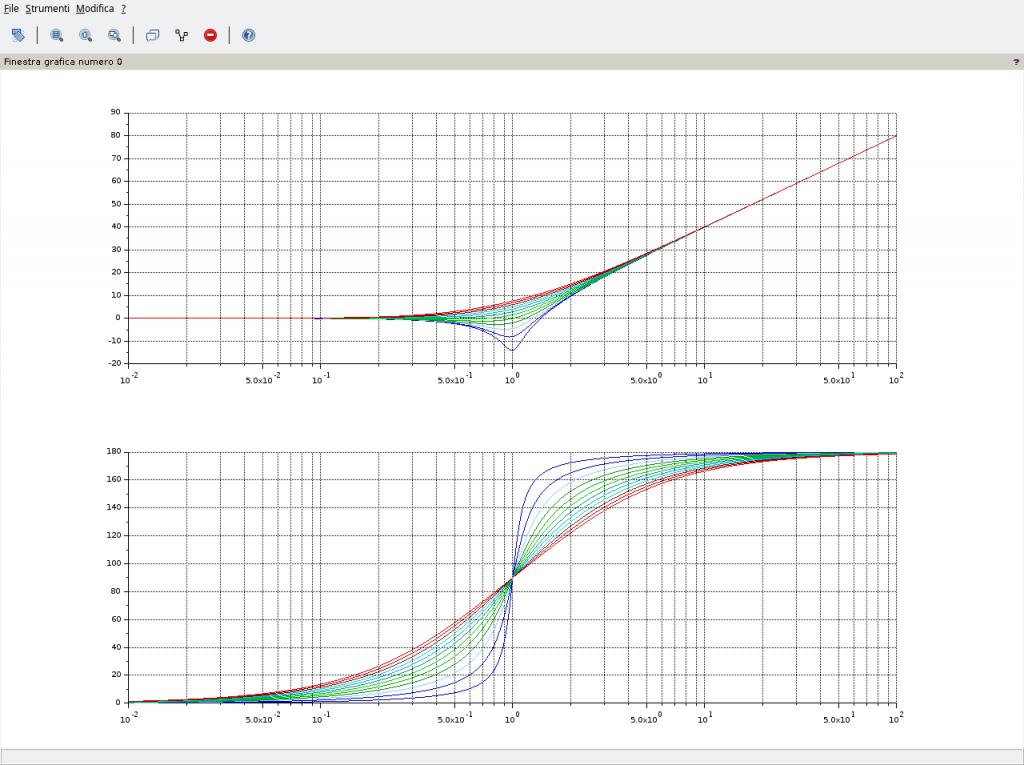
Quanto fin qui riportato giustifica l’andamento del diagramma dei moduli, di seguito riportato utilizzando Scilab e nel quale il parametro è il fattore di smorzamento ξ.

 

Notare la prima curva in alto relativa a poli reali e coincidenti, ovvero ξ=1, il cui grafico presenta una pendenza di 40dB/decade. In presenza di zeri complessi coniugati a molteplicità maggiori di 1 la pendenza va moltiplicata per la molteplicità. Così qualora si avesse una coppia di zeri complessi coniugati a molteplicità 2 la pendenza del grafico raddoppierebbe passando da 40dB/decade a 80dB/decade.

L’andamaneto del modulo appena riportato lo si può ottenere utilizzando il seguente sorgente – che è possibile migliorare/modificare a proprio piacimento – da salvare su un file con estensione .sce, da aprirsi con SciNotes e  lanciarlo utilizzando la classica icona di “play”. In questo esempio viene impostato ω_n=1 con ξ come parametro variabile da 0,1 fino a 1 a passi di 0,1.

colore=10;
w=logspace(-1,1,10000);
wn=1;
s=%i*w
for xi=0.1:0.1:1
    num=poly([wn 2*xi*wn 1],'s','c')
    den=poly([1 0 0],'s','c');
    F1jw=horner(num,%i*w)./horner(den,%i*w);
    modF1jw=20*log10(abs(F1jw));
    plot2d(w,F1jw',logflag='ln'),xgrid
    colore_linea = gce();
    colore_linea.children.foreground = colore;
    colore=colore+1;
end

 

A questo punto rimane da riportare il grafico della fase del termine trinomio in presenza di zeri complessi coniugati Il punto di partenza è sempre la (8) che riscritta per un generico zero risulta (senza utilizzare pedici così si evita di appesantire ulteriormente la notazione):

\phase{1-\frac{\omega^2}{\omega_n^2}+2\xi\frac{\jmath\omega}{\omega_n}}=\arctg\left(\frac{2\xi\frac{\omega}{\omega_n}}{\left( 1-\frac{\omega^2}{\omega_n^2} \right)}\right)\kern{1cm}(13)

È opportuno seguire la stessa modalità vista per l’andamento dei moduli; suddividere l’analisi in bassa frequenza e in alta frequenza distinguendo tra ξ>0 e ξ<0.

Per 0≤ξ≤1 alle basse frequenze, ovvero \omega\rightarrow0^+\Longleftrightarrow\omega\ll\omega_n, dalla precedente è immediato dedurre come l’argomento dell’arcotangente tenda a 0 pertanto la fase tende a 0°.

Per il medesimo range di valori del fattore di smorzamento, ad esclusione di ξ=0, quando il valore della pulsazione eguaglia il valore della pulsazione di rottura il sottraendo a denominatore tende a 1 da valori minori di 1 pertanto lo stesso denominatore tende a 0 da valori positivi. Questo comporta che l’argomento tende ad infinito, ed essendo:

\lim_{x\to\infty} \arctg(x)=\frac{\pi}{2}

implica che al valore della pulsazione di rottura ω_n il diagramma della fasi vale +π/2.

Infine, alle alte frequenze \omega\rightarrow\infty\Longleftrightarrow\omega\gg\omega_n, sempre per 0≤ξ≤1, è evidente come nel termine trinomio prevalga la componente quadratica pertanto per valori della pulsazione molto alta (al limite tendente ad infinito) può essere scritto come:

{1-\frac{\omega^2}{\omega_n^2}+2\xi\frac{\jmath\omega}{\omega_n}}|_{\omega\rightarrow\infty}\eqsim -\frac{\omega^2}{\omega_n^2}

e l’argomento di un numero reale negativo è pari a π. Ritenuto positivo poiché, per valori della pulsazione che crescono da 0 verso infinito, il corrispondente vettore del numero complesso presenta sempre un valore positivo della parte immaginaria – primo e secondo quadrante – passando dal valore positivo a negativo della parte reale nel punto ω=ω_n (valore della fase +π/2) ruotando così in senso antiorario e “adagiandosi”, all’aumentare in proporzione del valore della parte reale rispetto alla corrispondente parte immaginaria, sull’asse reale negativo. In conclusione una rotazione antioraria pari a +π.

Tutto questo per valori positivi del fattore di smorzamento per valori negativi, ovvero -1≤ξ≤0, i diagrammi dei moduli rimangono inalterati mentre i diagrammi delle fasi si ribaltano in maniera simmetrica rispetto all’asse delle ascisse.

Riassumendo:

\phase{1-\frac{\omega^2}{\omega_n^2}+2\xi\frac{\jmath\omega}{\omega_n}}=\left \{  \begin{array}{ll} 0 \space\space \omega\rightarrow0 \\ \frac{\pi}{2}\times segno(\xi) \space\space \omega\rightarrow\omega_n \\ \pi \times segno(\xi) \space\space \omega\rightarrow\infty \end{array} \right.

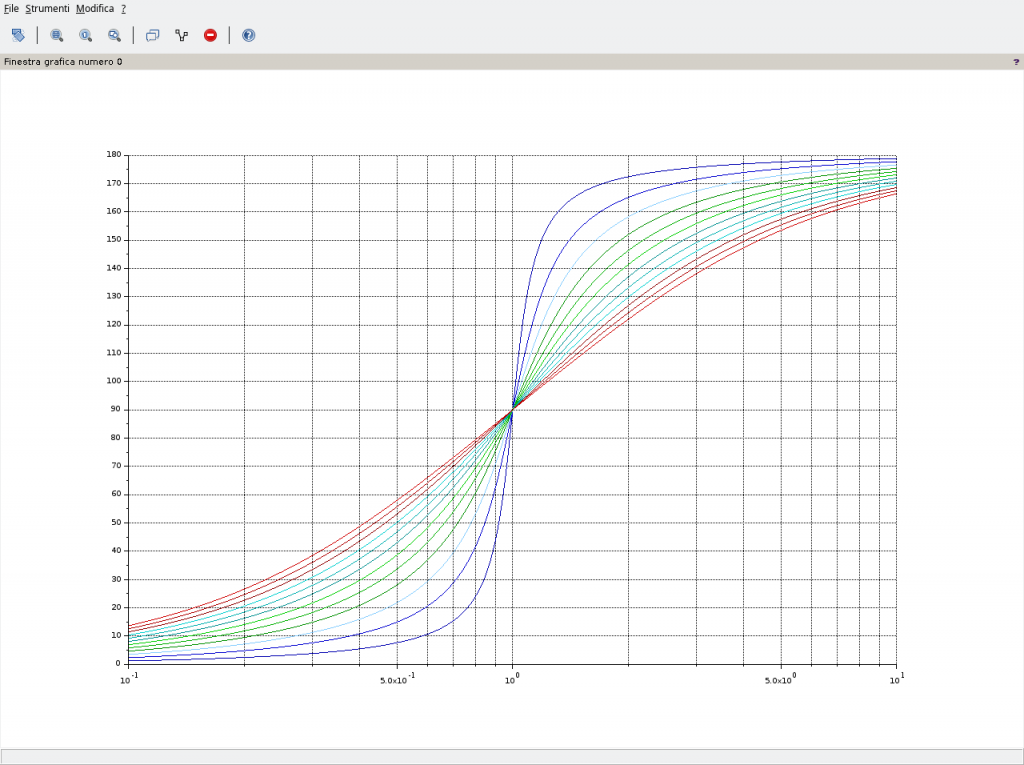
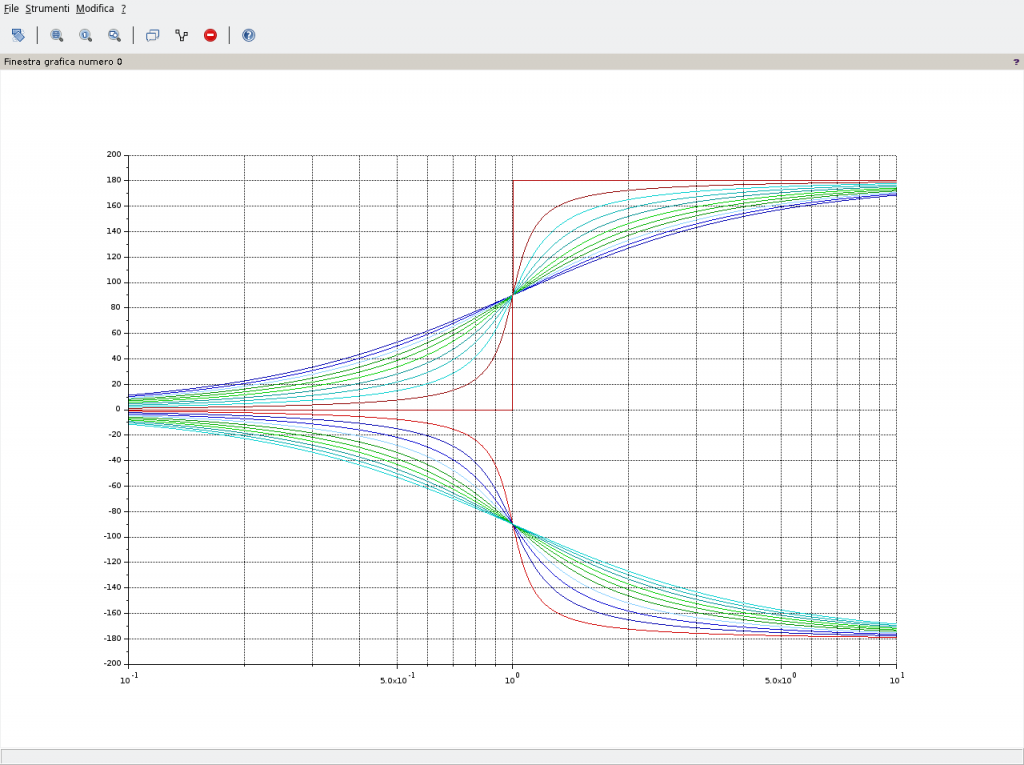
Per valori positivi del fattore di smorzamento:

 

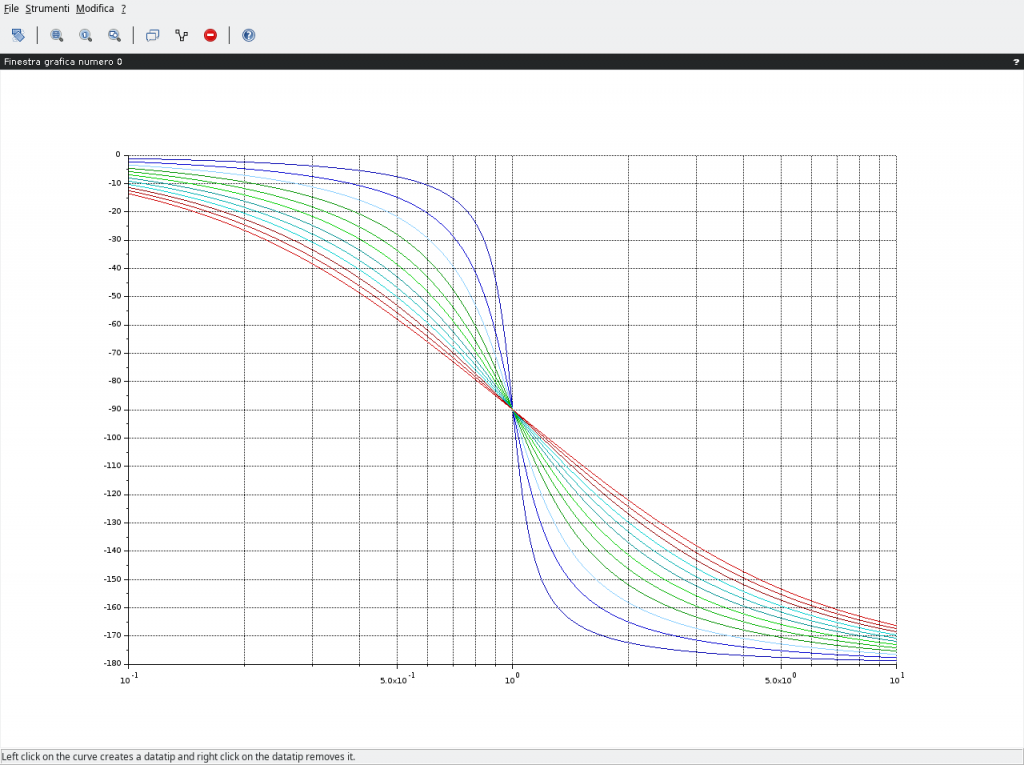
mentre per valori negativi (diagrammi mantenuti separati al fine di evitare confusione):

 

L’interpretazione dell’andamento è intuitiva. Fissata una coppia di numeri complessi coniugati, soluzione della risposta armonica della (8), allora nella fase, visibile nella (13), al variare di ξ varia solo il coefficiente immaginario del numero complesso, la parte reale rimane la stessa. Nel piano di Gauss questo implica che il corrispondente numero complesso presenta una fase maggiore ovvero, a parità di pulsazione e.g. 2rad/s, la curva a ξ maggiore si trova al di sotto di quella a ξ minore perché solo così nel diagramma delle fasi la fase può essere maggiore.

Per ottenere i diagrammi delle fasi con Scilab è sufficiente aggiungere la riga e modificare la plot2d nel modo riportato.

faseF1jw=phasemag(F1jw);
plot2d(w,faseF1jw',logflag='ln'),xgrid

Comunque è sempre possibile riportare entrambi i diagrammi dei moduli e delle fasi (e.g. per fattore di smorzamento positivo) nella stessa finestra a colori corrispondenti:

 

Il sorgente Scilab, file .sce, si modifica sensibilmente nel modo che segue (è solo uno snippet, ognuno è libero di modificarlo/migliorarlo come meglio crede):

colore=10;
w=logspace(-2,2,10000);
wn=1;
s=%i*w
for xi=0.1:0.1:1.2
    num=poly([wn 2*xi*wn 1],'s','c')
    den=poly([1 0 0],'s','c');
    F1jw=horner(num,%i*w)./horner(den,%i*w);
    modF1jw=20*log10(abs(F1jw));
    faseF1jw=phasemag(F1jw);
    subplot(211),plot2d(w,modF1jw',logflag='ln'),xgrid
    colore_linea_mod = gce();
    colore_linea_mod.children.foreground = colore;
    subplot(212),plot2d(w,faseF1jw',logflag='ln'),xgrid
    colore_linea_fase = gce();
    colore_linea_fase.children.foreground = colore;
    colore=colore+1;
end

 

 

Coppia di poli complessi coniugati

Non deve far sorprendere se una coppia di poli complessi coniugati presenta un comportamento similare ad una coppia di zeri complessi coniugati. Per quanto ne attiene l’andamento del diagramma dei moduli si ha un comportamento simmetrico alla coppia di zeri complessi coniugati:

 

dove è evidente come a differenza dei poli in presenza del modulo alla risonanza alla pulsazione di risonanza ω_n non si ha più una attenuazione bensì una amplificazione (comportamento risonante) funzione del valore del fattore di smorzamento ξ a cui fa seguito una pendenza di -40dB/decade. Con Scilab questo andamento è ottenibile dal precedente listato semplicemente elevando il numeratore a -1. In presenza di molteplicità il suddetto diagramma aumenta la propria pendenza in misura proporzionale, i.e. in caso di poli complessi coniugati di molteplicità 2 la pendenza sarà di -80dB/decade.

La dimostrazione è semplice. Il punto di partenza può essere la (8) elevata a -1 perché ora è a denominatore, ovvero, ricordando le proprietà elementari dei logaritmi:

\left| \left(1-\frac{\omega^2}{(\omega_n^p)^2}+2\xi^p\frac{\jmath\omega}{\omega_n^p} \right)^{-1} \right|_{dB}\triangleq20\log_{10}\frac{1}{\sqrt{\left(1-\frac{\omega^2}{(\omega_n^p)^2}\right)^2+4(\xi^p)^2\frac{\omega^2}{(\omega_n^p)^2}}}=\\[1.5em]=-20\log_{10}\sqrt{\left(1-\frac{\omega^2}{(\omega_n^p)^2}\right)^2+4(\xi^p)^2\frac{\omega^2}{(\omega_n^p)^2}}

Seguendo lo stesso criterio visto per zeri complessi coniugati alle basse frequenze, per ω→0⁺, dalla precedente si evince -20\log_{10}(1)=0. Risultato, asse delle ascisse è l’asintoto.

Alle alte frequenze, quindi per ω→∞ ovvero ω»ω_n, il termine sotto radice, analogamente a quanto fatto per gli zeri complesso coniugati, è possibile approssimarlo al solo termine quadratico:

\left(1-\frac{\omega^2}{(\omega_n^p)^2}\right)^2+4(\xi^p)^2\frac{\omega^2}{(\omega_n^p)^2}\eqsim\left(\frac{\omega^2}{(\omega_n^p)^2}\right)^2

il che comporta:

|F(\jmath\omega)|_{dB}=-20\log{10}\left(\frac{\omega}{\omega_n^p}\right)^2=-40\log_{10}\left(\frac{\omega}{\omega_n^p}\right)=\\[1.5em]=-40\log_{10}\omega+40\log_{10}\omega_n^p

ovvero, con analogo ragionamento visto per la coppia di zeri complessi coniugati, una retta con pendenza -40dB/decade ed è ovvio come tale diagramma presenti inevitabilmente degli scostamenti rispetto al diagramma reale, discostamenti funzioni di ξ e di valore uguali, al netto del segno, agli scostamenti già calcolati per zeri complessi coniugati. Questa volta il risultato è una risonanza – con annessa amplificazione funzione di ξ – in prossimità della pulsazione di risonanza e il cui valore, con procedimento analogo, è pari a:

F(\jmath\omega)|_{dB \space \omega=\omega_n}=-20\log_{10}2|\xi^p|

Anche per poli complessi coniugati, dallo studio delle funzioni, il massimo della curva fornirà lo scostamento massimo. Ma nel diagramma dei moduli il massimo valore corrisponde alla presenza di un minimo nella funzione:

20\log_{10}\frac{1}{\sqrt{\left(1-\frac{\omega^2}{(\omega_n^p)^2}\right)^2+4(\xi^p)^2\frac{\omega^2}{(\omega_n^p)^2}}}

il che, che è lo stesso, nella presenza di un minimo nella funzione sotto il segno di radice al denominatore. Tale minimo lo si può valutare imponendo a 0 la derivata prima della suddetta funzione:

\frac{d}{d\omega}\left[ \left(1-\frac{\omega^2}{(\omega_n^p)^2}\right)^2+4(\xi^p)^2\frac{\omega^2}{(\omega_n^p)^2} \right]=0

Con procedimento analogo alla coppia di zeri complessi coniugati si trova che:

\omega_R=\omega_n^p\sqrt{1-2(\xi^p)^2}

che comporta la presenza di un valore reale della pulsazione se e solo se il termine sotto radice quadrata risulta essere maggiore di 0. La pulsazione ω_R è, ovviamente, la pulsazione di risonanza e coincide con il valore della pulsazione naturale solo quando ξ=0. Per gli altri valori del fattore di smorzamento |\xi|\lt\frac{\sqrt{2}}{2} per i quali la pulsazione è reale, risulta ω_R<ω_n che giustifica l’andamento del grafico del diagramma dei moduli per il quale la pulsazione di risonanza è sempre a sinistra della pulsazione di rottura.

Al valore della pulsazione di risonanza è possibile valutare il modulo alla risonanza M_R per una coppia di poli complessi coniugati, valore che in dB vale, previa sostituzione della precedente ω_R:

|M_R|_{dB \space\space \omega=\omega_R}=20\log_{10}\frac{1}{\sqrt{\left(1-\frac{\omega_R^2}{(\omega_n^p)^2}\right)^2+4(\xi^p)^2\frac{\omega_R^2}{(\omega_n^p)^2}}}=\\[1.5em]=20\log_{10}\frac{1}{\sqrt{\left(1-\frac{\cancel{(\omega_n^p)^2}(1-2(\xi^p)^2)}{\cancel{(\omega_n^p)^2}}\right)^2+4(\xi^p)^2\frac{\cancel{(\omega^p)^2}(1-2(\xi^p)^2)}{\cancel{(\omega_n^p)^2}}}}=\\[1.5em]=20\log_{10}\frac{1}{\sqrt{4(\xi^p)^4+4(\xi^p)^2-8(\xi^p)^4}}

che fornisce come risultato, dopo un paio di semplici passaggi algebrici:

|M_R|_{dB \space\space \omega=\omega_R}=\frac{1}{2|\xi^p|\sqrt{1-(\xi^p)^2}}

Per l’andamento del diagramma delle fasi è sufficiente considerare:

\phase{\frac{1}{1-\frac{\omega^2}{\omega_n^2}+2\xi\frac{\jmath\omega}{\omega_n}}}=-\arctg\left(\frac{2\xi\frac{\omega}{\omega_n}}{\left( 1-\frac{\omega^2}{\omega_n^2} \right)}\right)

e seguendo lo stesso ragionamento visto per una coppia di zeri complessi coniugati è evidente come i diagrammi delle fasi risultino “invertiti” rispetto a coppie di zeri complessi coniugati. Nella figura che segue – ottenuta con semplici modifiche del listato precedente – in alto sono visibili gli andamenti per fattore di smorzamento negativo (compreso il valore 0) e in basso l’andamento del diagramma delle fasi quando il fattore di smorzamento assume valori positivi.