Criterio di stabilità di Nyquist
La stabilità di un sistema a catena chiusa può essere valutata calcolando i poli della funzione di trasferimento (f.d.t.) a catena chiusa oppure analizzando, previo uso del criterio di Routh (se il polinomio non ha un grado elevato), i segni della loro parte reale.
Queste tipiche metodologie (non sono le uniche) sebbene siano valide per l’analisi della stabilità, forniscono poca o nessuna percezione sulla robustezza della stabilità del sistema di controllo (e controllato) così come alcuna informazione viene ottenuta sull’influenza delle scelte progettuali.
Per tale motivo si ha la assoluta necessità di un qualche criterio di analisi basato sulla risposta in frequenza del sistema che permetta di avere immediatamente utili indicazioni sulla sintesi del controllore e sul comportamento del sistema nel suo complesso. A tal proposito viene in soccorso il criterio di Nyquist basato su quello che verrà definito il diagramma di Nyquist il quale permette anche di definire, seppur qualitativamente, dei margini di stabilità attraverso i quali capire di quanto il sistema è lontano dall’instabilità o dalla stabilità in presenza di un sistema instabile.
Indice - Table of Contents
Criterio di stabilità di Nyquist
Il criterio di Nyquist è relativo allo studio della stabilità di un sistema a retroazione e può essere visto come la “spina dorsale” dei metodi della risposta in frequenza. Il criterio lega tra loro le proprietà del sistema ad anello aperto e del sistema ad anello chiuso, in particolare fornisce informazioni sulla stabilità di un sistema ad anello chiuso a partire da alcune proprietà note del sistema ad anello aperto.
In tale scenario si vedrà a breve come l’applicazione consista in una formula fondamentale, solo apparentemente “banale”, e applicabile senza alcuna ipotesi particolare. La formula non è stata sviluppata da Nyquist ma è una conseguenza dello studio delle funzioni complesse, il fisico svedese Harry Theodor Nyquist ne intuì una notevole applicazione grafica che va sotto il nome di diagramma di Nyquist.
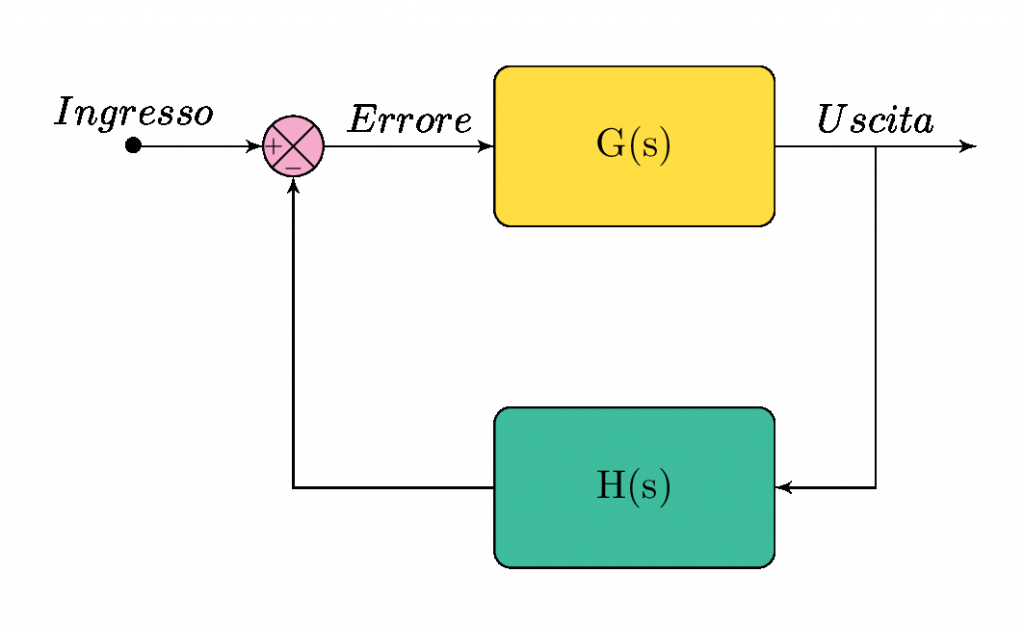
Dato un usuale sistema in retroazione come visibile nella figura in alto, è noto (Teoria dei Sistemi) come la funzione di trasferimento ad anello chiuso possa essere scritta, ragionando in termini di trasformata di Laplace delle grandezze/blocchi in essere:
\frac{U(s)}{I(s)}=\frac{G(s)}{1+G(s)H(s)}\kern{1cm}(1)
in base alla quale se non esiste una soluzione nell’RHP (Right-Half Plane, semipiano destro, zona grigia immagine in basso) del piano S, asse immaginario incluso, allora il sistema ad anello chiuso è stabile asintoticamente. Il prodotto a denominatore G(s)H(s) è definito guadagno di anello, ed è proprio su questo termine che può essere applicato il criterio di stabilità secondo Nyquist.

Per l’algebra degli schemi a blocchi vale la pena ricordare come un sistema che presenti un blocco nella catena di reazione è sempre possibile ricondurlo ad un sistema a retroazione unitaria del tutto equivalente, ad esempio per il precedente sistema:

Le funzioni G(s), funzione di trasferimento del processo da controllare, e H(s), funzione di trasferimento dell’elemento nell’anello di reazione (e.g. sensore, rete di reazione RC ecc) sono in generale delle funzioni note e tali da fornire un rapporto di polinomi del tipo:
G(s)H(s)=F(s)=\frac{N_F(s)}{D_F(s)}
per il quale è possibile definire:
- NF(s), il polinomio degli zeri del prodotto delle funzioni di trasferimento G(s)H(s);
- DF(s), il polinomio dei poli del prodotto delle funzioni di trasferimento G(s)H(s).
Nella rappresentazione nello spazio di stato la funzione ad anello aperto G(s)H(s)=F(s) assume una forma del tipo:
\left \{ \begin{array}{ll} \dot{x}=Ax+Bu\\y=Cx \end{array} \right.
Nel momento in cui viene chiuso l’anello di reazione è evidente come l’ingresso di errore al blocco G(s)H(s)=F(s) sia pari al valore di riferimento sottratto il valore di uscita (retroazione negativa) ovvero u=yrif-y che sostituita nella precedente fornisce la rappresentazione nello spazio di stato del sistema ad anello chiuso:
\left \{ \begin{array}{ll} \dot{x}=Ax+B(y_{rif}-Cx)=(A-BC)x+By_{rif}\\y=Cx \end{array} \right.
e pertanto la F(s) – funzione di trasferimento in catena diretta del sistema ad anello aperto – assume un’espressione del tipo:
F(s)=C(sI-A)^{-1}B
dove i coefficienti C, A e B identificano le matrici dei parametri del sistema ad anello aperto e I è la matrice identità. L’obiettivo che ci si pone è legare la proprietà stabilità dei due sistemi.
Ora è noto (Teoria dei Sistemi) che se le soluzioni di DF(s) – i poli del prodotto delle funzioni di trasferimento G(s)H(s) – sono tutti in LHP (Left-Half Plane, semipiano sinistro), quindi a parte reale negativa, il sistema ad anello aperto è stabile asintoticamente il che vuol dire che in assenza di segnali esterni il sistema converge asintoticamente verso l’equilibrio, verso uno stato di riposo. Viceversa se esiste qualche soluzione nell’RHP il sistema ad anello aperto è instabile.
Ma la stabilità o meno di un sistema ad anello aperto ha poca importanza in questo contesto poiché ciò che interessa è la stabilità di un sistema ad anello chiuso. È noto come la retroazione ha la capacità di stabilizzare – almeno entro certi limiti! – un sistema ad anello aperto instabile, per tale motivo l’attenzione non può che spostarsi verso la funzione al denominatore della f.d.t ad anello chiuso, ovvero:
1+G(s)H(s)=1+F(s)=1+\frac{N_F(s)}{D_F(s)}=\frac{D_F(s)+N_F(s)}{D_F(s)}\kern{1cm}(2)
per la quale occorre notare che:
- Il numeratore altro non è che il denominatore della funzione di trasferimento ad anello chiuso. Infatti è facile verificare che:
\frac{U(s)}{I(s)}=\frac{F(s)}{1+F(s)}=\frac{N_F(s)}{D_F(s)+N_F(s)} - Il denominatore è il polinomio caratteristico (ovvero il denominatore) della funzione di trasferimento ad anello aperto, ovvero della F(s)=G(s)H(s).
In altre parole è possibile riscrivere la (2), tenendo anche conto della rappresentazione nello spazio di stato richiamata poco sopra per sistemi ad 1 solo ingresso e 1 sola uscita:
1+F(s)=\frac{D_{chiuso}(s)}{D_{aperto}(s)}=\frac{det[(sI-(A-BC)]}{det(sI-A)}\kern{1cm}(3)
In definitiva numeratore e denominatore sono dei polinomi e in quanto tali possono essere fattorizzati in funzione delle loro soluzioni laddove, per la fisica realizzabilità, l’ordine del polinomio a numeratore deve essere di grado inferiore o al limite pari al grado del denominatore, viceversa si avrebbe un sistema improprio. La (2) può così riscriversi:
\frac{D_F(s)+N_F(s)}{D_F(s)}=\frac{(s-\beta_1)(s-\beta_2)\dots (s-\beta_{m-1})(s-\beta_m)}{(s-\alpha_1)(s-\alpha_1)\dots (s-\alpha_{n-1})(s-\alpha_n)}\text{ con} \space m\le n\kern{1cm}(4)
Nyquist intuì un procedimento grafico subordinato alla costruzione grafica sul piano complesso della funzione di risposta armonica F(ιω). A seguire, più in là nella trattazione, ne viene riportata la “giustificazione” (leggasi dimostrazione) analitica che fa uso delle funzioni complesse. Subito, invece, il concetto alla base della suddetta costruzione da un punto di vista pratico/grafico.
Dato un qualunque punto p=σ+ιω appartenente al piano complesso S, e data la funzione a denominatore della f.d.t ad anello chiuso, è possibile scrivere, sostituendo in essa le coordinate del punto p:
1+G(s)H(s)=1+G(\sigma+\imath\omega)H(\sigma+\imath\omega)
il cui risultato, un numero complesso del tipo w=u+ιv, può essere riportato in un altro piano complesso battezzato come piano W. Ad esempio:
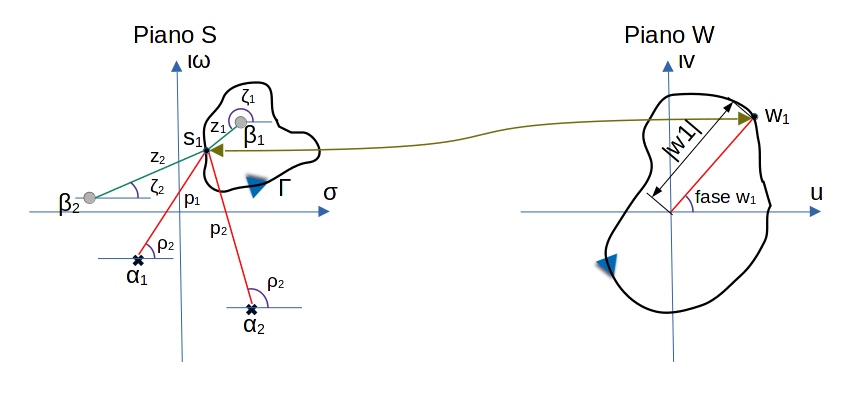
Nella figura in alto sono rappresentati 2 poli con la x e due zeri con il tondino pieno in grigio chiaro. Al dato punto s1 appartenente al percorso chiuso Γ nel piano complesso S corrisponde un ben preciso punto w1 nel piano W. Come lo si ricava? La (4) per 2 poli e 2 zeri può essere semplicemente riscritta come:
1+G(s)H(s)=\frac{(s-\beta_1)(s-\beta_2)}{(s-\alpha_1)(s-\alpha_2)}
Per un generico contorno Γ nel piano S, come quello riportato nella figura in alto, è evidente come ad ogni punto del contorno Γ sostituito nella precedente sia possibile riportare un corrispondente punto nel piano W. Allora tutti i punti del contorno Γ potranno essere mappati nel piano W con opportuno valore del modulo e della fase, laddove:
- La fase viene calcolata dalla (4), o sua particolarizzazione come nel caso di due poli e due zeri, come differenza della fase del numeratore meno la fase del denominatore;
- Il modulo viene calcolato dalla (4), o sua particolarizzazione come nel caso di due poli e due zeri, come rapporto del modulo del numeratore diviso il modulo del denominatore. Graficamente il modulo è rappresentato dalla lunghezza del segmento congiungente il punto s generico appartenente al contorno Γ con il polo/zero preso in esame.
Per l’esempio in questione risulta, considerando la simbologia adottata nella figura in alto:
1+G(s)H(s)=\frac{(s-\beta_1)(s-\beta_2)}{(s-\alpha_1)(s-\alpha_2)}=\frac{z_1 z_2}{p_1 p_2}e^{\imath(\zeta_1+\zeta_2-\rho_1-\rho_2)}
che fornisce modulo e fase del punto w1 nel piano W:
\left \{ \begin{array}{ll} |w_1|=\frac{z_1 z_2}{p_1 p_2} \\ \phase{w_1}=\phase{(\zeta_1+\zeta_2)-(\rho_1+\rho_2)} \end{array} \right.
Reiterando la procedura per ogni singolo punto appartenente al contorno chiuso Γ del piano S risulteranno un analogo numero di punti nel piano W che danno luogo ad un contorno chiuso (curva) nel piano W.
Si punti ora l’attenzione sulla fase di ogni singolo punto, poli o zeri che siano. È facile rendersi conto di come al variare di s sul contorno Γ lo zero β1 contribuirà con una fase pari a 2π. I punti all’esterno del contorno invece contribuiranno per una fase totale pari a 0. Infatti prendendo, ad esempio, lo zero β2 si può facilmente osservare come al variare di s sul contorno Γ la variazione totale della fase è pari a 0. Medesime considerazioni per i due poli α1 e α2 che contribuiranno con una fase pari a 0. Questo significa che l’unico zero contenuto nel contorno Γ genererà la curva nel piano W con una sola rotazione positiva (variazione di fase dello zero pari a 2π), quindi con medesimo verso di rotazione, attorno all’origine
Se vi fossero 2 zeri all’interno del contorno risulterebbe evidente come la fase varierebbe di un valore pari alla somma dei due contributi, ovvero 4π, in pratica 2 giri nel piano W. È altresì evidente come la presenza di un polo all’interno del contorno Γ darebbe luogo ad una variazione di fase pari a -2π, ovvero -4π in presenza di due poli e così via discorrendo. E in presenza di zeri e poli all’interno del contorno Γ? Semplice, la fase varierà di 2π un numero di volte pari a quanti sono gli zeri, considerando anche la loro molteplicità, sottratta di 2π del numero di poli e relativa molteplicità.
Nell’immagine si percorre il contorno Γ in senso antiorario quindi anche la curva sul piano W è percorsa nello stesso senso. Va da se che nulla cambierebbe se il contorno Γ venisse percorso in senso orario; in questo caso anche la curva nel piano W sarebbe in senso orario e la differenza di fase zero-poli continuerebbe a valere.
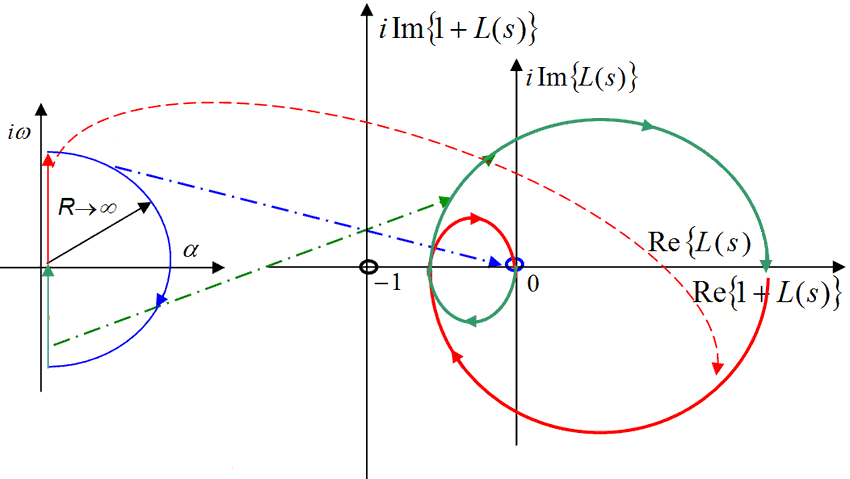
Ritornando alla funzione 1+G(s)H(s)=1+F(s), l’obiettivo principale è la valutazione della presenza o meno di poli a parte reale positiva (quindi che giacciono nell’RHP, asse immaginario compreso). Per ottenere questo risultato occorre identificare i punti s appartenenti al piano S in un contorno particolare che va sotto il nome di contorno (o percorso) di Nyquist comprendente l’intero semipiano reale positivo nel quale è compreso l’asse immaginario.
Il contorno Γ in color magenta riportato nell’immagine permette di mappare l’intero piano S nel semipiano reale positivo. Ogni punto nel piano S appartenente a questo particolare contorno, attraverso la 1+G(s)H(s) avrà il suo punto corrispondente nel piano W e l’insieme dei punti identificheranno in esso un contorno (curva chiusa); questa curva chiusa è detta diagramma di Nyquist.
Nella mappatura nel piano W l’interesse si sposta sul numero di giri del diagramma di Nyquist attorno all’origine (ovvero attorno al punto -1+j0), con una analisi a carattere qualitativo più che quantitativo.
In sostanza ponendo s=ιω si fa variare dapprima ω da 0+ a +∞ lungo l’asse immaginario. Va da se che per “spazzare” l’intero semipiano reale positivo corrispondente alla variazione del punto s=Reιθ sulla semicirconferenza di raggio tendente ad infinito, la fase θ del punto dovrà variare da +90° (+π/2) a -90° (-π/2).
Riprendendo la formula (4), ipotizzando in essa che il sistema risulti essere strettamente proprio ovvero grado del numeratore minore del grado del denominatore (m<n), sostituendo s=Reιθ e per R→∞ l’intera semicirconferenza all’infinito nel piano S è mappata nel piano W nell’origine. Se invece nella (1) risulta m=n – sistema proprio – l’intera semicirconferenza all’infinito verrà mappata nel piano W con un valore pari ad una costante sull’asse reale.
A questo punto il percorso riprende da ω=-∞ per terminare in ω=0–. Da osservare come la mappatura del percorso per ω variabile da -∞ a 0– risulta essere una immagine specchiata rispetto all’asse reale del grafico ottenuto con la pulsazione ω variabile da 0+ a +∞. Questa osservazione comporta che l’unica parte effettivamente da disegnare è solo quella relativa alle variazioni positive della pulsazione ω.
Per quanto detto in precedenza, se nel contorno Γ sono presenti P poli e Z zeri a parte reale positiva essi determineranno il numero di giri N (valore algebrico, può essere anche negativo) attorno all’origine in senso orario della funzione 1+G(s)H(s) nel piano W ovvero il numero di rotazioni orarie attorno all’origine del diagramma di Nyquist per ω che va da -∞ a +∞. Pertanto, tenendo conto della (3), il numero di giri sarà pari a “Soluzioni ℜ>0 Dchiuso(s)” sottratto a “Soluzioni ℜ>0 Daperto(s)“, in formule:
\overset{\curvearrowright}{N}=\Zeta_{chiuso}-\Zeta_{aperto}\kern{1cm}(5)
che identifica il noto criterio di Nyquist utilizzato per valutare la stabilità dei sistemi: la freccia sopra la N ricorda di considerare rotazioni in senso orario.
NOTA: In luogo dell’origine e della funzione 1+G(s)H(s)=1+F(s)=0 si può considerare G(s)H(s)=F(s)=-1 e prendere in considerazioni non più le rotazioni attorno all’origine della funzione 1+G(s)H(s)=1+F(s) ma le rotazioni intorno al punto -1+j0 della funzione G(s)H(s)=F(s). In sostanza la funzione 1+F(ιω), il suo grafico, è il grafico della funzione F(ιω) prendendo come origine il punto -1+j0.
In definitiva nell’applicazione del criterio di Nyquist occorre sempre ricordare che:
- N è il numero di giri in senso orario del diagramma di Nyquist attorno al punto -1+j0;
- Ζchiuso indica le radici a parte reale positiva del sistema ad anello chiuso – ovvero i poli della f.d.t. ad anello chiuso, quindi gli zeri della funzione 1+F(s) – presenti all’interno del percorso di Nyquist;
- Ζaperto indica le radici a parte reale positiva del sistema ad anello aperto – ovvero i poli della f.d.t ad anello aperto – presenti all’interno del percorso di Nyquist.
Le informazioni nella (5), ovvero i dati noti, sono relativi al sistema ad anello aperto; il numero di rotazioni N attorno all’origine della funzione 1+F(s), ovvero le rotazioni attorno al punto -1+j0 della funzione F(s) per ω che va da -∞ a +∞ e il numero di radici a parte reale positiva del polinomio caratteristico del sistema ad anello aperto Ζaperto. A partire da questi dati l’applicazione della (5) fornisce la risposta consistente nel numero di radici a parte reale maggiore di 0 presenti nel polinomio caratteristico del sistema ad anello chiuso, quello che è stato chiamato Ζchiuso. In tale scenario è evidente come si voglia che tale numero sia pari a 0, ovvero non esistano radici a parte reale positiva nel sistema ad anello chiuso.
Un’osservazione da fare per casi particolari. Riprendendo l’ultima immagine e la (3):
1+F(s)=\frac{D_{chiuso}(s)}{D_{aperto}(s)}
non sono da escludere la presenza di radici sull’asse immaginario. Ciò può accadere per il polinomio al numeratore, per il polinomio a denominatore oppure per entrambi. In più, non è noto a priori se il polinomio caratteristico ad anello chiuso presenti o meno radici sull’asse immaginario perché è una delle cose che ci si appresta a valutare, è l’effettiva incognita nello studio della stabilità quello di sapere dove sono collocati i poli del sistema ad anello chiuso. Ciò che potrebbe essere noto è la presenza di radici sull’asse immaginario del polinomio caratteristico ad anello aperto, la parte nota del problema dal quale si parte. Si distinguono così i casi:
- Si ipotizza che Dchiuso(s) presenti una radice immaginaria e che invece Daperto(s) non ne abbia. Questo vuol dire che per un certo valore immaginario puro s=ιω0 il numeratore si annulla il che significa 1+F(ιω0)=0 ovvero F(ιω0)=-1 quindi il diagramma di Nyquist passa per il punto -1 quando ω=ω0. Sotto questa ipotesi è evidente come il polinomio caratteristico ad anello chiuso ha una radice sull’asse immaginario e pertanto il sistema ad anello chiuso non può più essere stabile asintoticamente potendo avere al più una stabilità semplice.
- Situazione complementare, Daperto(s) presenta radici immaginarie e Dchiuso(s) non ne ha. Questo vuol dire che sicuramente il sistema ad anello aperto non è stabile asintoticamente, ma questo non interessa poiché il punto del discorso è avere un sistema ad anello chiuso stabile asintoticamente. Sarà proprio la chiusura dell’anello a poter eventualmente riuscire a stabilizzare il sistema. Dal punto di vista grafico questa situazione vede la F(ιω) tendere all’infinito per ω→ω0.
- Entrambi i polinomi, ad anello chiuso e ad anello aperto, possono presentare una radice sull’asse immaginario. Se non sono coincidenti si rientra nei precedenti punti se invece le radici sono coincidenti ecco che i due fattori a numeratore e denominatore possono semplificarsi e quindi la funzione 1+F(s) presenta una regolarità nel punto in questione, non va all’infinito. Ma questo non viene in nostro aiuto perché implicitamente vuol dire che il sistema ad anello chiuso presenta una radice sull’asse immaginario e pertanto non potrà mai essere stabile asintoticamente.
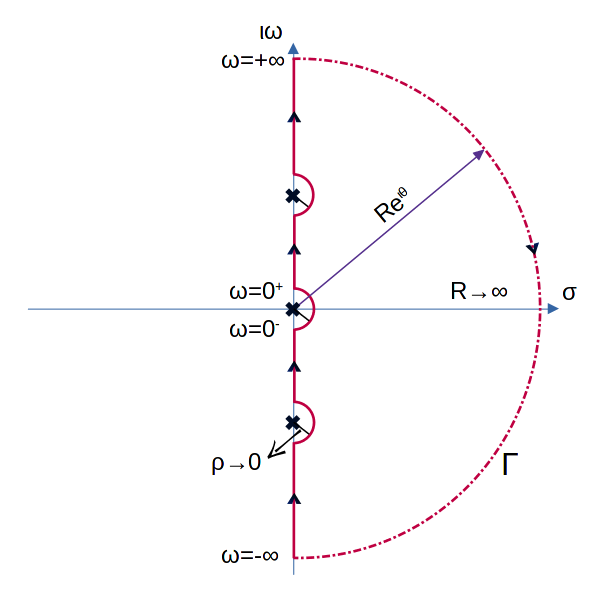
Quando si hanno radici sull’asse immaginario dobbiamo aspettarci una modifica per il percorso di Nyquist in base alle considerazioni che seguono. Ciò che crea problemi non sono gli zeri del polinomio ad anello chiuso per i quali la funzione va a zero, bensì gli zeri del polinomio ad anello aperto che mandano all’infinito il valore della funzione 1+F(s). In questo caso si può ipotizzare che le radici siano leggermente a sinistra dell’asse immaginario ovvero a parte reale “leggermente” negativa e quindi le si possono collocare tra le radici “buone”; il percorso sul contorno di Nyquist non viene “disturbato” ma comporta che il diagramma di Nyquist si modifica leggermente poiché non va più all’infinito ma rimane finito (seppure di valore molto elevato) e si completa con tante mezze rotazioni in senso orario quant’è la molteplicità del polo sull’asse immaginario (ovvero dello zero del polinomio ad anello aperto).
L’alternativa vede lasciare le radici sull’asse immaginario contornandole con una semicirconferenza di raggio ρ→0 esattamente come riportato nell’immagine in alto nella quale vengono rappresentati tre poli; uno nell’origine e l’altra coppia di poli complessi e coniugati. Poiché ρ→0 allora la funzione F(s), nell’intorno della singolarità ιω0 sull’asse immaginario, è rappresentabile come:
F(s)=\frac{1}{(s-\imath\omega_0)^n}[a_0+H(s)]
laddove a0≠0 e H(s) è una funzione analitica uguale a 0 per s=ιω0. La variazione di fase quando si percorre la suddetta semicirconferenza da ιω0– a ιω0+ in senso antiorario da luogo ad una F(s) che varia da F(ιω0–) a F(ιω0+) percorrendo una semicirconferenza di raggio infinito in senso orario. Questa affermazione è evidente se si calcola la variazione di fase in presenza di una radice immaginaria a denominatore. Il numero di semicirconferenze percorse in senso orario saranno tante quant’è la molteplicità del polo. Quindi se il polo sull’asse immaginario ha molteplicità 2 verranno percorse 2 semicirconferenze in senso orario (ovvero un giro completo), se molteplicità 3 verranno descritte 3 semicirconferenze e così via a seguire. In formule:
s=\lim_{\rho\to 0}(\imath\omega_0+\rho e^{\imath\alpha})\text{, } \alpha\isin\left(-\frac{\pi}{2},\frac{\pi}{2}\right) \Rightarrow F(s)\rightarrow\infin
Esempi
Analogamente ai diagrammi di Bode, molto spesso è utile saper tracciare il diagramma di Nyquist in maniera veloce e qualitativa e deducendolo, ad esempio, dagli stessi diagrammi di Bode oppure dal diagramma poli-zeri della F(s) (eventualmente utilizzando i diagrammi di Bode come verifica). Nel seguito per la visualizzazione degli esempi verrà utilizzato il noto programma Scilab.
Esempio numero 1
Sia data la funzione di trasferimento ad anello aperto:
F(s)=\frac{k}{(s+1)(s+3)}
con guadagno a numeratore variabile k=1, 2, 3. La funzione presenta un polo doppio all’infinito quindi trattasi di sistema strettamente proprio.
È subito visto che non vi sono poli a parte reale positiva e nemmeno sull’asse immaginario pertanto si è in presenza di un sistema ad anello aperto asintoticamente stabile. Percorrendo il contorno di Nyquist per ω da 0+ a +∞ non si incontrano poli sull’asse immaginario e non vi sono poli nell’RHP e il modulo |F(ιω)| decresce a 0 all’aumentare della frequenza (pulsazione).
s=%s;
num1=1;
num2=2;
num3=3;
den=(s+1)*(s+3);
G1=syslin('c',num1,den)
G2=syslin('c',num2,den)
G3=syslin('c',num3,den)
bode([G1;G2;G3],0.001,1000,['G1';'G2';'G3'])
nyquist([G3;G2;G1],["G3","G2","G1"])
È possibile valutare l’andamento dei diagrammi di Bode e del diagramma di Nyquist utilizzando le righe sopra riportate all’interno della console di Scilab (pannello centrale). Il risultato è mostrato nelle immagini in basso. È facile verificare come per ω=0 il modulo è pari a 1/3, 2/3 e 1 rispettivamente per k variabile da 1 a 3.
Va da se che per i diagrammi di Bode la fase non viene alterata con il variare del modulo del numeratore, ma l’aumento (diminuzione) del modulo si rileva sul diagramma dei moduli con una traslazione della curva verso l’alto (basso). Nel diagramma di Nyquist si ha un aumento della dimensione dello stesso, infatti all’aumentare del modulo il valore della funzione è maggiore a parità di frequenza.
Sulla stabilità non c’è molto da dire. Il vettore 1+F(jω), nel percorrere la curva al variare di ω, non fa alcun giro completo intorno al punto -1+j0. Prendendo in considerazione la (5) risulta che il numero di poli a parte reale positiva è zero, ne consegue Zaperto=0. Anche al crescere di k è visibile come N=0 (il punto -1+j0 è molto a sinistra rispetto all’immagine che vede l’ascissa “fermarsi” al valore -0,2) quindi il sistema ad anello chiuso sarà caratterizzato da un valore Zchiuso=N+Zaperto=0 con ovvia conseguenza che non avrà poli a parte reale positiva pertanto risulterà asintoticamente stabile indipendentemente dal valore di k.
Esempio numero 2
Sia data la funzione di trasferimento ad anello aperto:
F(s)=\frac{60}{(s+1)(s+2)(s+5)}
Si è in presenza di una funzione con triplo polo all’infinito e con poli tutti a parte reale negativa pertanto il sistema ad anello aperto è asintoticamente stabile. Al solito per tracciare il (o comprendere meglio l’andamento del) diagramma di Nyquist ci si può aiutare con i diagrammi di Bode che con Scilab è possibile tracciare utilizzando la console oppure Scinotes (l’embedded Scilab text editor dal menù Applicazioni) copiando le seguenti righe in un file di nome Esempio2.sce e mandandolo in esecuzione con il classico pulsante Play (Esegui):
w=logspace(-2,3,100000); s=%i*w num=poly([60 0],'s','c'); den=poly([1 1],'s','c')*poly([2 1],'s','c')*poly([5 1],'s','c'); F1jw=horner(num,%i*w)./horner(den,%i*w); modF1jw=20*log10(abs(F1jw)); faseF1jw=phasemag(F1jw); subplot(211),plot2d(w,modF1jw',logflag='ln'),xgrid subplot(212),plot2d(w,faseF1jw',logflag='ln'),xgrid
È evidente come la fase sia monotona decrescente passando da 0° a -270°, idem per il modulo il quale alle alte frequenze presenterà una pendenza di -60dB/dec.
Il modulo a frequenza 0 ha valore circa pari a 15,562dB ovvero, ricordando che dB=20 log10 X cioè che X=10dB/20, per ω=0 il modulo è 6. Come si può vedere dai datatips la fase è -180° per ω≅4,166rad/s e per questo valore il modulo vale circa -6,6dB; essendo un valore negativo in dB è evidente come il valore dell’ampiezza sia minore di 1, nello specifico circa 0,467. Questi valori permettono di intuire l’andamento del diagramma di Nyquist poiché per ω=0+ partirà dal valore 6, quando la fase è -180°, ovvero quando la curva del diagramma di Nyquist toccherà l’asse negativo delle ascisse, lo farà per un valore pari a circa 0,467 e via via che ω→∞ il modulo tende a 0 e la fase a -270°. La verifica dell’andamento del diagramma di Nyquist è possibile di nuovo utilizzando Scilab:
Dalla prima immagine si nota come per ω=0+ il grafico parta dal valore 6 (il modulo della f.d.t ad anello aperto quando la pulsazione è uguale a 0). Quando la fase è -180°, ovvero Y=0 nel grafico, dal datatips si nota come il valore risulti pari a 0,476 valore molto prossimo a quello valutato nel diagramma di Bode; la piccola discrepanza è dovuta al fatto che nel diagramma di Bode il datatips non era posto sopra i 4,166 rad/s ma a 4,159 rad/s. Da un punto di vista analitico è sufficiente valutare il valore di ω che annulla la parte immaginaria della funzione F(ιω). La seconda immagine, ingrandimento della prima, illustra come per ω→∞ il diagramma di Nyquist tenda ad una fase di -270°. Il diagramma è ottenuto riportando le righe che seguono nella console (pannello centrale) Scilab:
num=poly([60 0],'s','c') den=poly([1 1],'s','c')*poly([2 1],'s','c')*poly([5 1],'s','c') Fjw=num/den w=linspace(-350,350,30000); RF=horner(Fjw,%i*w); plot(real(RF),imag(RF)),xgrid
L’analisi della stabilità del sistema ad anello chiuso è immediata applicando la (5); la f.d.t ad anello aperto non ha poli a parte reale positiva, non vi sono rotazioni attorno al punto -1+j0, quindi Zchiuso=N+Zaperto=0 pertanto il sistema ad anello chiuso sarà asintoticamente stabile. Ma è sempre così? Proviamo ad aumentare il guadagno, ad esempio con l’obiettivo di ridurre l’errore e aumentare così la precisione, a passi del 50% fino ad arrivare, ad esempio, al 250% di quello iniziale utilizzando le righe:
colore=10;
w=linspace(-50,50,30000);
for k=1:0.5:2.5
num=poly([60*k 0],'s','c');
den=poly([1 1],'s','c')*poly([2 1],'s','c')*poly([5 1],'s','c');
Fjw=num/den
RF=horner(Fjw,%i*w);
plot(real(RF),imag(RF)),xgrid
colore_linea = gce();
colore_linea.children.foreground = colore;
if colore<=20 then
colore=colore+1;
else colore=10;
end
end
il risultato vede il seguente gruppo di andamenti:
Come è facile verificare, all’aumentare del guadagno cresce il grafico a parità di pulsazione e questo in alcuni casi, come quello in questione, gli permette di raggiungere e superare il punto -1+j0. Come visibile dai valori nei datatips nella sezione ingrandita, quando il guadagno assume il valore 120 il punto con fase -180° si trova ancora a destra di -1+j0 e assume valore -0.953. In termini di stabilità questa situazione è analoga alla precedente; il sistema ad anello chiuso è stabile …seppur con margini abbastanza risicati.
Ma cosa succede quando il guadagno assume valore 150 (ovvero k=2,5)? Come si può vedere il punto -1+j0 viene scavalcato e a -180° la funzione F(jω) assume il valore -1,191. In queste condizioni applicando la (5) e andando a contare il numero di rotazioni del vettore 1+F(jω) nel percorrere la curva al variare di ω, si scopre che esso compie 4 mezzi giri in senso orario ovvero 2 giri in senso orario. Siccome la funzione di trasferimento ad anello aperto non è cambiata allora risultano sempre 0 poli a parte reale positiva e quindi in definitiva Zchiuso=N+Zaperto=2+0=2 quindi il sistema ad anello chiuso, per il valore del guadagno indicato, si troverà 2 poli con parte reale positiva, giacenti nell’RHP, e in quanto tali, per quel valore del guadagno, il sistema ad anello chiuso risulterà essere instabile!
Esempio numero 3
Sia data la funzione di trasferimento ad anello aperto:
F(s)=\frac{k}{s(s+10)}La funzione di trasferimento ad anello aperto presenta un polo nell’origine e un polo a parte reale negativa. I diagrammi di Bode e Nyquist risultano, previo uso di Scilab con l’utilizzo di righe di codice simili a quelle riportate in Esempio 1:
È subito visto come il diagramma dei moduli ha il suo punto iniziale a -20dB/dec a causa del polo nell’origine per poi andare a -40dB/dec a causa dell’altro polo. La fase parte da -90° vista la presenza del polo nell’origine per poi andare a finire a -180° per ω→+∞ a causa dell’altro polo.
È evidente come nel diagramma di Nyquist manchi la chiusura all’infinito, in particolare le corrispondenze tra il percorso di Nyquist e il diagramma di Nyquist vengono riportate in basso per maggiore comprensione:
Che cosa si può dire sulla stabilità del sistema ad anello chiuso? Come è facile vedere nel diagramma di Nyquist, il punto -1+j0 non “entra mai in gioco” poiché per ogni valore di K i valori del diagrammi si trovano sotto l’asse delle ascisse per valori di ω positivi (sopra l’asse delle ascisse per valori di ω negativi). Questo implica che il numero di giri N=0. Ma il numero di poli a parte reale positiva del sistema ad anello aperto è pari a 0 pertanto dalla (5) è possibile scrivere Zchiuso=N+Zaperto=0+0=0, ovvero il sistema ad anello chiuso non ha poli a parte reale positiva (o sull’asse immaginario) pertanto è asintoticamente stabile e questo è vero per ogni valore di K.
Esempio numero 4
Funzione di tarsferimento ad anello aperto simile alla precedente, viene aggiunto un ulteriore polo nell’origine:
F(s)=\frac{k}{s^2(s+10)}I diagrammi di Bode, analogamente all’esempio precedente, sono immediati. Infatti il diagramma dei moduli parte con una pendenza di -40dB/dec per la presenza di un polo nell’origine con molteplicità 2, per continuare per valori della pulsazione ω→+∞ con -60dB/dec quando viene incontrato l’altro polo. Il diagramma delle fasi, ricordando che la periodicità è pari a π (180°), a causa del polo doppio nell’origine parte da 180° per poi “scendere” a 90° per il contributo dell’altro polo a parte reale negativa.
Da quanto riportato il diagramma di Nyquist partirà per ω=0+ da una fase di 180° con valore “infinito” per portarsi a 0 con fase 90° per ω→+∞. Si costruisce così lo speculare rispetto all’assa delle ascisse per ω variabile da -∞→0– quindi si “chiude” il diagramma da 0–→0+ con tanti mezzi giri quant’è la molteplicità del polo nell’origine. In definitiva, utilizzando in Scilab righe di codice simili a quelle riportate per Esempio 1, risulta:
È evidente come nel diagramma di Nyquist manchi la chiusura all’infinito. Per maggiore comprensione le corrispondenze tra il percorso di Nyquist e il diagramma di Nyquist vengono riportate di seguito:
 Come interpretare la stabilità? Un ingrandimento del diagramma di Nyquist (immagine a lato, un click per ingrandirla) in prossimità di -1+j0 evidenzia, e non poteva essere altrimenti, come il suddetto punto sia all’interno del diagramma di Nyquist. Allora percorrendo il diagramma da ω=-∞ fino a ω=+∞ si possono contare 4 semigiri (ovvero 2 giri) in senso orario – quindi positivi – attorno al punto -1+j0, il che comporta N=2. Ma il sistema ad anello aperto, la cui funzione di trasferimento è stata data all’inizio dell’esempio, non presenta poli a parte reale positiva pertanto dalla (5) si può scrivere Zchiuso=N+Zaperto=2+0=2 ovvero il sistema ad anello chiuso sarà caratterizzato da 2 poli a parte reale positiva e quindi risulterà instabile!
Come interpretare la stabilità? Un ingrandimento del diagramma di Nyquist (immagine a lato, un click per ingrandirla) in prossimità di -1+j0 evidenzia, e non poteva essere altrimenti, come il suddetto punto sia all’interno del diagramma di Nyquist. Allora percorrendo il diagramma da ω=-∞ fino a ω=+∞ si possono contare 4 semigiri (ovvero 2 giri) in senso orario – quindi positivi – attorno al punto -1+j0, il che comporta N=2. Ma il sistema ad anello aperto, la cui funzione di trasferimento è stata data all’inizio dell’esempio, non presenta poli a parte reale positiva pertanto dalla (5) si può scrivere Zchiuso=N+Zaperto=2+0=2 ovvero il sistema ad anello chiuso sarà caratterizzato da 2 poli a parte reale positiva e quindi risulterà instabile!
Esempio numero 5
[In preparazione]
Dimostrazione analitica
A fronte di una facile applicazione e immediata comprensione (si spera!) il “back-end” che sottende l’applicazione del diagramma prima e del criterio di Nyquist in un secondo momento non è proprio dei più semplici poiché necessità di un minimo di conoscenze di Analisi Matematica I, II e III (o Metodi Matematici).
Nel seguito verranno richiamati – e laddove necessario anche dimostrati – teoremi e definizioni che portano alla dimostrazione di quanto applicato nei paragrafi precedenti. Va da se che verrà preso in considerazione solo ciò che è di interesse per ottenere il risultato senza eventuali conseguenze di un teorema laddove non dovesse essere necessario alla dimostrazione della tesi, nello specifico nella “giustificazione” dell’applicazione pratica del diagramma e criterio di Nyquist.
Le funzioni di variabile complessa
Definizione: sia \Gamma\subset\Complex un aperto connesso del campo complesso (ovvero, semplificando, un insieme nel quale una curva chiusa in esso contenuta può essere ridotta e contratta a piacimento fino ad un punto senza determinarne per questo l’uscita dal suddetto insieme) e sia:
f(z):\Gamma\subset\Complex\rightarrow\Complex \mid\forall z\isin \Gamma \implies f(z)=w\isin\wp\subset\Complex
allora la f(z) è una funzione di variabile complessa avente Γ come dominio e ℘=f(Γ) sarà l’immagine, il codominio. Una funzione w=f(z) per la quale z=x+\imath y \isin\Complex risulterà una associazione f(z):\Complex\rightarrow\Complex ovvero una trasformazione da punti z del piano complesso Z a punti dello stesso piano complesso che chiamiamo W, un endomorfismo nel quale dominio e codominio coincidono, nello specifico, con il piano complesso.

In altre parole, considerando l’immagine in alto, poiché w=f(z)\isin\Gamma\subset\Complex allora anche la f(z) è un numero complesso che da un punto di vista di principio può essere riscritta come Re[f(z)]+ιIm[f(z)] e nelle quali entrambe – parte reale e immaginaria – dipendono da z la quale, a sua volta, dipende dalle due variabili reali x e y. Questa osservazione permette di esprimere la funzione complessa in una forma algebrica dipendente da due funzioni, una per la parte reale e una per la parte immaginaria, ovvero f(z)=u(x,y)+ιv(x,y). Quindi, riassumendo, la somma di due funzioni di variabile reale e dove la u(x,y)=ℜf(z) e la v(x,y)=ℑf(z) dipendono entrambe da x e da y ovvero sono funzioni definite in \Gamma\subset\Complex e a valori in ℜ campo reale.
Per lo scopo in essere il primo passo è estendere la definizione di derivabilità per funzioni complesse. Nel campo reale (Analisi I) la derivata di una funzione di una variabile, e.g. y=f(x), è definita come il limite del rapporto incrementale per l’incremento tendente a 0. È possibile riprendere la stessa definizione e dire che una funzione complessa di variabili reali è derivabile se esiste ed è finito il limite del rapporto incrementale per l’incremento che tende a 0, in formule:
\lim_{\Delta{z}\to 0} \frac{f(z_0+\Delta{z})-f(z_0)}{\Delta{z}}=f^{'}(z_0)\kern{1cm}(D1)
ma attenzione perché questa volta la definizione riguarda il piano e pertanto è possibile tendere al punto riportato, e.g. z→z0, da infinite direzioni, per tale motivo la definizione dovrà essere indipendente dalla direzione lungo la quale si tende a z0 se si vuole che la derivata esista. In buona sostanza il solo Δz in modulo non è sufficiente a descrivere il rapporto incrementale poiché può essere preso in diverse direzioni, le congiungenti z0 con z appartenente al piano complesso, e affinché il suddetto rapporto esista occorre che il valore sia uguale qualsiasi sia la direzione presa per il calcolo. Se il valore è differente allora la derivata non esiste anche se la funzione è continua così come riportato dal seguente teorema.
Teorema: Sia f(z):\Gamma\subset\Complex\rightarrow\Complex se f(z) è derivabile in z0∈Γ allora f(z) è anche continua in z0, Il contrario non è vero; una funzione f(z) può essere continua in z0 senza che sia derivabile nello stesso punto ovvero conducendo a risultati differenti a seconda della direzione in base alla quale Δz→0.
Dimostrazione: Poiché per ipotesi la f(z) è derivabile in z0 allora risulta, dalla definizione (D1):
\lim_{\Delta{z}\to 0} \frac{f(z_0+\Delta{z})-f(z_0)}{\Delta{z}}=f^{'}(z_0)
È evidente come il numeratore possa scriversi come:
f(z_0+\Delta z)-f(z_0)=\frac{f(z_0+\Delta z)-f(z_0)}{\Delta z}\Delta z
e il limite di Δz→0 della precedente fornisce, ricordando le proprietà dei limiti, nello specifico che il prodotto del limite è uguale al limite dei prodotti:
\lim_{\Delta{z}\to 0}f(z_0+\Delta z)-f(z_0)=\lim_{\Delta{z}\to 0}\frac{f(z_0+\Delta{z})-f(z_0)}{\Delta{z}}\times \lim_{\Delta{z}\to 0} \Delta z=f^{'}(z_0) \times 0
poiché per ipotesi la f‘(z0) esiste allora non potrà che essere:
\lim_{\Delta{z}\to 0}f(z_0+\Delta z)-f(z_0)=0 \space \text{ cioé } \space \lim_{\Delta{z}\to 0}f(z_0+\Delta z)=f(z_0)
ovvero che la funzione f(z) è continua in z0. Più in la nella trattazione verranno richiamati alcuni concetti di Analisi II riguardanti funzioni di più variabili come la continuità, le derivate parziali, le derivate direzionali e la differenziabilità.
Anche per le funzioni complesse valgono e sono dimostrabili tutte le regole di derivazioni note dall’analisi, e.g. la derivata della somma di due o più funzioni, la nota regola della derivata del prodotto e del rapporto di due funzioni così come la regola di derivazione delle funzioni composte.
Condizione di olomorfia e analiticità
Definizione 1: una regione Γ si dice semplicemente connessa quando una linea semplice e chiusa che giace in essa può ridursi ad un punto senza uscire mai da Γ. Ad esempio un “cerchio pieno” è una regione semplicemente connessa, una “ciambella” è una regione molteplicemente connessa.

Definizione 2: convenzionalmente la frontiera della regione Γ, che si indica con ∂Γ, è percorsa in senso o verso positivo se un osservatore, giacente su di essa e normale al piano di percorrenza, mentre la percorre trova alla sua sinistra la regione Γ. Ad esempio il verso è antiorario sul contorno della regione e orario per curve che delimitano regioni molteplicemente connesse (immagine in alto). Alcune volte il verso positivo viene indicato con +∂Γ ad indicare il verso di percorrenza convenzionale.
Una funzione f(z) definita in una regione del piano complesso e a valori nel piano complesso, f(z):\Gamma\subseteq\Complex\rightarrow\Complex, si definisce olomorfa in Γ se per ogni punto z in Γ esiste la derivata della funzione f‘(z) ovvero:
\forall z=(x,y)\isin\Gamma\rightarrow f(z)=f(x,y)=u(x,y)+\imath v(x,y)
se
\forall z_0\isin\Gamma\space\exist \text{ ed è finito }\lim_{z\to z_0} \frac{f(z)-f(z_0)}{z-z_0}\isin\Complex
allora la f(z) è olomorfa in tutto il piano complesso. È il caso di analizzare le condizioni necessarie e sufficienti affinché una funzione di variabili reali, interpretata come funzione di variabile complessa, sia olomorfa. In tale veste ci viene in aiuto il seguente fondamentale teorema.
Teorema: le seguenti affermazioni sono del tutto equivalenti:
- Se f(z) è olomorfa allora esiste la f‘(z) per ogni punto z nella intera regione di definizione Γ;
- Se è vera la condizione 1) allora la f(z) è derivabile infinite volte e f(z) è detta analitica;
- Se è vera la condizione 1) allora la f(z) soddisfa le relazioni di Cuachy-Riemann.
Per il punto 1) la condizione di olomorfia richiede “solo” l’esistenza della derivata prima della funzione f(z) nella regione di definizione. Ma la condizione 1) comporta “automaticamente” l’esistenza di infinite derivate della funzione f(z) – affermazione 2) – cosa non veritiera per le funzioni reali di variabili reali, e.g. f(x,y), per le quali (Analisi II) l’esistenza della derivata prima non comportava automaticamente l’esistenza della derivata seconda come avviene, invece, per le funzioni di variabile complessa. Pertanto se la f(z) ha derivata prima, “automaticamente” esiste la derivata di ogni ordine e quindi la funzione è analitica; l’analiticità è legata anche alla convergenza di raggio non nullo della serie di Taylor corrispondente. Appare ovvio allora come l’analiticità comporti l’olomorfia e, per quanto detto sull’esistenza della derivata prima e di ordine superiore, avere una funzione olomorfa implica avere una funzione analitica.
Formule (equazioni o condizioni) di Cauchy-Riemann
Condizione necessaria affinché la funzione w=f(z)=u(x,y)+\imath v(x,y):\Gamma\subseteq\Complex\rightarrow\Complex sia analitica nella regione Γ è che, nella stessa regione, le funzioni u(x,y) e v(x,y) soddisfino le equazioni di Cauchy-Riemann:
\frac{\partial{u}}{\partial{x}}=\frac{\partial{v}}{\partial{y}} \text{ ; } \frac{\partial{u}}{\partial{y}}=-\frac{\partial{v}}{\partial{x}}\kern{1cm}(D2)
Ovvero il limite del rapporto incrementale non deve dipendere dalla direzione ed esistendo la derivata prima la funzione è olomorfa ovvero analitica.
Non separando parte reale e immaginaria della funzione f(z) la precedente condizione può essere scritta come:
\frac{\partial{f(z)}}{\partial{x}}=\frac{1}{\imath}\frac{\partial{f(z)}}{\partial{y}}
Se inoltre le suddette derivate parziali sono continue in Γ le (D2) definiscono anche le condizioni sufficienti di analiticità della funzione f(z) in Γ.
La condizione è necessaria
Per dimostrare la condizione necessaria occorre dimostrare che il limite del rapporto incrementale esiste e che non dipende dal modo (direzione) in cui Δz, ovvero Δx e Δy, tende a zero. Riprendendo la definizione di rapporto incrementale, ricordando che f(z)=u(x,y)+ιv(x,y) con z0=x0+ιy0 e Δz=Δx+ιΔy, sostituendo tali valori nella (D1) risulta:
\lim_{\substack{\Delta{x}\to 0\\\Delta{y}\to 0}}\frac{[u(x_0+\Delta{x},y_o+\Delta{y})+\imath v(x_0+\Delta{x},y_o+\Delta{y})-[u(x_0,y_0)+\imath v(x_0,y_0)]}{\Delta{x}+\imath\Delta{y}}\kern{1cm}(D3)
Ora se si fa tendere a zero il rapporto incrementale spostandosi lungo una direzione parallela all’asse delle ascisse (asse reale) implica che la coordinata y non varia ovvero Δy=0 mentre, per quanto detto, Δx→0. Allora la (D3) è possibile riscriverla come:
\lim_{\Delta{x}\to 0}\frac{[u(x_0+\Delta{x},y_o)+\imath v(x_0+\Delta{x},y_o)-[u(x_0,y_0)+\imath v(x_0,y_0)]}{\Delta{x}}
dalla quale. raccogliendo i termini reali e immaginari al fine di renderli identificabili ad un rapporto incrementale, è possibile scrivere:
\left[ \lim_{\Delta{x}\to 0}\frac{[u(x_0+\Delta{x},y_o)-u(x_0,y_0)}{\Delta{x}}\right]+\imath\left[\lim_{\Delta{x}\to 0}\frac{v(x_0+\Delta{x},y_o)-v(x_0,y_0)}{\Delta{x}}\right]
Ora, come noto da Analisi II (richiami in basso), per Δx→0 il limite tra parentesi quadre a sinistra altro non è che la definizione della derivata parziale di u rispetto a x e il termine entro parentesi quadre a destra è invece la definizione della derivata parziale di v rispetto a x pertanto si può scrivere:
\frac{\partial{u}}{\partial{x}}\bigg|_{(x_0,y_0)}+\imath \frac{\partial{v}}{\partial{x}}\bigg|_{(x_0,y_0)}=f^{'}(z_0)\kern{1cm}(D4)
Affinché la definizione risulti essere consistente, il valore che si ottiene facendo tendere a zero il rapporto incrementale spostandosi lungo una direzione parallela, questa volta, all’asse delle ordinate (asse immaginario), ovvero quando la coordinata x non varia e quindi Δx=0 e con Δy→0, deve risultare uguale al risultato precedente. In sostanza, con medesima procedura:
\left[ \lim_{\Delta{y}\to 0}\frac{[u(x_0,y_o+\Delta{y})-u(x_0,y_0)}{\imath\Delta{y}}\right]+\cancel{\imath}\left[\lim_{\Delta{y}\to 0}\frac{v(x_0,y_o+\Delta{y})-v(x_0,y_0)}{\cancel{\imath}\Delta{y}}\right]
e con analoghe considerazioni si può scrivere, ricordando che 1/ι è uguale a -ι:
\frac{1}{\imath}\frac{\partial{u}}{\partial{y}}\bigg|_{(x_0,y_0)}+\frac{\partial{v}}{\partial{y}}\bigg|_{(x_0,y_0)}=-\imath\frac{\partial{u}}{\partial{y}}\bigg|_{(x_0,y_0)}+\frac{\partial{v}}{\partial{y}}\bigg|_{(x_0,y_0)}=f^{'}(z_0)\kern{1cm}(D5)
Ora affinché la funzione f(z) risulti analitica il risultato della (D4) deve essere uguale a quanto ottenuto nella (D5) poiché solo così si ha che f‘(z0) esiste ed è indipendente dal cammino percorso per andare da z a z0. Ma eguagliare la (D4) con (D5), poiché trattasi di due numeri complessi, implica eguagliare parte reale con parte reale e parte immaginaria con parte immaginaria, ovvero:
\frac{\partial{u}}{\partial{x}}+\imath\frac{\partial{v}}{\partial{x}}=\frac{\partial{v}}{\partial{y}}-\imath\frac{\partial{u}}{\partial{y}}
e restano così dimostrate le condizioni (D2).
NOTA: In quanto condizione necessaria va da se che se le relazioni di Cauchy-Riemann non sono verificate allora la funzione f(z) non è derivabile in senso complesso e pertanto non è analitica.
Richiami Analisi II
Prima di procedere con la dimostrazione della condizione sufficiente occorrono alcuni concetti di Analisi II; al solito si prenderanno in considerazione solo quelli di interesse in questo scenario cercando di arrivare in “maniera verticale” all’obiettivo prescindendo da concetti e teoremi “laterali” (altrimenti non se ne esce più 🙂 ).
Definizione 1: la definizione di continuità per funzioni di più variabili può essere vista in due modi differenti; in termini di intorni risulta:
\text{Sia } f:A\subset\R^n\to\R \text{ essa è continua in } x^0=(x^{0}_1,x^{0}_2,\dots,x^{0}_n)^T\\\Updownarrow\\\forall \text{ V intorno di } f(x^0) \exist \text { U intorno di } x^0\mid\forall x\isin U\cap A\implies f(x)\isin\text{ V}
Ad esempio nel caso più semplice e intuitivo di una funzione a due variabili, ovvero in \R^2:
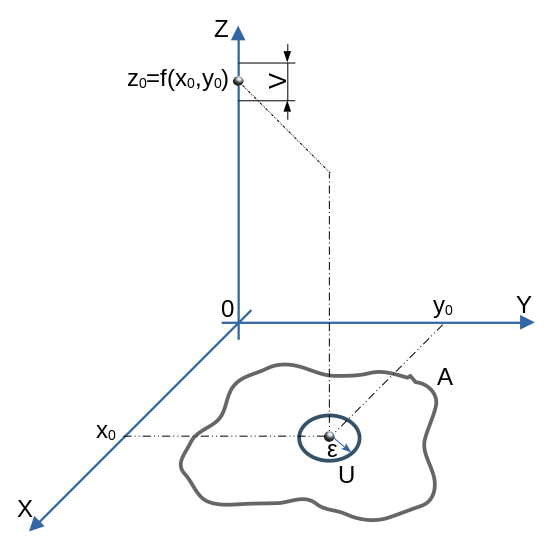
Definizione 2: una seconda definizione potrebbe ricordare un qualcosa di simile alla definizione per funzioni ad una variabile, cioè:
\text{Sia } f:A\subset\R^n\to\R \text{ e } x^0\isin\text{A allora f è continua in } x^0\\\Updownarrow\\\forall\epsilon\gt0\exist\delta_{\epsilon}\gt0\mid\forall x\isin\text{A se }|x-x^0|\lt\delta_{\epsilon}\implies|f(x)-f(x^0)|\lt\epsilon
laddove si ricorda che:
|x-x^0|=\sqrt{\sum_{i=1}^{n}(x_i-x^{0}_i)^2}
Ora per una funzione a più variabili (2 in questo contesto) è possibile definire le derivate parziali e le derivate direzionali. Infatti nel caso di più variabili (minimo 2) ci si potrebbe chiedere rispetto a cosa o a chi andare a derivare.
\text{Sia } f:A\subset\R^2\to\R \text{ allora } \forall x^0\isin\text{A e }\forall\epsilon\gt0\mid\text{U}\subset\text{A}
ovvero per ogni ε>0 tutti i punti di U sono contenuti in A (con riferimento alla immagine precedente). Per definizione di rapporto incrementale – e.g. la (D1) – fare la derivata parziale rispetto a x implica:
\frac{\partial{f(x_0,y_0)}}{\partial{x}}=\lim_{x\to x_0}\frac{f(x,y_0)-f(x_0,y_0)}{x-x_0}
altrimenti detto si mantiene fissa la y=y0 e si fa variare la x. Stessa considerazione se si vuole valutare la derivata parziale rispetto ad y:
\frac{\partial{f(x_0,y_0)}}{\partial{y}}=\lim_{y\to y_0}\frac{f(x_0,y)-f(x_0,y)}{y-y_0}
Più in generale la definizione di derivata parziale per funzioni di più variabili (maggiori di 2) si può scrivere:
\frac{\partial{f(x^{0}_1,x^{0}_2,\dots,x^{0}_k,\dots,x^{0}_n)}}{\partial{x_k}}=\lim_{x_k\to x^{0}_k}\frac{f(x^{0}_1,x^{0}_2,\dots,x_k,\dots,x^{0}_n)-f(x^{0}_1,x^{0}_2,\dots,x^{0}_k,\dots,x^{0}_n)}{x_k-x^{0}_k}
Ora sia ξ=(ξ1,ξ2,…ξn)T un vettore di versori (modulo unitario) della base \R^n. Allora considerata la retta di equazione x(t)=x0 +ξ*t, passante per x0 e avente direzione ξ, si definisce derivata direzionale della funzione f lungo ξ nel punto x0 il limite del rapporto incrementale:
\frac{\partial{f(x^{0}_1,x^{0}_2,\dots,x^{0}_k,\dots,x^{0}_n)}}{\partial{\xi}}=\lim_{t\to 0}\frac{f(x^0+\xi\times t)-f(x^0)}{t}
Per funzioni a più variabili l’esistenza di tutte le derivate direzionali non implica automaticamente la continuità della funzione. Per funzioni a più variabili si rende necessaria una condizione più forte affinché la funzione risulti continui e ciò perché tanto le derivate parziali quanto le derivate direzionali forniscono condizioni meno stringenti se paragonate alla derivata di funzioni ad una variabile. Altrimenti detto, a differenza delle funzioni a una variabile reale del tipo y=f(x) per le quali l’esistenza della derivata (ovvero l’essere derivabile) ne comporta la sua continuità, per funzioni a più variabili questo non è più vero pertanto occorre la condizione più stringente indotta dalla differenziabilità della funzione. La definizione di differenziale per funzioni a più variabili vede:
\text{Sia } f:A\subset\R^n\to\R \text{ si dice differenziabile in } x^0=(x^{0}_1,x^{0}_2,\dots,x^{0}_n)^T\isin\text{A}\\\Updownarrow\\\exist\text{ una applicazione lineare }L:A\subset\R^n\to\R
tale che risulti:
f(x)=f(x^0)+L(x-x^0)+\epsilon(x)|x-x^0|
con ε(x)→0 quando x→x0. Il teorema che segue definisce delle condizioni sufficienti per la continuità di funzioni a più variabili.
Teorema 1: Se la funzione a più variabili f(x1,x2,…,xk,…,xn) è differenziabile in x^0=(x^{0}_1,x^{0}_2,\dots,x_k,\dots,x^{0}_n)^T allora è anche continua in x0.
Dimostrazione: Dalla definizione di differenziale dovrà esistere una applicazione lineare L:A\subset\R^n\to\R riscrivibile esplicitamente come:
L(x-x^0)=L_1(x_1-x^{0}_1)+L_2(x_2-x^{0}_2)+\dots+L_n(x_n-x^{0}_n)
con L1,L2,…,Ln numeri reali. Infatti definendo ei i versori della base canonica è possibile scrivere:
x-x^0=(x_1-x^{0}_1)e_1+(x_2-x^{0}_2)e_2+\dots+(x_n-x^{0}_n)e_n
ed essendo L una applicazione lineare applicata a x-x0 allora per definizione stessa di applicazione lineare (Geometria) è possibile riscrivere:
L(x-x^0)=(x_1-x^{0}_1)L(e_1)+(x_2-x^{0}_2)L(e_2)+\dots+(x_n-x^{0}_n)L(e_n)=\\[1.2em]=L_1(x_1-x^{0}_1)+L_2(x_2-x^{0}_2)+\dots+L_n(x_n-x^{0}_n)
laddove Ln è il valore che la forma lineare assume sul versore en della base canonica. A questo punto è abbastanza immediato dimostrare il teorema nel momento in cui si riesce a dimostrare che:
\lim_{x\to x^0}f(x)=f(x^0)
Infatti se per ipotesi la funzione è differenziabile in x0 allora si può scrivere, dalla definizione di differenziale:
f(x)=f(x^0)+L(x-x^0)+\epsilon(x)(x-x^0)=\\[1.2em]=f(x^0)+L_1(x_1-x^{0}_1)+L_2(x_2-x^{0}_2)+\dots+L_n(x_n-x^{0}_n)+\epsilon(x)|x-x^0|
ma per x→x0 tutti i termini del secondo membro a partire dal secondo addendo vanno a 0 il che significa aver dimostrato che:
\lim_{x\to x^0}f(x)=f(x^0)\\[1.2em]c.v.d.
Teorema 2: Se f(x1,x2,…,xk,…,xn) è differenziabile in x0=(x01,x02,…,x0k,…,x0n)T allora la funzione f(x1,x2,…,xk,…,xn) ha derivate in ogni direzione nel punto x0 e, in particolare, esistono tutte le derivate parziali.
Dimostrazione: sia v un vettore di \R^n\mid\|v\|=1, ovvero un vettore di versori in \R^n e sia x=x0 +v*t l’equazione della retta passante per x0 e di direzione v. Poiché |v|=1 allora è immediato il risultato |x-x0|=|v*t|=|v|*|t|=|t|, ricordando anche che il valore assoluto di un prodotto è uguale al prodotto dei valori assoluti. Va da se allora che, per quanto riportato in precedenza:
\frac{f(x^0+v\times t)-f(x^0)}{t}
per definizione altro non è che la derivata della f(x1,x2,…,xk,…,xn) calcolata in x0=(x01,x02,…,x0k,…,x0n)T e direzione v. Ma per ipotesi la funzione è differenziabile e allora si può riscrivere, per definizione di differenziale, semplificando e sostituendo in un secondo momento il valore x=x0 +v*t e ricordando anche la definizione di applicazione lineare:
\frac{f(x^0+v\times t)-f(x^0)}{t}=\frac{\cancel{f(x^0)}+L(x-x^0)+\epsilon(x)|x-x^0|-\cancel{f(x^0)}}{t}=\\[1.2em]=\frac{+L(\cancel{x^0}+v\times t-\cancel{x^0})+\epsilon(x^0+v\times t)|\cancel{x^0}+v\times t-\cancel{x^0}|}{t}=\frac{L(vt)+\epsilon(x^0+v\times t)|vt|}{t}=\\[1.2em]=\frac{tL(v)+\epsilon(x^0+v\times t)|t|}{t}=L(v)+\epsilon(x^0+v\times t)\frac{|t|}{t}
Ora per x→x0, cioè per t→0, l’infinitesimo di ordine superiore ε tende a 0 per definizione mentre il rapporto in t ∀t≠0 e t→0 si mantiene limitato (valore ±1), pertanto il prodotto con ε tende a 0. In definitiva si è dimostrato che esiste ed è finito il limite:
\lim_{t \to 0}\frac{f(x^0+v\times t)-f(x^0)}{t}=L(v)=L_1(v_1)+L_2(v_2)+\dots+L_n(v_n)\triangleq\frac{\partial{f(x^0)}}{\partial{v}}
che, per definizione di rapporto incrementale, altro non è che la derivata parziale in direzione v calcolata nel punto x0. In particolare quando la direzione coincide con il versore k-esimo ek di \R^n è possibile scrivere:
\frac{\partial{f(x^0)}}{\partial{e_k}}=L(e_k)=L_1\times 0+L_2\times 0+\dots+L_k\times 1+\dots+L_n\times 0=L_k=\frac{\partial{f(x^0)}}{\partial{x_k}}
che identifica l’importante risultato della derivata parziale rispetto a xk calcolata in x0. Altrimenti detto è stata calcolata la derivata direzionale lungo la direzione del versore ek ovvero data la retta di equazione x=x0 +t*ek passante per x0 e direzione ek per la quale si può scrivere (fissata la direzione ek):
\left \{ \begin{array}{ll} x_1=x^{0}_1+t\times 0\\x_2=x^{0}_2+t\times 0\\\vdots \\x_k=x^{0}_k+t\times 1\\\vdots \\x_n=x^{0}_n+t\times 0 \end{array} \right.
pertanto:
\frac{\partial{f(x^0)}}{\partial{e_k}}=\lim_{t \to 0}\frac{f(x^{0}_1,\dots,x^{0}_k+t,\dots,x^{0}_n)-f(x^0)}{t}
ora, poiché xk=x0k+t allora t=xk-x0k e il limite precedente si può riscrivere come:
\lim_{t \to 0}\frac{f(x^{0}_1,\dots,x^{0}_k+t,\dots,x^{0}_n)-f(x^0)}{t}=\lim_{x_k \to x^{0}_k}\frac{f(x^{0}_1,\dots,x_k,\dots,x^{0}_n)-f(x^0)}{x_k-x^{0}_k}\triangleq\frac{\partial{f(x^0)}}{\partial{x_k}}
quindi il risultato:
L_k=\frac{\partial{f(x^0)}}{\partial{x_k}}\\[1.5em]c.v.d.
In definitiva si definisce differenziale nel punto x0=(x01,x02,…,x0k,…,x0n)T di una funzione f(x1,x2,…,xk,…,xn) calcolato sull’incremento x-x0 la forma lineare:
df_{x_0}(x-x^0)=L(x-x^0)=\frac{\partial{f(x^0)}}{\partial{x_1}}(x_1-x^{0}_1)+\dots+\frac{\partial{f(x^0)}}{\partial{x_n}}(x_n-x^{0}_n)
e quindi per ispezione risulterà per la derivata direzionale:
\frac{\partial{f(x^0)}}{\partial{v}}=\frac{\partial{f(x^0)}}{\partial{x_1}}v_1+\dots+\frac{\partial{f(x^0)}}{\partial{x_n}}v_n
Con notazione alternativa il differenziale nel punto x0=(x01,x02,…,x0k,…,x0n)T di una funzione f(x1,x2,…,xk,…,xn) calcolato sull’incremento x-x0 può essere anche riscritto come:
df_{x_0}=\frac{\partial{f(x^0)}}{\partial{x_1}}dx_1+\dots+\frac{\partial{f(x^0)}}{\partial{x_n}}dx_n
Conseguenza geometrica di questo discorso è l’esistenza di un (iper)piano tangente. Per fissare le idee si ipotizzi una funzione a due variabili z=f(x,y), tracciarne il grafico e porsi il problema se in (x0,y0) ovvero in z0=f(x0,y0) esista o meno un piano tangente. La definizione di differenziabilità riportata vede:
f(x)=f(x^0)+L(x-x^0)+\epsilon(x)|x-x^0|
ovvero, al secondo membro, al netto di un contributo di un infinitesimo di ordine superiore, la somma di un termine costante e uno lineare – primo e secondo addendo – che in \R^3 rappresenta un piano tangente e in \R^n con n>3 identifica un iperpiano tangente al grafico nel punto x0. In sostanza in \R^{n+1} l’equazione dell’iperpiano tangente sarà pari a:
z-z^0=\frac{\partial{f(x^0)}}{\partial{x_1}}(x_1-x^{0}_1)+\frac{\partial{f(x^0)}}{\partial{x_2}}(x_2-x^{0}_2)+\dots+\frac{\partial{f(x^0)}}{\partial{x_n}}(x_n-x^{0}_n)
che in \R^3 identifica l’equazione del piano tangente che si può scrivere come:
z-z_0=\frac{\partial{f(x_0,y_0)}}{\partial{x}}(x-x_0)+\frac{\partial{f(x_0,y_0)}}{\partial{y}}(y-y_0)
Ad esempio ipotizzando la classica funzione z=f(x,y)=x2+y2 per la quale si vuole valutare il piano tangente nel punto x0=1 e y0=1. Allora applicando l’ultima formula scritta l’equazione del piano tangente nel punto indicato sarà z=2+2*(x-1)+2(y-1).
x=-3:0.1:3;
y=-3:0.1:3;
[X,Y]=meshgrid(x,y);
Z1=X.^2+Y.^2;
Z2=2+2*(X-1)+2*(Y-1);
scf();
clf();
xset("colormap",jetcolormap(64));
surf(X,Y,Z1);
surf(X,Y,Z2);
È possibile una immediata verifica utilizzando Scilab. Dopo aver aperto l’editor integrato Scinotes è sufficiente copiare le righe riportate in alto per avere il grafico in 3D della funzione e del suo piano tangente nel punto indicato come da immagine riportata di seguito.
Infine si enuncia il fondamentale teorema del differenziale totale (Analisi II) per il quale se per la f(x,y) le derivate parziali esistono in tutto un intorno di x0 e sono continue in x0 – ovvero f(x,y), come si suol dire/indicare, è una funzione di classe C1, continua e derivabile e le derivate sono ancora funzioni continue – allora f(x,y) è differenziabile in x0.
La condizione è sufficiente
Per la dimostrazione si parte dalla validità delle equazioni di Cauchy-Riemann e quindi che la funzione f(z) è derivabile. Ma c’è di più, vengono ipotizzate continue le derivate prime parziali ∂u/∂x, ∂u/∂y, ∂v/∂x, ∂v/∂y allora per il teorema del differenziale totale questo vuol dire che le funzioni u(x,y) e v(x,y), cioè che la f(z) è differenziabile nell’intorno del punto (x0,y0) pertanto è possibile scrivere:
f(z)=f(z_0)+f^{'}(z₀)(z-z_0)+\epsilon(z)|z-z_0|
laddove, ricordando per ipotesi la validità delle equazioni di Cauchy-Riemann, ovvero le (D2), la f'(z0) si può anche scrivere come, ricordando che z0=x0+ιy0:
f^{'}(z_0)=f^{'}(x_0,y_0)=u_x(x_0,y_0)+\imath v_x(x_0,y_0)=v_y(x_0,y_0)-\imath u_y(x_0,y_0)
Ciò che occorre dimostrare è, dalla ipotizzata differenziabilità di f(z), che:
\lim_{z \to z_0}\frac{f(z)-f(z_0)-f^{'}(z_0)(z-z_0)}{z-z_0}=0
ovvero il calcolo del limite (che per comodità di scrittura viene scisso in una coppia di limiti uno per la parte reale e uno per la parte immaginaria):
\lim_{\substack{x\to x_0\\y \to y_0}}\frac{u(x,y)+\imath v(x,y)-u(x_0,y_0)-\imath v(x_0,y_0)-[u_x(x_0,y_0)+\imath v_x(x_0,y_0)][x-x_0+\imath(y-y_0)]}{(x-x_0)+\imath(y-y_0)}\\[1.5em]=\lim_{\substack{x\to x_0\\y \to y_0}}\frac{u(x,y)-u(x_0,y_0)-u_x(x_0,y_0)(x-x_0)+v_x(x_0,y_0)(y-y_0)}{(x-x_0)+\imath(y-y_0)}+\\[1.5em]+\lim_{\substack{x\to x_0\\y \to y_0}}\imath\frac{v(x,y)-v(x_0,y_0)-v_x(x_0,y_0)(x-x_0)-u_x(x_0,y_0)(y-y_0)}{(x-x_0)+\imath(y-y_0)}
Applicando le equazioni di Cauchy-Riemann, che per ipotesi sono valide poiché si sta dimostrando la condizione sufficiente, la coppia di limiti a secondo membro si può riscrivere come:
\lim_{\substack{x\to x_0\\y \to y_0}}\frac{u(x,y)-u(x_0,y_0)-u_x(x_0,y_0)(x-x_0)-u_y(x_0,y_0)(y-y_0)}{(x-x_0)+\imath(y-y_0)}+\\[1.5em]+\lim_{\substack{x\to x_0\\y \to y_0}}\imath\frac{v(x,y)-v(x_0,y_0)-v_x(x_0,y_0)(x-x_0)-v_y(x_0,y_0)(y-y_0)}{(x-x_0)+\imath(y-y_0)}
Ora, poiché per definizione f(z) è differenziabile in z0 allora saranno differenziabili nel punto (x0,y0) anche le funzioni u(x,y) e v(x,y) pertanto è possibile scrivere:
u(x,y)=u(x_0,y_0)+u_x(x_0,y_0)(x-x_0)+u_y(x_0,y_0)(y-y_0)+\epsilon^{u}(x,y)|x-x_0,y-y_0|\\[1.2em]v(x,y)=v(x_0,y_0)+v_x(x_0,y_0)(x-x_0)+v_y(x_0,y_0)(y-y_0)+\epsilon^{v}(x,y)|x-x_0,y-y_0|
ovvero:
u(x,y)-u(x_0,y_0)-u_x(x_0,y_0)(x-x_0)-u_y(x_0,y_0)(y-y_0)=\epsilon^{u}(x,y)|x-x_0,y-y_0|\\[1.2em]v(x,y)-v(x_0,y_0)-v_x(x_0,y_0)(x-x_0)-v_y(x_0,y_0)(y-y_0)=\epsilon^{v}(x,y)|x-x_0,y-y_0|
pertanto calcolare la coppia di limiti riportata sopra equivale a calcolare:
\lim_{(x,y)\to (x_0,y_0)}\frac{\epsilon^{u}(x,y)|x-x_0,y-y_0|+\imath\epsilon^{v}(x,y)|x-x_0,y-y_0|}{(x-x_0)+\imath(y-y_0)}
Ricordando che:
|x-x_0,y-y_0|=\sqrt{(x-x_0)^2+(y-y_0)^2}=|x-x_0+\imath(y-y_0)|
allora moltiplicando e dividendo per il modulo il limite può essere riscritto come:
\lim_{(x,y)\to (x_0,y_0)}\frac{\epsilon^{u}(x,y)|x-x_0,y-y_0|+\imath\epsilon^{v}(x,y)|x-x_0,y-y_0|}{|(x-x_0)+\imath(y-y_0)|}\times\frac{|(x-x_0)+\imath(y-y_0)|}{(x-x_0)+\imath(y-y_0)}
ma per (x,y)→(x0,y0) il secondo fattore è di valore limitato mentre il primo fattore tende a 0 per definizione di infinitesimi di ordine suoperiore pertanto il prodotto di una quantità limitata per una che tende a 0 comporta che il limite tende a 0 e quindi è uguale a 0 il limite:
\lim_{z \to z_0}\frac{f(z)-f(z_0)-f^{'}(z_0)(z-z_0)}{z-z_0}\\[1.5em]c.v.d.
Formule di Gauss-Green nel piano
Il teorema mette in relazione gli integrali di linea di seconda specie (che da un punto di vista fisico identificano il lavoro di un campo F per far muovere una particella su un cammino chiuso) e l’integrale doppio avente per dominio di integrazione la regione racchiusa dal precedente cammino chiuso.
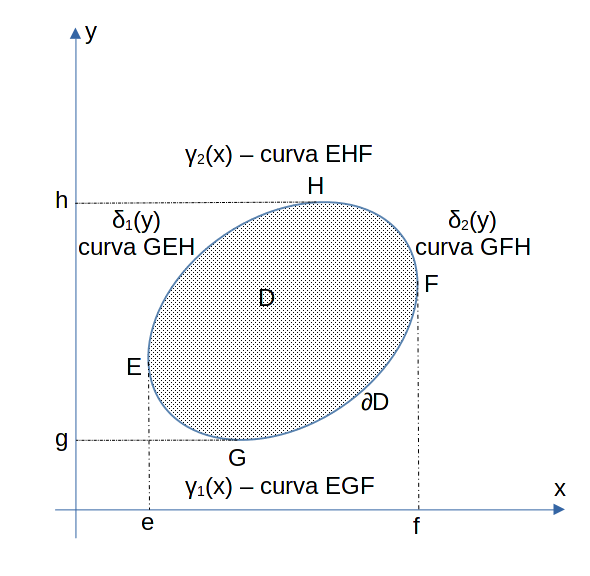
Ipotesi: Sia D un dominio semplicemente connesso nel piano – immagine in alto – nel quale si ipotizza che le parallele delle coordinate agli assi intersechino il dominio in un solo punto. Si ipotizza, inoltre, che la frontiera ∂D del suddetto dominio D sia rappresentabile con apposite curve regolari γ1(x) e γ2(x) e che tali curve siano inoltre funzioni di classe C1 in [e,f]; possiamo immaginarle come le curve che viste insieme formano la curva chiusa del contorno ∂D, ad esempio EGF per la γ1(x) e EHF per la γ2(x). Siano inoltre P(x,y) e Q(x,y) due funzioni di classe C1 – quindi, come le precedenti, continue e derivabili e le cui derivate siano ancora delle funzioni continue – definite in D e su ∂D.
Tesi: sotto le ipotesi viste si può dimostrare che sussite la seguente fondamentale relazione:
\iint\limits_{D}\left( \frac{\partial{Q(x,y)}}{\partial{x}}- \frac{\partial{P(x,y)}}{\partial{y}} \right)dxdy=\int_{\partial D}Q(x,y)dy+P(x,y)dx
Dimostrazione: il risultato può essere ottenuto per passi, i.e. dapprima considerando un dominio normale rispetto all’asse delle x quindi un dominio normale rispetto all’asse delle y seguito da un dominio normale rispetto ad entrambi gli assi ed infine per un dominio generale. Nello scenario in questione di interesse è l’ipotizzare che la regione D⊂ℜ2 sia un dominio semplicemente connesso come da definizione data in precedenza. Sotto le ipotesi viste è possibile allora scrivere:
D=\{(x,y)\isin\Reals^2 \vert \space e\le x \le f\text{ , } \gamma_1(x)\le y\le \gamma_2(x) \}
laddove le funzioni γ1(x) e γ2(x) sono le funzioni con le proprietà definite nelle ipotesi. Come primo passo, facendo uso delle formule (teorema) di riduzione di un integrale doppio a due integrali semplici (Analisi II) nella prima uguaglianza in basso e successivamente per il teorema fondamentale del calcolo integrale e alcune proprietà degli integrali, è possibile scrivere:
\iint\limits_{D}\frac{\partial{P(x,y)}}{\partial{y}}dxdy=\int_{x=e}^{x=f}\left[\int_{y=\gamma_1(x)}^{y=\gamma_2(x)}\frac{\partial{P(x,y)}}{\partial{y}}dy \right]dx=\\[1.5em]=\int_{x=e}^{x=f} P(x,y)\vert_{y=\gamma_1(x)}^{y=\gamma_2(x)}dx=\int_{x=e}^{x=f}[P(x,\gamma_2(x))-P(x,\gamma_1(x))]dx=\\[1.5em]=\int_{x=e}^{x=f}P(x,\gamma_2(x))dx-\int_{x=e}^{x=f}P(x,\gamma_1(x))dx=\\[1.5em]=-\int_{x=f}^{x=e}P(x,\gamma_2(x))dx-\int_{x=e}^{x=f}P(x,\gamma_1(x))dx=-\oint_{\partial D}P(x,y)dx
in definitiva:
\oint_{\partial D}P(x,y)dx=-\iint\limits_{D}\frac{\partial{P(x,y)}}{\partial{y}}dxdy
Analogamente se si ipotizza che il contorno ∂D del dominio D sia rappresentabile con apposite curve regolari δ1(y) e δ2(y) e che tali curve siano inoltre funzioni di classe C1 in [g,h]; possiamo immaginarle come le curve che viste insieme formano la curva chiusa del contorno ∂D, ad esempio GEH per la δ1(y) e GFH per la δ2(y), ovvero:
D=\{(x,y)\isin\Reals^2 \vert \space \delta_1(y)\le x \le \delta_2(y)\text{ , } g\le y\le h \}
Con analoga procedura e applicando medesimi teoremi e proprietà si può scrivere:
\iint\limits_{D}\frac{\partial{Q(x,y)}}{\partial{x}}dxdy=\int_{y=g}^{y=h}\left[\int_{x=\delta_1(y)}^{x=\delta_2(y)}\frac{\partial{Q(x,y)}}{\partial{x}}dx \right]dy=\\[1.5em]=\int_{y=g}^{y=h} Q(x,y)\vert_{x=\delta_1(y)}^{x=\delta_2(y)}dy=\int_{y=g}^{y=h}[Q(\delta_2(y),y)-Q(\delta_1(y),y)]dy=\\[1.5em]=\int_{y=g}^{y=h}Q(\delta_2(y),y)dy-\int_{y=g}^{y=h}Q(\delta_1(y),y)dy=\\[1.5em]=\int_{y=g}^{y=h}Q(\delta_2(y),y)dy+\int_{y=h}^{y=g}Q(\delta_1(y),y)dy=\oint_{\partial D}Q(x,y)dy
in definitiva:
\oint_{\partial D}Q(x,y)dy=\iint\limits_{D}\frac{\partial{Q(x,y)}}{\partial{x}}dxdy
Sommando i due risultati membro a membro si ottiene la tesi:
\int_{\partial D}Q(x,y)dy+P(x,y)dx=\iint\limits_{D}\left( \frac{\partial{Q(x,y)}}{\partial{x}}- \frac{\partial{P(x,y)}}{\partial{y}} \right)dxdy\\[1.5em]c.v.d.
Teorema integrale di Cauchy
Ipotesi: sia f(z) una funzione definita in Γ sottoinsieme del campo complesso e a valori nel campo complesso f:\Gamma\subseteq\Complex\Rightarrow\Complex e sia f(z) analitica in Γ∪∂Γ. Sia inoltre f(z) dotata di derivata f‘(z) continua in tutti i punti di una linea semplice chiusa γ e in tutti i punti interni ad essa.
Tesi: sotto le condizioni indicate risulta
\oint_{\gamma}f(z)dz=0
Dimostrazione: poiché si è ipotizzata f(z) analitica in Γ∪∂Γ vale la condizione di analiticità espressa dalle formule di Cauchy-Riemann:
\left \{ \begin{array}{ll} \frac{\partial{u}}{\partial{x}}=\frac{\partial{v}}{\partial{y}} \\ \frac{\partial{u}}{\partial{y}}=-\frac{\partial{v}}{\partial{x}} \end{array} \right.
Premesso questo, con ovvie sostituzioni, è possibile scrivere:
\oint_{\gamma}f(z)dz=\oint_{\gamma}[u(x,y)+\imath v(x,y)](dx+\imath dy)=\\[1.5em]=\oint_{\gamma}[u(x,y)dx-v(x,y)dy]+\imath [v(x,y)dx + u(x,y)dy]
Per le proprietà degli integrali, l’ultimo integrale può essere visto come la somma algebrica di 4 integrali distinti ai quali è possibile applicare le precedenti formule di Gauss-Green fornendo come risultato, nell’ordine in cui si succedono da sinistra verso destra:
\oint_{\gamma}u(x,y)dx=-\iint_{D}\frac{\partial{u(x,y)}}{\partial{y}}dxdy \space \text{ ; } -\oint_{\gamma}v(x,y) dy=\iint_{D}\frac{\partial{v(x,y)}}{\partial{x}}dxdy
\oint_{\gamma}v(x,y) dx=-\iint_{D}\frac{\partial{v(x,y)}}{\partial{y}}dxdy \space \text{ ; } \oint_{\gamma}u(x,y) dy=\iint_{D}\frac{\partial{u(x,y)}}{\partial{x}}dxdy
che sostituite forniscono, semplificando in un secondo momento, per motivi di spazio, la notazione:
\oint_{\gamma}f(z)dz=\oint_{\gamma}[u(x,y) dx-v(x,y) dy]+\imath [v(x,y) dx + u(x,y) dy]=\\[1.5em]=\left [-\iint_{D}\frac{\partial{u}}{\partial{y}}dxdy-\iint_{D}\frac{\partial{v}}{\partial{x}}dxdy \right]+\imath \left[-\iint_{D}\frac{\partial{v}}{\partial{y}}dxdy+\iint_{D}\frac{\partial{u}}{\partial{x}}dxdy \right]
Sostituendo in esse le formule di Cauchy-Riemann risulta:
\left [\cancel{\iint_{D}\frac{\partial{u}}{\partial{y}}dxdy} \cancel{-\iint_{D}\frac{\partial{u}}{\partial{y}}dxdy} \right]+\imath \left[-\cancel{\iint_{D}\frac{\partial{v}}{\partial{y}}dxdy}+\cancel{\iint_{D}\frac{\partial{v}}{\partial{y}}dxdy} \right]
il che implica la tesi ovvero:
\oint_{\gamma}f(z)dz=0
Questo risultato comporta che se una funzione è analitica, secondo la definizione precedentemente data, in una regione semplicemente connessa (ovvero in una regione del piano complesso nella quale si può passare con continuità da una curva congiungente due punti qualsiasi ad un’altra curva congiungente i due stessi punti ma diversa dalla curva precedente, in sostanza quando nella regione non vi sono “buchi” nel qual caso viene definita molteplicemente connessa) allora l’integrale esteso a qualsiasi curva chiusa contenuta nella suddetta regione è nullo. In conseguenza di ciò per tutti i percorsi di una regione nei quali la funzione è analitica l’integrale assume sempre lo stesso valore.

Questo significa che è possibile “deformare” il cammino di integrazione esterno ∂Γ in uno più noto e facilmente descrivibile – e.g. una circonferenza γ – a patto che ci si muova sempre all’interno di una regione di analiticità per la funzione f(z). Cammino di integrazione sul quale è possibile calcolare più facilmente l’integrale il quale, per il teorema appena dimostrato, in una curva chiusa all’interno della regione di analiticità assumerà lo stesso valore che ha sul contorno esterno, ovvero con riferimento alla figura in alto:
\oint_{+\partial\Gamma}f(z)dz=\oint_{\gamma}f(z)dz
come da dimostrazione del teorema (conseguenza) che segue.
Conseguenza del teorema di Cauchy
Una conseguenza del teorema di Cauchy – in realtà se ne potrebbe dimostrare più di una, ma verrà riportata solo quella di interesse per l’argomento in questione – riguarda le regioni molteplicemente connesse sul calcolo dell’integrale di linea, conseguenza utilizzata nel seguito per arrivare a giustificare analiticamente il criterio di Nyquist.
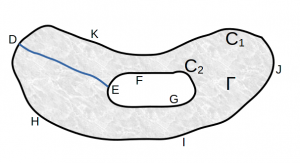
Sia Γ una regione limitata dalle due linee semplici chiuse C1 e C2 e sia f(z) analitica in Γ e su C1 e C2 (figura in alto). Si dimostra che:
\oint_{C_1} f(z)dz=\oint_{C_2} f(z)dz
dove C1 e C2 sono percorse entrambe in verso positivo (antiorario) secondo la definizione riportata in precedenza.
Dimostrazione: data la regione molteplicemente connessa visibile in figura dopo aver operato il taglio DE può essere applicato il teorema di Cauchy dimostrato al passo precedente e in base al quale è possibile scrivere:
\int\limits_{DEFGEDHIJKD}f(z)dz=0
Le tipiche e note proprietà degli integrali portano a scrivere la precedente come:
\cancel{\int\limits_{DE}f(z)dz}+\int\limits_{EFGE}f(z)dz+\cancel{\int\limits_{ED}f(z)dz}+\int\limits_{DHIJKD}f(z)dz=0
ricordando che, per una nota proprietà di base degli integrali:
\int\limits_{DE}f(z)dz=-\int\limits_{ED}f(z)dz
Pertanto è posisbile riscrivere, ricordando la medesima proprietà:
\int\limits_{EFGE}f(z)dz+\int\limits_{DHIJKD}f(z)dz=0\\[1.5em]\int\limits_{DHIJKD}f(z)dz=-\int\limits_{EFGE}f(z)dz=\int\limits_{EGFE}f(z)dz
ovvero.
\oint_{C_1} f(z)dz=\oint_{C_2} f(z)dz \\[1.5em]c.v.d.
In termini più generali se si vuole integrare la funzione complessa f(z) lungo una curva C si può, senza alterare il risultato, sostituire alla curva C una curva generica γ con l’unica condizione che sia soddisfatta l’analiticità della funzione f(z) nella regione compresa tra le due curve chiuse e sul contorno delle stesse.
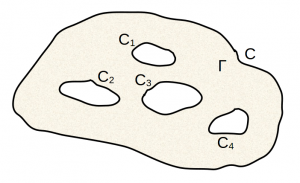
Una conseguenza del precedente teorema è il teorema successivo (la cui dimostrazione è immediata dal precedente) per il quale se f(z) è una funzione analitica nella regione limitata da un certo numero di curve chiuse semplici non sovrapposte e sul contorno delle stesse curve (e.g. immagine al lato), allora risulta:
\oint_{C}f(z)dz=\oint_{C1}f(z)dz+\oint_{C2}f(z)dz+\oint_{C3}f(z)dz+\oint_{C4}f(z)dz
Formule integrali di Cauchy
Sia f(z) una funzione analitica dentro la regione Γ semplicemente connessa e sulla sua frontiera ∂Γ ovvero in \Gamma\cup\partial\Gamma e sia z0 un punto appartenente a Γ. Sotto queste condizioni esiste la seguente prima formula integrale di Cauchy:
f(z_0)=\frac{1}{2\pi\imath}\oint_{+\partial\Gamma} \frac{f(z)}{z-z_0}dz
inoltre, come conseguenza, risulta che la derivata n-esima di f(z) in z=z0 è data da:
f^{(n)}(z_0)=\frac{n!}{2\pi\imath}\oint_{+\partial\Gamma}\frac{f(z)}{(z-z_0)^{n+1}}dz \text{ } n=1,2,3,\dots
che permette di determinare i valori di tutti i valori delle derivate della funzione f(z) all’interno della regione di analiticità. Importante conseguenza è che se una funzione f(z), con z variabile complessa, è analitica nella regione indicata – quindi se esiste la derivata prima – allora esistono nella medesima regione di analiticità tutte le sue derivate di ordine superiore. Questo risultato non è necessariamente valido per le funzioni di variabili reali.
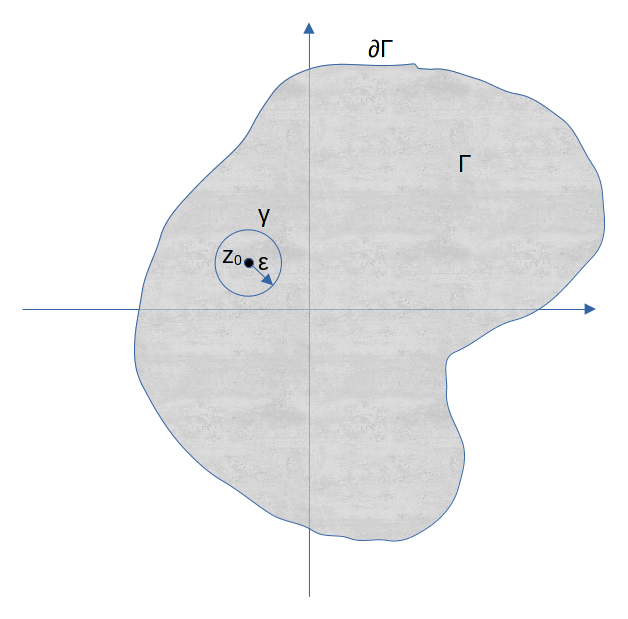
Dimostrazione: sia z0 un punto contenuto nella regione di analiticità per la f(z) e sia γ una circonferenza di raggio ε centrata in z0 secondo quanto riportato nell’immagine in alto. Dal teorema di Cauchy, poiché la regione è tutta di analiticità per la f(z), è oramai noto che calcolare l’integrale su ∂Γ equivale a calcolare l’integrale sul cerchio γ di raggio ε. In formule:
\oint_{+\partial\Gamma}\frac{f(z)}{z-z_0}dz=\oint_{\gamma}\frac{f(z)}{z-z_0}dz
Per tutti i punti z appartenenti alla circonferenza γ si può scrivere |z-z0|=ε ovvero, ricordando l’equazione parametrica del cerchio, z(θ)=z0+ε•eιθ laddove z0=x0+ιy0 e ε•eιθ sono i punti sulla circonferenza di centro z0 e raggio ε; l’argomento di ogni singolo punto è dato dal valore di θ. In base a quanto riportato allora è possibile scrivere: z(θ)-z0=ε•eιθ e dz=ε•ι•eιθ dθ che, sostituite nell’integrale a destra della precedente formula, forniscono:
\oint_{+\partial\Gamma}\frac{f(z)}{z-z_0}dz=\oint_{\gamma}\frac{f(z)}{z-z_0}dz=\int_0^{2\pi}\frac{f(z_0+\epsilon e^{\imath\theta})}{\cancel{z_0}+\cancel{\epsilon e^{\imath\theta}}-\cancel{z_0}}\imath\cancel{\epsilon e^{\imath\theta}}d\theta=\\[1.5em]=\imath\int_0^{2\pi}f(z_0+\epsilon e^{\imath\theta}) d\theta
Ma per il richiamato teorema di Cauchy l’ultimo integrale a destra dell’uguaglianza assume sempre lo stesso valore qualunque sia ε a patto che la regione di integrazione risulti ancora analitica per la funzione integranda. Pertanto è possibile scegliere ε con una certa arbitrarietà al limite anche per ε→0. È possibile pertanto scrivere, stante anche la continuità della funzione:
\oint_{+\partial\Gamma}\frac{f(z)}{z-z_0}dz=\oint_{\gamma}\frac{f(z)}{z-z_0}dz=\imath\int_0^{2\pi}f(z_0+\epsilon e^{\imath\theta}) d\theta=\\[1.5em]=\imath\int_0^{2\pi}\lim_{\epsilon\rightarrow 0}f(z_0+\epsilon e^{\imath\theta}) d\theta=\imath f(z_0)\int_0^{2\pi}d\theta=2\pi\imath f(z_0)
da cui è possibile riportare la seguente uguaglianza, considerando il primo integrale a sinistra e l’ultimo risultato ottenuto:
\oint_{+\partial\Gamma}\frac{f(z)}{z-z_0}dz=2\pi\imath f(z_0)
ovvero la tesi:
f(z_0)=\frac{1}{2\pi\imath}\oint_{+\partial\Gamma}\frac{f(z)}{z-z_0}dz\\[1.5em] c.v.d.
Cosa è possibile concludere con le formule di Cauchy? Che se si conoscono i valori che la funzione f(z) assume sul contorno della regione di analiticità – contorno sul quale la stessa f(z) è analitica – allora è possibile determinare il valore della funzione e di tutte le sue derivate in tutti i punti interni alla regione nella quale la funzione è analitica. Per dimostrare l’ultima affermazione ipotizziamo in luogo di z0 un generico punto z purché appartenente alla regione di analiticità Γ della f(z), allora la prima formula integrale di Cauchy la si può riscrivere:
f(z)=\frac{1}{2\pi\imath}\oint_{+\partial\Gamma} \frac{f(\xi)}{\xi-z}d\xi
laddove, si ricorda, che z=x+ιy pertanto è “implicita” la presenza delle variabili x e y nella formula integrale di Cauchy sopra richiamata. È possibile, pertanto, operare delle derivate parziali della f(z) rispetto a x e rispetto y i cui risultati – ricordando la derivata del rapporto di due funzioni; “numeratore derivato moltiplicato denominatore non derivato sottratto al prodotto del numeratore non derivato per il denominatore derivato tutto diviso il denominatore al quadrato” – vedono:
\frac{\partial f(x,y)}{\partial x}=\frac{\partial}{\partial x} \left [\frac{1}{2\pi\imath}\oint_{+\partial\Gamma} \frac{f(\xi)}{\xi-(x+\imath y)}d\xi \right]=\frac{1}{2\pi\imath}\oint_{+\partial\Gamma} \frac{-f(\xi)(-1)}{[\xi-(x+\imath y)]^2}d\xi=\\[1.5em]=\frac{1}{2\pi\imath}\oint_{+\partial\Gamma} \frac{f(\xi)}{(\xi-z)^2}d\xi
Derivando ora la stessa formula rispetto a ι∂y risulta:
\frac{\partial f(x,y)}{\imath\partial y}=\frac{\partial}{\imath\partial y} \left [\frac{1}{2\pi\imath}\oint_{+\partial\Gamma} \frac{f(\xi)}{\xi-(x+\imath y)}d\xi \right]=\frac{1}{\cancel{\imath}} \frac{1}{2\pi\imath}\oint_{+\partial\Gamma} \frac{-f(\xi)(-\cancel{\imath})}{[\xi-(x+\imath y)]^2}d\xi=\\[1.5em]=\frac{1}{2\pi\imath}\oint_{+\partial\Gamma} \frac{f(\xi)}{(\xi-z)^2}d\xi
L’importante risultato che le due derivate parziali valutate prima rispetto a x poi rispetto a ιy danno lo stesso risultato e eguagliando i primi membri se ne deduce che la funzione f(z) soddisfa la condizione di Cauchy-Riemann. L’espressione della derivata prima complessa della f(z) ovvero della formula integrale di Cauchy è possibile allora riscriverla:
f^{'}(z)=\frac{1}{2\pi\imath}\oint_{+\partial\Gamma} \frac{f(\xi)}{(\xi-z)^2}d\xi
Della precedente espressione è possibile valutare di nuovo la derivata parziale rispetto a x e la derivata parziale rispetto a ιy e con analogo procedimento si ottiene:
f^{''}(z)=\frac{2}{2\pi\imath}\oint_{+\partial\Gamma} \frac{f(\xi)}{(\xi-z)^3}d\xi
e così via fino alla derivata n-esima la cui espressione è possibile scriverla:
f^{n}(z)=\frac{d^nf(z)}{dz^n}=\frac{n!}{2\pi\imath}\oint_{+\partial\Gamma} \frac{f(\xi)}{(\xi-z)^{n+1}}d\xi
che determina così l’esistenza delle derivate di ogni ordine f(n)(z) per ogni valore di n e quindi implicitamente anche la dimostrazione che se la funzione f(z) soddisfa la condizione di Cauchy-Riemann allora la stessa f(z) è derivabile con ogni ordine di derivata.
Teorema di Taylor
Ipotesi: sia f(z) una funzione analitica dentro la regione Γ semplicemente connessa e sulla sua frontiera ∂Γ ovvero in \Gamma\cup\partial\Gamma. Sia z0 un punto appartenente alla regione di analiticità. Detto δ il raggio di una circonferenza centrata in z0 tutta inclusa nella regione di analiticità con al più i punti della circonferenza comuni con i punti della frontiera del dominio come da immagine riportata.
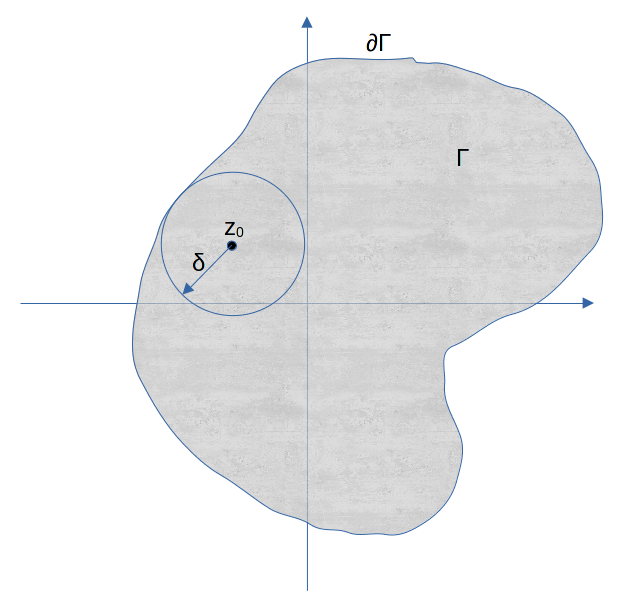
Tesi: per ogni punto z tale che |z-z0|<δ, ovvero per ogni punto che sta nella regione delimitata dalla circonferenza di centro z0 e raggio δ, risulta che:
f(z)=\sum_{n=0}^{+\infty} a_n(z-z_0)^n \text{ dove } a_n=\frac{f^{(n)}(z_0)}{n!}
con una corrispondenza della serie di Taylor nel campo reale (basti pensare x in luogo di z). Se z0=0 la serie risultante è detta sviluppo in serie di Mac Laurin.
Dimostrazione: preso un punto z appartenente alla regione delimitata dalla circonferenza sopra definita nella quale la f(z) è analitica, dalla formula integrale di Cauchy è possibile scrivere:
f(z)=\frac{1}{2\pi\imath}\oint_{+\partial\Gamma}\frac{f(\xi)}{(\xi-z)}d\xi
con il denominatore della funzione integranda pari a:
\frac{1}{\xi-z}=\frac{1}{\xi-z+z_0-z_0}=\frac{1}{(\xi-z_0)-(z-z_0)}=\\[1.5em]=\frac{1}{(\xi-z_0)}\frac{1}{1-\frac{z-z_0}{\xi-z_0}}
Preso ξ un qualunque punto appartenente alla regione di analiticità ma al di fuori della circonferenza di raggio δ, al limite sulla circonferenza, si può scrivere |ξ–z0|≥δ pertanto come conseguenza si avrà:
\left| \frac{z-z_0}{\xi-z_0} \right| = k \lt 1
e il denominatore della funzione integranda può essere riscritto come:
\frac{1}{\xi-z}=\frac{1}{\xi-z_0}\frac{1}{1-k}
ma l’ultimo termine altro non è che la somma di una serie geometrica di ragione k – convergente per |k|<1 – per la quale risulta:
\sum_{n=0}^{+\infty}k^n=\frac{1}{1-k}=\frac{1}{1-\frac{z-z_0}{\xi-z_0}}=\sum_{n=0}^{+\infty} \left(\frac{z-z_0}{\xi-z_0} \right)^n
quindi:
\frac{1}{(\xi-z_0)}\frac{1}{1-\frac{z-z_0}{\xi-z_0}}=\sum_{n=0}^{+\infty} \frac{(z-z_0)^n}{(\xi-z_0)^{n+1}}
che sostituita nella formula integrale di Cauchy precedentemente scritta fornisce, osservando che la variabile di integrazione è ξ e non z:
f(z)=\frac{1}{2\pi\imath}\oint_{+\partial\Gamma}\frac{f(\xi)}{(\xi-z)}d\xi=\oint_{+\partial\Gamma}f(\xi)\sum_{n=0}^{+\infty} \frac{(z-z_0)^n}{(\xi-z_0)^{n+1}}d\xi=\\[1.5em]=\sum_{n=0}^{+\infty} \underbrace{\frac{1}{2\pi\imath} \left[\oint_{+\partial\Gamma}\frac{f(\xi)}{(\xi-z_0)^{n+1}}d\xi \right]}_{a_n} (z-z_0)^n=\sum_{n=0}^{+\infty}a_n (z-z_0)^n\\[1.5em]c.v.d.
Ma una conseguenza della formula integrale di Cauchy ha dato come risultato che:
f^{(n)}(z_0)=\frac{n!}{2\pi\imath}\oint_{+\partial\Gamma}\frac{f(z)}{(z-z_0)^{n+1}}dz
ed avendo posto:
a_n=\frac{1}{2\pi\imath} \oint_{+\partial\Gamma}\frac{f(\xi)}{(\xi-z_0)^{n+1}}d\xi
allora per ispezione con la precedente è evidente come risulti:
a_n=\frac{f^{(n)}(z_0)}{n!}
risultando così dimostrata anche la seconda affermazione ottenendo così la formula dello sviluppo in serie di Taylor già noto (Analisi I) in ambito reale, qui esteso nell’ambito di una funzione complessa:
f(z)=\sum_{n=0}^{+\infty}\frac{f^{(n)}(z_0)}{n!}(z-z_0)^n=\\[1.5em]=f(z_0)+f^{'}(z_0)(z-z_0)+\frac{f^{''}(z_0)}{2!}(z-z_0)^2+ \dots +\frac{f^{(n)}(z_0)}{n!}(z-z_0)^n+ \dots
Teorema di Laurent
L’obiettivo è uno sviluppo in serie di potenze ma con esponenti tanto positivi quanto negativi. Il contesto di sviluppo morfologicamente vede una corona circolare di centro z0 e raggi r1 e r2 tale che r1<|z-z0|<r2 – come da immagine riportata di seguito – e nella quale una funzione f(z) risulti analitica in essa.
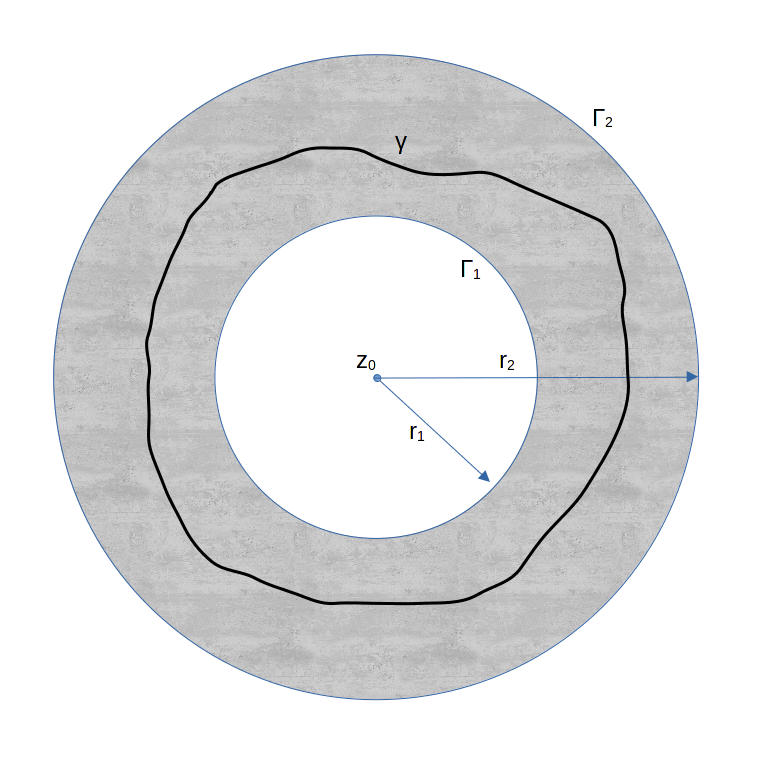
Ipotesi: sotto le condizioni riportate preso un qualunque punto z appartenente ad una linea chiusa γ circondante z0 che si estende nella regione delimitata dalla corona circolare e lungo la quale la fuznione f(z) è analitica, quindi tale che r1<|z-z0|<r2;
Tesi: allora è possibile scrivere la funzione f(z) come (ricordando la definizione di serie doppiamente infinite):
f(z)=\sum_{n=-\infty}^{+\infty}c_n(z-z_0)^n=\sum_{n=0}^{+\infty}c_n(z-z_0)^n+\sum_{n=1}^{+\infty}c_{-n}(z-z_0)^{-n}
esplicitabile come:
f(z)= \dots +\frac{c_{-n}}{(z-z_0)^n}+\dots +\frac{c_{-1}}{(z-z_0)}+c_0+c_1(z-z_0)+\dots +c_n(z-z_0)^n+\dots
laddove i coefficienti per ogni valore di n è possibile rappresentarli:
c_n=\frac{1}{2\pi\imath}\oint_\gamma \frac{f(\xi)}{(\xi-z_0)^{n+1}}d\xi
formalmente analoga ai coefficienti an visti in precedenza solo che in questo caso i valori di n sono positivi e negativi. Ma in quest’ultimo caso occorre fare attenzione poiché non è detto che esistano le derivate n-esime della f(ξ) poichè questa condizione era valida solo per n positivi e f(ξ) analitica in z0 , ma nessuna di queste condizioni sono verificate – o quanto meno ipotizzate – nella definizione del teorema di Laurent!
Dimostrazione: presi due punti ξ1 e ξ2 appartenenti al contorno delle due circonferenze della corona circolare e considerando la f(z) come la somma delle due sommatorie precedentemente riportate, allora applicando la formula integrale di Cauchy è possibile scrivere:
f(z)=\frac{1}{2\pi\imath}\left[\oint_{+\partial\Gamma 1}\frac{f(\xi_1)}{\xi_1-z}d\xi 1- \oint_{+\partial\Gamma 2}\frac{f(\xi_2)}{\xi_2-z}d\xi 2 \right]
Nel primo integrale il denominatore della funzione integranda è stato già affrontato nel teorema di Taylor pertanto viene focalizzata l’attenzione sul denominatore della funzione integranda del secondo integrale. Con analogo procedimento si può scrivere:
-\frac{1}{\xi_2-z}=\frac{1}{-\xi_2+z+z_0-z_0}=\frac{1}{-(\xi_2-z_0)+(z-z_0)}=\\[1.5em]=\frac{1}{z-z_0}\frac{1}{1-\left( \frac{\xi_2-z_0}{z-z_0} \right)}=\sum_{n=0}^{+\infty}\frac{(\xi_2-z_0)^n}{(z-z_0)^{n+1}}
ponendo m=n+1 si ha che n=m-1 che sostituito nella sommatoria fornisce:
\sum_{n=0}^{+\infty}\frac{(\xi_2-z_0)^n}{(z-z_0)^{n+1}}= \sum_{n=0}^{+\infty}\frac{(z-z_0)^{-n-1}}{(\xi_2-z_0)^{-n}}=\sum_{m=1}^{+\infty}\frac{(z-z_0)^{-m}}{(\xi_2-z_0)^{-m+1}}
Sostituendo le due serie nei due integrali:
f(z)=\frac{1}{2\pi\imath} \left[\oint_{+\partial\Gamma 1}\frac{f(\xi_1)}{(\xi_1-z)}d\xi_1- \oint_{+\partial\Gamma 2}\frac{f(\xi_2)}{(\xi_2-z)}d\xi_2\right]=\\[1.5em]=\frac{1}{2\pi\imath}\left\{ \oint_{+\partial\Gamma 1}\left[f(\xi_1) \sum_{n=0}^{+\infty}\frac{(z-z_0)^n}{(\xi 1-z_0)^{n+1}}\right]d\xi_1 + \oint_{+\partial\Gamma 2}\left[f(\xi_2) \sum_{m=1}^{+\infty}\frac{(z-z_0)^{-m}}{(\xi_2-z_0)^{-m+1}}\right] d\xi_2 \right\}=\\[1.5em]=\sum_{n=0}^{+\infty}\underbrace{\left[\frac{1}{2\pi\imath}\oint_{+\partial\Gamma 1}\frac {f(\xi_1)} {(\xi_1-z_0)^{n+1}} d\xi_1 \right]}_ {c_n}(z-z_0)^n+\sum_{m=1}^{+\infty}\underbrace{\left[\frac{1}{2\pi\imath}\oint_{+\partial\Gamma 2}\frac {f(\xi_2)} {(\xi_2-z_0)^{-m+1}} d\xi_2 \right]}_ {c_{-n}}(z-z_0)^{-m}
cioè, analogamente al teorema di Taylor, la tesi per la quale la prima serie viene definita parte analitica dello sviluppo di Laurent e la si indica con:
I_1(z)=\sum_{n=0}^{+\infty} c_n(z-z_0)^n
e la seconda serie come parte singolare dello sviluppo di Laurent e la si indica con:
I_2(z)=\sum_{m=1}^{+\infty} c_{-n}(z-z_0)^{-m}
In definitiva:
f(z)=I_1(z)+I_2(z)=\sum_{n=0}^{+\infty} c_n(z-z_0)^n+\sum_{m=1}^{+\infty} c_{-n}(z-z_0)^{-m}\\[1.5em]c.v.d.
Singolarità
Definizione: Sia f(z) una funzione analitica nella solita regione Γ. Si dirà che un punto z0 è un punto singolare se:
- f(z) non è analitica quando calcolata in z0;
- in ogni intorno del punto z0 esiste un punto diverso da z0 dove la f(z) è analitica.
Il punto z0 è una singolarità isolata per f(z) se ∃Iδ(z0)| |z-z0|=Iδ(z0) che non racchiuda punti singolari diversi da z0, altrimenti detto se rimuoviamo dall’intorno δ il punto z0 non dovranno esistere altri punti di singolarità. Se è impossibile determinare un intorno circolare allora la singolarità è detta singolarità non isolata. Si definisce singolarità eliminabile un punto z0 per il quale esiste determinato e finito il limite della funzione f(z) per z→z0 cioè:
\lim_{z\to z_0}f(z)=\text{esiste ed ha valore finito}
Una singolarità che non rientra nelle precedenti definizioni è detta singolarità essenziale.
Nell’ambito delle singolarità occorre osservare come lo sviluppo in serie di Laurent presenti termini aggiuntivi rispetto ai termini dello sviluppo in serie di Taylor del tipo:
\frac{c_{-n}}{(z-z_0)^n}
Dai risultati fin qui ottenuti se i coefficienti c-n relativi a tali termini sono tutti nulli per n≤-1 allora la funzione f(z) è analitica in z0 e la serie di Laurent si riduce alla serie di Taylor. In caso contrario si dice che la funzione f(z) in z0 presenta un punto singolare (o singolarità) detto polo se la serie di Laurent ha un numero finito di termini altrimenti, in presenza di infiniti termini, si è in presenza di una singolarità essenziale. Questo significa che è possibile classificare le singolarità analizzando lo sviluppo in serie di Laurent della funzione f(z).
Supponiamo, ad esempio, che il generico punto z0 sia una singolarità isolata per la funzione f(z) ovvero che ∃Iδ(z0)|f(z) risulti analitica in Γ-{z0}. In pratica implica dire che si riuscirà a costruire attorno al punto z0 un cerchietto dove l’unico punto singolare è lo stesso z0.
Occorre osservare che più ci si avvicina ad una singolarità, ovvero per z→z0, tanto più una funzione analitica tende ad aumentare indefinitamente. Infatti preso il punto singolare z0 e sviluppando la f(z) in serie di Laurent si avrebbe:
f(z)=\sum_{n=-\infty}^{+\infty}c_n(z-z_0)^n
i cui coefficienti hanno l’espressione precedentemente ricavata. In particolare prendendo il coefficiente con valore generico -n è possibile scrivere:
c_{-n}=\frac{1}{2\pi\imath}\oint_{+\partial\Gamma}\frac{f(\xi)}{(z-z_0)^{-n+1}}d\xi
e considerandone il modulo:
|c_{-n}|=\left|\frac{1}{2\pi\imath}\oint_{+\partial\Gamma}\frac{f(\xi)}{(z-z_0)^{-n+1}}d\xi \right|\le\frac{1}{2\pi}\oint_{+\partial\Gamma}|z-z_0|^{n-1}|f(\xi)||d\xi |
Essendo |z-z0|=r se ipotizzassimo per assurdo che fissato un valore massimo M risulti |f(ξ)|<M allora dalla precedente:
|c_{-n}|\le\frac{1}{2\pi}r^{n-1}M\oint_{+\partial\Gamma} d\xi=\frac{1}{2\pi}r^{n-1}M\int_{0}^{2\pi} d\xi=Mr^n
ma poiché r può essere reso piccolo a piacere allora ecco che risulterebbe c-n=0, c-n+1=0, … c-2=0 e c-1=0 ovvero la serie di Laurent si riduce alla serie di Taylor venendosi così ad annullare la parte singolare della serie di Laurent. Questo implica che la f(z) in z=z0 viene ad essere analitica contro l’ipotesi inziale che vedeva z0 essere una singolarità per la f(z). La contraddizione è nata dall’aver ipotizzato la f(z) limitata da un valore massimo M. Ovvia conclusione la f(z) non può essere limitata nell’intorno di una singolarità.
c.v.d.
Si supponga ora che lo sviluppo in serie di Laurent presenti N termini per la f(z) nella parte singolare il che, è lo stesso, si possa scrivere come:
I_2(z)=a_{-N}(z-z_0)^{-N}+a_{-N+1}(z-z_0)^{-N+1}+\dots +a_{-2}(z-z_0)^{-2}+a_{-1}(z-z_0)^{-1}
che in forma abbreviata può essere riscritta, ricordando la parte analitica dello sviluppo di Laurent, come f(z)=I1(z)+I2(z). Se indichiamo con g(z) lo sviluppo in serie di Taylor ovvero:
g(z)=I_1(z)=\sum_{n=0}^{+\infty}a_n(z-z_0)^n
allora la f(z) la si può riscrivere come:
f(z)=g(z)+a_{-N}(z-z_0)^{-N}+\dots +a_{-2}(z-z_0)^{-2}+a_{-1}(z-z_0)^{-1}
che moltiplicata al primo e secondo membro per (z-z0)N fornisce:
(z-z_0)^N f(z)=g(z)(z-z_0)^N+a_{-N}+\dots +a_{-2}(z-z_0)^{N-2}+a_{-1}(z-z_0)^{N-1}
Ma la parte a destra dell’uguaglianza esprime lo sviluppo in serie di Taylor poiché presenta solo esponenti positivi e pertanto i termini esprimono una funzione analitica. Allora passando al limite di z→z0 il risultato fondamentale:
\lim_{z\to z_0}(z-z_0)^N f(z)=a_{-N}\neq 0
ovvero chiamando F(z)=f(z)(z-z0)N è ovvio come F(z0)≠0 e pertanto la F(z) è una funzione definita dove è definita la f(z), è analitica dove lo è la f(z). Allora quando la f(z) presenta un polo, nello specifico di ordine generico N, la si può scrivere come:
f(z)=\frac{F(z)}{(z-z_0)^N}
con F(z) analitica in z0 e F(z0)≠0.
Alcuni casi di massima vedono:
- Se f(z) è analitica in z0 e risulta f(z0)≠0 allora lo sviluppo in serie di Laurent assumerà la forma:
f(z)=\sum_{n=0}^{+\infty}c_n(z-z_0)^n \text { con }c_0\neq0\text { e }c_n=0 \text { }\forall n\leq -1 - Se f(z) è analitica in z0 e f(z0)=0 con molteplicità N>0 allora lo sviluppo in serie di Laurent non può partire da un indice negativo e nemmeno da 0 ma non potrà che partire da un indice positivo pari a N, in sostanza:
f(z)=\sum_{n=N}^{+\infty}c_n(z-z_0)^n\text { con }c_N\neq0\text { e }c_n=0 \text { }\forall n\lt N - Se f(z) è analitica in Γ∪∂Γ-{z0}, in presenza di un polo del primo ordine in z0 lo sviluppo in serie di Laurent può essere scritto come:
f(z)=\sum_{n=-1}^{+\infty}c_n(z-z_0)^n \text { con }c_1\neq0\text { e }c_n=0 \text { }\forall n\lt -1 - E, in modo ancora più generico, se f(z) è analitica in Γ∪∂Γ-{z0}, in presenza di un polo di ordine N≥1 in z0 lo sviluppo in serie di Laurent può essere scritto come:
f(z)=\sum_{n=-N}^{+\infty}c_n(z-z_0)^n \text { con }c_{-N}\neq0\text { e }c_n=0 \text { }\forall n\lt -N
Residui e teorema dei Residui
Definizione: sia f(z) una funzione analitica in una regione Γ e sul suo contorno ∂Γ e sia z0 una singolarità isolata. Per questa funzione, in base ai risultati fin qui ottenuti, è possibile affermare che f(z) è sviluppabile in serie di Laurent ovvero:
f(z)=\sum_{n=-\infty}^{+\infty}c_n(z-z_0)^n
valida per ogni punto z tale che r1<|z-z0|<r2 ovvero compreso in una corona circolare delimitata da due circonferenze di raggio r1 e r2, laddove non ci siano altre singolartà oltre a z0 e i cui coefficienti sono uguali a:
c_n=\frac{1}{2\pi\imath}\oint_{+\partial\Gamma}\frac{f(\xi)}{(\xi-z_0)^{n+1}}d\xi
Nel caso particolare di n=-1 si ottiene banalmente:
c_{-1}=\frac{1}{2\pi\imath}\oint_{+\partial\Gamma}f(\xi)d\xi
ovvero il primo coefficiente della parte singolare dello sviluppo in serie di Laurent; tale coefficiente prende il nome di residuo della funzione f(z) nella singolarità z0 e lo si indica in genere con Res.(f,z0) oppure con Rf(z) (z0)=c-1.
Vale il seguente fondamentale teorema dei Residui.
Ipotesi: sia f(z) una funzione analitica in Γ e sulla sua frontiera ∂Γ ad eccezione di un certo numero di punti z1, z2, …, zn con residui noti e pari a c1-1, c2-1 , …, cn-1;
Tesi: allora il teorema dei Residui afferma che:
\frac{1}{2\pi\imath}\oint_{+\partial\Gamma}f(\xi)d\xi=\sum_{k=1}^{n}Res.(f,z_k)
ovvero che l’integrale di f(z) calcolato lungo la frontiera ∂Γ è uguale a 2πι volte la somma dei residui della f(z) delle singolarità racchiuse in ∂Γ.
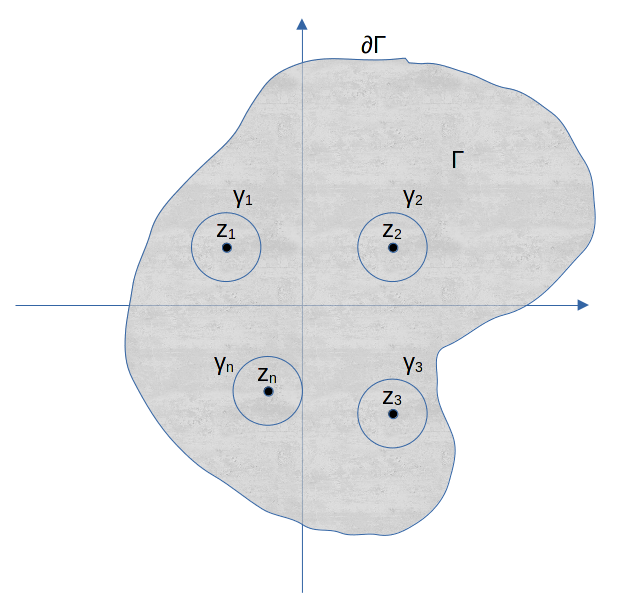
Dimostrazione: costruiti i soliti cerchi (immagine in alto) attorno alle singolarità, per il teorema di Cauchy e sua conseguenza e ricordando la proprietà di additività degli integrali, si può scrivere (i segni negativi sono dati dal fatto che la percorrenza dei cerchi attorno alle singolarità avvengono in senso inverso; antiorario sulla curva Γ per lasciarsi alla sinistra la regione, e in senso orario per le curve γi con i=1,2,…,n):
\frac{1}{2\pi\imath}\oint_{+\partial\Gamma}f(\xi)d\xi-\frac{1}{2\pi\imath}\oint_{\gamma 1}f(\xi)d\xi-\frac{1}{2\pi\imath}\oint_{\gamma 2}f(\xi)d\xi- \dots -\frac{1}{2\pi\imath}\oint_{\gamma n}f(\xi)d\xi=0
ovvero:
\frac{1}{2\pi\imath}\oint_{+\partial\Gamma}f(\xi)d\xi=\frac{1}{2\pi\imath}\oint_{\gamma 1}f(\xi)d\xi+\frac{1}{2\pi\imath}\oint_{\gamma 2}f(\xi)d\xi+ \dots +\frac{1}{2\pi\imath}\oint_{\gamma n}f(\xi)d\xi=\\[1.5em]=\frac{1}{2\pi\imath} \left[ \oint_{\gamma 1}f(\xi)d\xi+\oint_{\gamma 2}f(\xi)d\xi+ \dots +\oint_{\gamma n}f(\xi)d\xi \right]=\frac{1}{2\pi\imath}\sum_{k=1}^{n}\oint_{\gamma_k}f(\xi)d\xi
Ma dai coefficienti degli sviluppi in serie di Laurent prendendo il valore n=-1 risulta:
c_{-1}=\frac{1}{2\pi\imath}\oint_{\gamma}f(\xi)d\xi
allora tenendo conto del precedente risultato, osservando come ogni addendo tra parentesi quadre altro non è che il residuo della funzione calcolato nel punto singolare presente nel dominio di calcolo dell’integrale, è possibile scrivere:
\frac{1}{2\pi\imath}\oint_{+\partial\Gamma}f(\xi)d\xi=[c_{-1}^1+c_{-1}^2+\dots +c_{-1}^{n-1}+c_{-1}^n ]
laddove c1-1 è il residuo della funzione f(z) in z1, c2-1 il residuo della f(z) in z2 e così via quindi si può scrivere:
\frac{1}{2\pi\imath}\oint_{+\partial\Gamma}f(\xi)d\xi=\sum_{k=1}^{n}Res.(f,z_k)\\[1.5em]c.v.d.
Nella realtà il calcolo pratico dei residui viene fatto senza necessità alcuna di ricorrere agli integrali ma la risoluzione avviene tramite un calcolo algebrico. Ad esempio se z0 è un polo del primo ordine per la f(z) allora per quanto fin qui appreso dallo sviluppo in serie di Laurent è possibile scrivere:
f(z)=\sum_{n=0}^{+\infty}c_n(z-z_0)^n+\frac{c_{-1}}{z-z_0}
e moltiplicando 1° e 2° membro per z-z0 ottenere:
(z-z_0)f(z)=\sum_{n=0}^{+\infty}c_n(z-z_0)^{n+1}+c_{-1}
e per z→z0 si ottiene la formula per un polo del primo ordine:
\lim_{z\to z_0}(z-z_0)f(z)=c_{-1}=Res.(f,z_0)
Generalizzandola per un polo di ordine m lo sviluppo in serie di Laurent per la f(z) fornisce:
f(z)=\frac{c_{-m}}{(z-z_0)^m}+\frac{c_{-m+1}}{(z-z_0)^{m-1}}+\frac{c_{-m+2}}{(z-z_0)^{m-2}}+\dots + \\[1.5em] +\frac{c_{-1}}{z-z_0}+c_0+c_1(z-z_0)+c_2(z-z_0)^2+\dots
Moltiplicando primo e secondo membro per (z-z0)m risulta (per fare entrare un numero cospicuo di termini viene ridotta la dimensione del font, in caso di difficoltà è sufficiente ingrandire la pagina con la combinazione di tasti Ctrl+ e per riportarlo al 100% con Ctrl-, il riferimento è al browser Firefox):
\scriptsize{(z-z_0)^mf(z)=c_{-m}+c_{-m+1}(z-z_0)+c_{-m+2}(z-z_0)^2+\dots +c_{-1}(z-z_0)^{m-1}+c_0(z-z_0)^m+c_1(z-z_0)^{m+1}+\dots}
Poiché si è interessati al coefficiente c-1 (residuo) allora si può pensare di derivare ambo i membri m-1 volte ottenendo così:
\left | \begin{array}{lllll} \frac{d[(z-z_0)^m f(z)]}{dz}=\scriptsize{c_{-m+1}+2c_{-m+2}(z-z_0)+\dots +(m-1)c_{-1}(z-z_0)^{m-2}+m c_0(z-z_0)^{m-1}+(m+1) c_1(z-z_0)^{m}+\dots} \\ \frac{d^2 [(z-z_0)^m f(z)]}{dz^2}=\scriptsize{2c_{-m+2}+\dots +(m-1)(m-2)c_{-1}(z-z_0)^{m-3}+m(m-1)c_0(z-z_0)^{m-2}+(m+1)mc_1(z-z_0)^{m-1}+\dots} \\ \frac{d^3 [(z-z_0)^m f(z)]}{dz^3}=\scriptsize{\dots +(m-1)(m-2)(m-3)c_{-1}(z-z_0)^{m-4}+m(m-1)(m-2)c_0(z-z_0)^{m-3}+\dots} \\ \vdots \\ \frac{d^{m-1} [(z-z_0)^m f(z)]}{dz^{m-1}}=\scriptsize{\underbrace{(m-1)(m-2)(m-3)\dots 2\space 1}_{(m-1)!} c_{-1}+m(m-1)(m-2)\dots 2\space 1 c_0(z-z_0)+\dots} \end{array} \right.
Riscrivendo solo la derivata di ordine m-1:
\frac{d^{m-1} [(z-z_0)^m f(z)]}{dz^{m-1}}=(m-1)!\space c_{-1}+m(m-1)(m-2)\dots 2\space 1 c_0(z-z_0)+\dots
la quale permette di ricavare il residuo calcolando il limite di z→z0, ovvero:
c_{-1}=\frac{1}{(m-1)!}\lim_{z\to z_0}\frac{d^{m-1}}{dz^{m-1}} [(z-z_0)^m f(z)]
con notazione più semplice è possibile scrivere:
Res.(f,z_0)=\frac{1}{(m-1)!}f^{m-1}(z_0)
Logaritmo nel campo complesso
È noto come dato un numero complesso, la sua forma esponenziale sia possibile scriverla:
z=u+\imath v=\rho e^{\imath\theta}
Il logaritmo di un numero complesso, ricordando anche le proprietà elementari dei logaritmi, può essere scritto come:
\log z=\log(\rho e^{\imath\theta})=\log\rho+\log e^{\imath\theta}
ma la rappresentazione dell’esponenziale non è unica in θ, altrimenti detto scrivere:
e^{\imath\theta}=e^{\imath\theta+2\pi k\imath}
vuol dire scrivere lo stesso numero complesso e pertanto non viene modificato nulla. Allora il logaritmo di un numero complesso può essere riscritto come (ricordando che log e=1):
\log z=\log\rho+\log e^{\imath\theta}=\log\rho+\log e^{\imath\theta+2\pi k\imath}=\log\rho+\imath(\theta+2\pi k)
La rappresentazione del logaritmo di un numero complesso nel piano complesso è immediata; è una linea verticale distante log ρ (quindi a valori positivi) dall’origine. Su questa linea verticale possiamo riportare ad esempio il valore di θ per k=0 per avere un valore del logaritmo complesso log z.
Se per l’argomento di z si sceglie un numero compreso in un assegnato intervallo di ampiezza 2π, come riportato poco sopra per k=0, allora si ha un solo valore e si è isolato un solo argomento del numero complesso z. Generalmente una scelta comune vede −π≤θ=arg(z)<π oppure 0≤θ=arg(z)<2π. In questi casi si parla di valore principale dell’argomento.
Se andiamo oltre il valore principale dell’argomento cioè variamo k, ci si potrà accorgere che il logaritmo del numero complesso presenta sempre la stessa parte reale – sempre log ρ – e ciò che viene modificata è la parte immaginaria generando così numeri complessi che nel piano complesso giacciono su una retta verticale coincidente con log ρ per la parte reale mentre per la parte immaginaria sono tutti punti distanziati di 2π.
Ad esempio dato il numero complesso:
z=1-\imath\sqrt{3}=2e^{-\imath\frac{\pi}{3}+2\pi k\imath}
Il logaritmo di questo numero complesso è:
\log z=\log 2+\imath(-\frac{\pi}{3}+2\pi k)
che avrà come risultato un numero complesso con parte reale pari sempre a log 2 e parte immaginaria -π/3 se ci si limita al valore principale, ovvero infiniti valori distanziati tra di loro di 2π sulla retta verticale di valore log 2 al variare di k. In definitiva ogni numero complesso non nullo presenta infiniti logaritmi.
Teorema dell’indicatore logaritmico

Una conseguenza del teorema dei residui è il teorema dell’indicatore logaritmico o principio dell’argomento per il quale:
Ipotesi: se Γ è una curva chiusa nel dominio \wp del piano s e f(z) è una funzione analitica in \wp, ad eccezione di un numero finito di poli α di ordine p e zeri β di ordine n, e se f(z)\not=0 \forall s \in \Complex ;
Tesi: allora risulta
\frac{1}{2\pi\imath}\oint_{\Gamma}{\frac{f^{'}(z)}{f(z)}dz}=n-p
ovvero la differenza d’ordine tra uno zero e un polo e laddove con f‘(z) si è indicata la derivata prima della f(z).
Dimostrazione: se la funzione f(z) ha un polo in α di ordine p allora dai concetti di singolarità riportati in precedenza è possibile esprimerla come:
f(z)=\frac{F(z)}{(z-\alpha)^p}
con F(z) olomorfa, quindi F(z) \in H(\wp) \space \text{e} \space F(\alpha)\not=0.
Si consideri il logaritmo di ambo i membri della funzione precedente, allora ricordando le proprietà elementari dei logaritmi si può scrivere come:
\log[f(z)]=\log\left[\frac{F(z)}{(z-\alpha)^p}\right]=\log F(z)-\log(z-\alpha)^p
ovvero:
\log[f(z)]=\log F(z)-p\log(z-\alpha)
Derivando ambi i membri dell’ultima uguaglianza si ottiene per il primo membro:
\frac{d}{dz}\log[f(z)]=\frac{f^{'}(z)}{f(z)}
mentre per il secondo membro:
\frac{d}{dz}\log [F(z)]-p\frac{d}{dz}\log(z-\alpha)=\frac{F^{'}(z)}{F(z)}-p\frac{1}{(z-\alpha)}
Per l’uguaglianza tra primo e secondo membro il risultato vede:
\frac{f^{'}(z)}{f(z)}=\frac{F^{'}(z)}{F(z)}-p\frac{1}{(z-\alpha)}\kern{1cm}Eq.1
Costruita una circonferenza comunque piccola intorno ad α e β, per il teorema di Cauchy precedentemente dimostrato è possibile scrivere:
\frac{1}{2\pi\imath}\oint_{\Gamma}{\frac{f^{'}(\xi)}{f(\xi)}d\xi}=\frac{1}{2\pi\imath}\oint_{\Gamma_1}{\frac{f^{'}(\xi)}{f(\xi)}d\xi}+\frac{1}{2\pi\imath}\oint_{\Gamma_2}{\frac{f^{'}(\xi)}{f(\xi)}d\xi}\kern{1cm}Eq.2
Ma Eq.1 è stata ottenuta ipotizzando che α sia un polo in Γ1 pertanto il primo addendo a secondo membro di Eq.2 è possibile scriverlo, considerando Eq.1:
\frac{1}{2\pi\imath}\oint_{\Gamma_1}{\frac{f^{'}(\xi)}{f(\xi)}d\xi}=\frac{1}{2\pi\imath}\oint_{\Gamma_1}{\frac{F^{'}(\xi)}{F(\xi)}d\xi}-\frac{p}{2\pi\imath}\oint_{\Gamma_1}{\frac{1}{(\xi-\alpha)}d\xi}
con ξ variabile di integrazione. Ora occorre osservare che:
\frac{1}{2\pi\imath}\oint_{\Gamma_1}{\frac{F^{'}(\xi)}{F(\xi)}d\xi}=0
questo perché si è ipotizzato che la funzione F(z) è analitica in tutto \wp e inoltre che la F(z)≠0 su Γ. Poiché la derivata di una funzione analitica è ancora una funzione analitica e il rapporto tra due funzioni analitiche da come risultato ancora una funzione analitica allora, per il teorema di Cauchy, l’integrale di una funzione analitica esteso ad una curva regolare e chiusa è nullo. Per il secondo addendo ricordando che \xi\isin\Complex allora è possibile scrivere \xi(t)=\alpha+re^{\imath t} e per il quale il differenziale è pari a d\xi=\imath r e^{\imath t}dt, espressioni che sostituite nel secondo addendo forniscono:
-\frac{p}{2\pi\imath}\int_0^{2\pi}\frac{1}{\cancel{\alpha}+re^{\imath t}-\cancel{\alpha}}\imath \space re^{\imath t}\space dt=-\frac{p}{2\pi\cancel{\imath}}\int_0^{2\pi}\frac{1}{\cancel{re^{\imath t}}}\cancel{\imath} \space \cancel{re^{\imath t}}\space dt=\\[1.5em]=-\frac{p}{2\pi}\int_0^{2\pi}dt=-\frac{p}{\cancel{2\pi}}\space \cancel{2\pi}=-p
In definitiva se la funzione in α presenta un polo la Eq.2 si può riscrivere come:
\frac{1}{2\pi\imath}\oint_{\Gamma}{\frac{f^{'}(\xi)}{f(\xi)}d\xi}=-p+\frac{1}{2\pi\imath}\oint_{\Gamma_2}{\frac{f^{'}(\xi)}{f(\xi)}d\xi}
Rimane da valutare l’integrale su Γ2. Per ipotesi la funzione in β ha uno zero di ordine n quindi è possibile riscriverla come:
f(z)=(z-\beta)^n G(z) \space \text{ laddove } G(z)|_{z=\beta}\not=0
Effettuando il logaritmo a primo e secondo membro e per le proprietà elementari degli stessi è possibile scrivere:
\log f(z)=\log[(z-\beta)^n G(z)]=\log(z-\beta)^n+\log G(z)
ovvero a:
\log f(z)=n\log(z-\beta)+\log G(z)
nella quale derivando ambo i membri risulta per il primo membro:
\frac{d}{dz}\log[f(z)]=\frac{f^{'}(z)}{f(z)}
mentre per il secondo membro:
n\frac{d}{dz}\log(z-\beta)+\frac{d}{dz}\log g(z)=\frac{n}{z-\beta}+\frac{G^{'}(z)}{G(z)}
Per l’uguaglianza tra primo e secondo membro è possibile così scrivere:
\frac{f^{'}(z)}{f(z)}=\frac{n}{z-\beta}+\frac{G^{'}(z)}{G(z)}
la quale integrata membro a membro su Γ2 porta a:
\frac{1}{2\pi\imath}\oint_{\Gamma_2}{\frac{f^{'}(\xi)}{f(\xi)}d\xi}=\frac{1}{2\pi\imath}\oint_{\Gamma_2}{\frac{G^{'}(\xi)}{G(\xi)}d\xi}+\frac{1}{2\pi\imath}\oint_{\Gamma_2}{\frac{n}{(\xi-\beta)}d\xi}
ragionando allo stesso modo visto per il polo risulta:
\frac{1}{2\pi\imath}\oint_{\Gamma_2}{\frac{G^{'}(\xi)}{G(\xi)}d\xi}=0
Per il secondo addendo a secondo membro si può invece scrivere, con analogo procedimento visto per il polo e ricordando che \xi(t)=\beta+re^{\imath t} il cui differenziale è pari a d\xi=\imath r e^{\imath t}dt:
\frac{1}{2\pi\imath}\oint_{\Gamma_2}{\frac{n}{(\xi-\beta)}d\xi}=\frac{n}{2\pi}\int_0^{2\pi}dt=n
In definitiva, per i risultati fin qui dimostrati, la Eq.2 è possibile riscriverla come:
\frac{1}{2\pi\imath}\oint_{\Gamma}{\frac{f^{'}(\xi)}{f(\xi)}d\xi}=\frac{1}{2\pi\imath}\oint_{\Gamma_1}{\frac{f^{'}(\xi)}{f(\xi)}d\xi}+\frac{1}{2\pi\imath}\oint_{\Gamma_2}{\frac{f^{'}(\xi)}{f(\xi)}d\xi}=-p+n=n-p
Che è esattamente ciò che si voleva dimostrare. Va dase che nel caso di più poli e più zeri sarà possibile generalizzare la discussione nel modo che segue. Se:
\sum_{j=1}^{l} p_j=P \text{ e se } \sum_{i=1}^{k} n_j=N
allora generalizzando la Eq.2 è possibile scrivere:
\frac{1}{2\pi\imath}\oint_{\Gamma}{\frac{f^{'}(\xi)}{f(\xi)}d\xi}=\frac{1}{2\pi\imath}\sum_{j=1}^{l}\oint_{\Gamma_j}{\frac{f^{'}(\xi)}{f(\xi)}d\xi}+\frac{1}{2\pi\imath}\sum_{i=1}^{k}\oint_{C_i}{\frac{f^{'}(\xi)}{f(\xi)}d\xi}=\\[1.5em]=-\sum_{j=1}^{l} p_j+\sum_{i=1}^{k} n_j=N-P\\[1.5em]c.v.d.
Conclusioni
Arrivati a questo punto come legare i risultati ottenuti con il criterio di Nyquist? Prima di tutto la funzione integranda utilizzata nell’integrale del teorema dell’argomento viene definita come derivata logaritmica, infatti è immediato verificare che:
\frac{d}{d\xi}\ln f(\xi)=\frac{f^{'}(\xi)}{f(\xi)}
una definizione largamente utilizzata in prodotti e produttorie a causa delle proprietà dei logaritmi di trasformare prodotti in somme. Se nella precedente provassimo ad integrare in maniera indefinita primo e secondo membro ne risulterebbe:
\int{\frac{f^{'}(\xi)}{f(\xi)}d\xi}=\log f(z)
Se ora poniamo w=f(z) allora ecco che w altro non è che un numero complesso al variare di z potendosi così scrivere la precedente come, ricordando il logaritmo complesso richiamato poco sopra:
\int{\frac{f^{'}(\xi)}{f(\xi)}d\xi}=\log w=\log |w|+\imath\phase{w}
Il riportato integrale esteso ad un cammino semplice chiuso può essere riscritto come:
\oint{\frac{f^{'}(\xi)}{f(\xi)}d\xi}=\log |w|+\imath\phase{w}
nel quale è evidente come |f(z)| (ovvero w) dopo un giro completo assuma di nuovo lo stesso valore, cosa non necessariamente vera per l’argomento il quale dopo un giro sarà generalmente mutato. Allora dividendo primo e secondo membro per 2πι e indicando con ΔΓ(∠f(z)) la variazione dell’argomento della f(z) lungo la curva Γ, il precedente integrale si può riscrivere come:
\frac{1}{2\pi\imath}\oint{\frac{f^{'}(\xi)}{f(\xi)}d\xi}=\frac{1}{2\pi}\Delta_\Gamma(\phase{f(z)})
laddove il termine:
\frac{\Delta_\Gamma(\phase{f(z)})}{2\pi}
è esattamente N il numero di giri in senso orario (il senso che nell’analisi condotta indica angoli positivi) che la f(z) fa attorno all’origine al variare dei punti z∈Γ.
Ma per il teorema dell’argomento l’integrale a primo membro è uguale a n-p pertanto si può scrivere:
\frac{\Delta_\Gamma(\phase{f(z)})}{2\pi}=N=n-p
cioè il risultato che si voleva dimostrare e sul quale poggia in criterio di Nyquist.
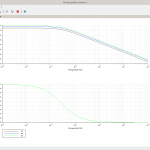
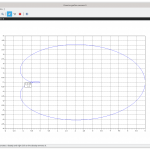
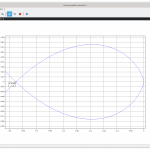
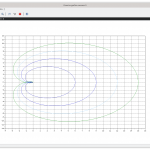
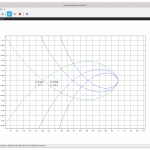


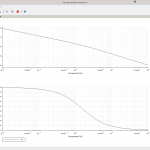

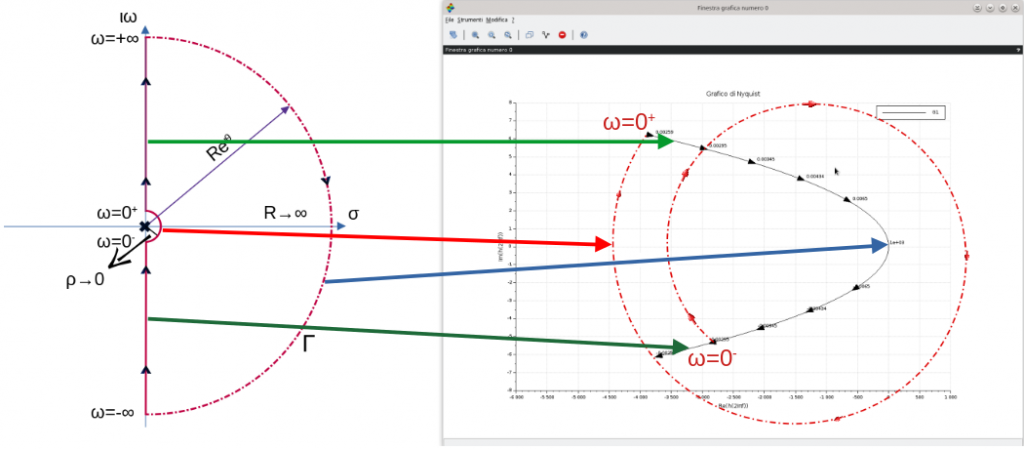
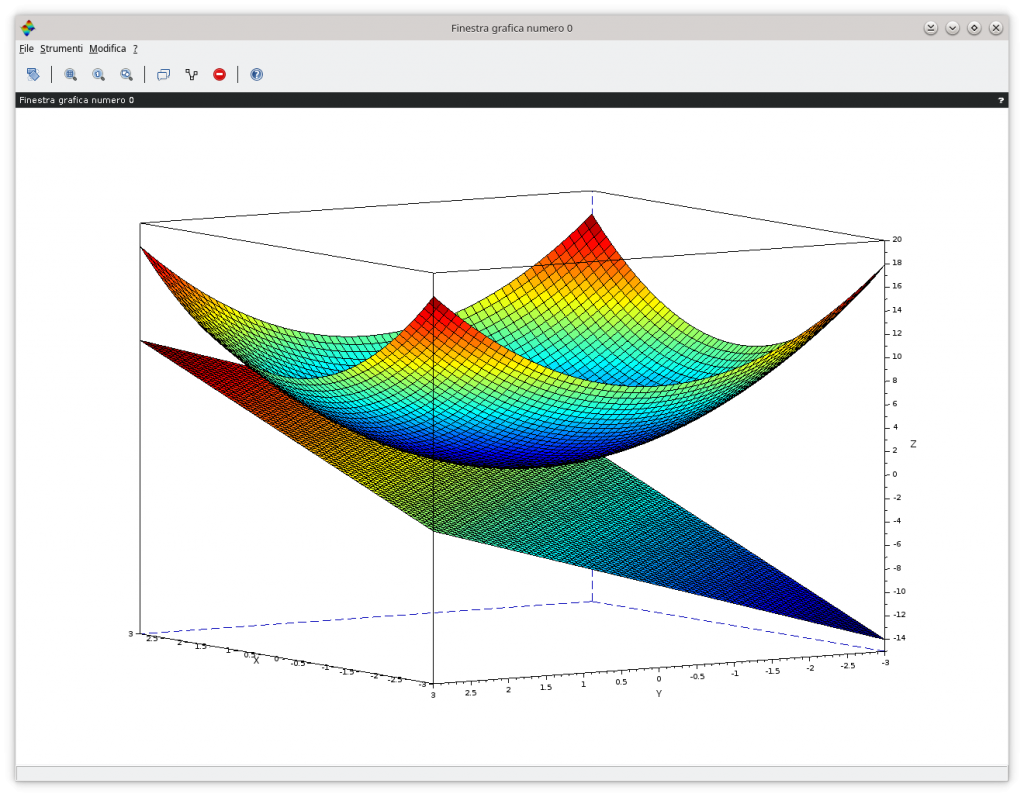
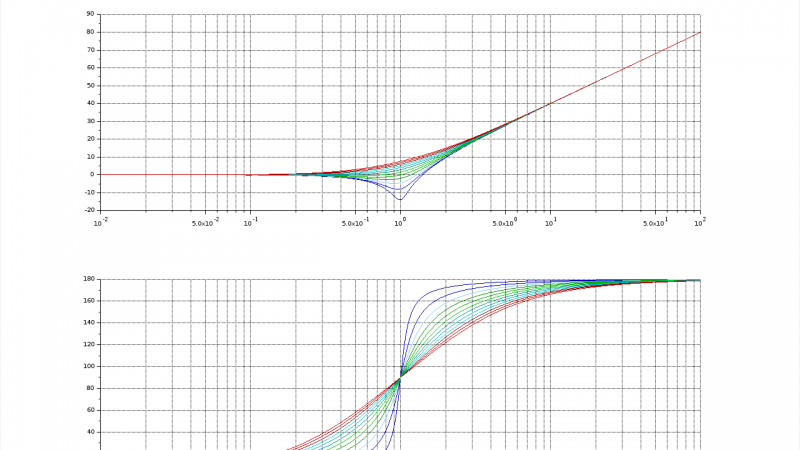
Un pensiero su “Criterio di stabilità di Nyquist”