Triodo: circuito equivalente

Prima di tutto: perché trattare il circuito equivalente di un dispositivo avente un’origine risalente agli inizi del ‘900? Semplicemente perché in un futuro articolo verrà trattato l’effetto (e il teorema di) Miller definiti alla fine degli anni ’10 del precedente millennio …e in quel contesto storico si avevano a disposizione solo tubi a vuoto (il concetto di effetto di campo, precursore dei moderni JFET e MOSFET, si concretizzò solo nel 1925) e in particolare i triodi sul quale un tale di nome Miller lavorò per risolvere un noto problema in frequenza a cui venne poi dato il nome di effetto (e teorema di) Miller.

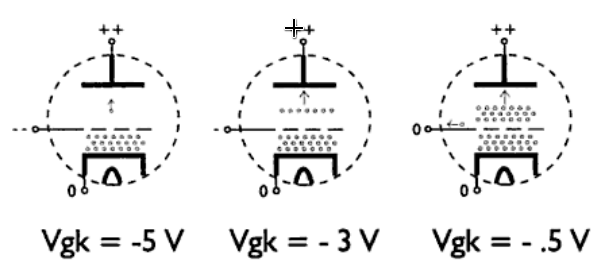
La struttura costruttiva di un triodo vede, fondamentalmente, tre elementi disposti coassialmente: nella parte più interna è presente il catodo, elemento metallico riscaldato direttamente o indirettamente tramite un filamento con lo scopo di realizzare un emettitore di elettroni per effetto termoelettrico.

Attorno al catodo, opportunamente distanziato e isolato, si trova un avvolgimento metallico detto griglia.

A racchiudere griglia e catodo – ed elettricamente isolati da essi – si trova una sorta di tubo metallico detto anodo o placca. Il tutto, occorre ricordare, è racchiuso all’interno di una ampolla di vetro dove viene realizzato il vuoto al fine di evitare l’interazione degli elettroni con residui gassosi. La figura in basso riporta i suddetti elementi.

Per quanto ne attiene il funzionamento di seguito è riportato solo in forma intuitiva; la trattazione analitica – non proprio banale – verrà aggiunta quanto prima a questa trattazione al fine di completarla adeguatamente. Quando l’elemento riscaldante (il filamento) viene alimentato la temperatura del catodo viene portata a valori intorno ai 700°C. In queste condizioni, causa effetto termoelettrico, vengono emessi elettroni dalla superficie metallica del catodo. Se griglia e anodo non sono connessi a nulla gli elettroni emessi vanno a realizzare una sorta di “nuvola elettronica” di carica spaziale negativa intorno al catodo. Non si disperdono nello spazio circostante poiché si forma un equilibrio dipendente dalla temperatura raggiunta dal catodo. Equilibrio che vede una emissione continua di elettroni ad opera del catodo e una ricaduta su di esso per effetto delle forze di Coulomb che agiscono sugli elettroni e dovute alle cariche positive presenti sul catodo a seguito della cessione degli elettroni. In queste condizioni qualsiasi potenziale applicato alla griglia e/o all’anodo perturberà il suddetto equilibrio. È possibile distinguere diversi casi.

Come primo si ipotizzi l’assenza della griglia. Se il potenziale dell’anodo (placca) è più negativo rispetto al catodo la “nuvola di elettroni” tende ad esser schiacciata – per effetto repulsivo del potenziale di placca – verso il catodo che pertanto vedrà aumentata la densità di elettroni attorno ad esso. In queste condizioni la corrente circolante è pari a 0.

Sempre ipotizzando l’assenza dell’elettrodo di griglia, se il potenziale dell’anodo è portato ad un valore superiore al catodo gli elettroni presenti nella “nuvola di carica spaziale” verranno attratti verso la placca originando così una corrente anodica (o di placca). Tale valore di corrente è tanto maggiore quanto più positivo è il potenziale dell’anodo rispetto al catodo con il limite superiore (saturazione) indotto dalla quantità di elettroni che il catodo riesce ad emettere, funzioni a sua volta del tipo di materiale utilizzato per il catodo e della temperatura raggiunta. Quanto riportato è il tipico funzionamento di un diodo a vuoto la cui caratteristica corrente anodica vs tensione anodica (fissati che siano gli altri parametri, e.g. temperatura e materiale costituente il catodo) è visibile nel datasheet in basso per il diodo 6W4GT.

6w4gt

Poiché l’obiettivo è il circuito equivalente del triodo è possibile completare il discorso facendo intervenire la griglia. Il potenziale della griglia influisce sul comportamento del triodo ovvero sul passaggio degli elettroni dal catodo all’anodo. Un potenziale più negativo della griglia rispetto al catodo ostacola il passaggio degli elettroni verso l’anodo con il risultato di vedere una corrente anodica minore rispetto al caso in cui la griglia risulti assente o avesse una tensione meno negativa.

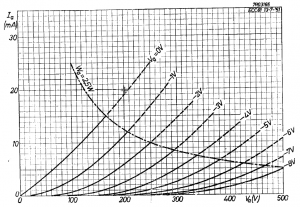
Per ogni fissato valore della tensione di griglia è allora possibile variare la tensione anodica (compatibilmente con il massimo valore accettato dal tubo) e misurarne la corrente di placca. Una siffatta procedura permette di disegnare una famiglia di curve che nel loro complesso determinano la caratteristica di uscita di un triodo che vede sulle ordinate la corrente anodica, sulle ascisse la tensione anodica e come parametro la tensione di griglia. Si vede chiaramente come all’aumentare del potenziale negativo della griglia la corrente anodica vada via via riducendosi fino ad azzerarsi (interdizione) in funzione anche della tensione anodica. Un siffatto andamento, oltre a poter essere evidenziato con una semplice prova di laboratorio, presenta una giustificazione analitica non semplice che quanto prima verrà aggiunta a questa trattazione al fine di completarla adeguatamente. La famiglia di curve riportata è tipica del doppio triodo ECC81 il cui datasheet è visibile in basso.

ECC81

In definitiva il controllo della corrente anodica è ottenuto per mezzo della tensione di griglia e siccome il suo potenziale è più o meno negativo rispetto al catodo si avrà una continua repulsione di elettroni che potrebbe indurre a pensare ad una corrente pari a 0. In realtà non è così il valore della corrente di griglia solitamente si aggira intorno alle decine di μA a salire. Ad esempio è di circa 50μA nel caso del triodo EC86 come da datasheet.

EC86

Per quanto fin qui detto è possibile riportare una descrizione formale del comportamento elettrico del triodo osservando come le variabili indipendenti risultino la tensione anodica e la tensione di griglia mentre le variabili dipendenti le correnti (anodica e di griglia). Esplicitando in forma analitica le suddette relazioni è possibile scrivere:

\left \{  \begin{array}{ll} i_A=i_A(v_A, v_G)\\i_G \simeq 0 \end{array} \right.

È importante osservare che una siffatta notazione prevede implicitamente la presenza di una componente continua utilizzata per indicare il punto di funzionamento a riposo del triodo pertanto, avendo due componenti di corrente (anodica e di griglia) e due componenti di tensione (anodica e di griglia), si può scrivere:

\left \{ \begin{array}{llll} v_A=V_A+v_a\\v_G=V_G+v_g\\i_A=I_A+i_a\\i_G=I_G+i_g \end{array} \right.

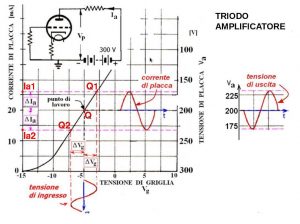Laddove Y_X indica la componente continua del punto di funzionamento a riposo (o punto quiescente Q) e y_x la componente del segnale (e.g. un segnale sinusoidale). La figura a lato illustra bene la dinamica sulla curva I_a=f(V_g) fissato (parametro) il valore della tensione anodica V_a. Applicando un segnale in ingresso il punto di funzionamento del triodo si sposterà seguendo l’andamento del segnale. Durante la semionda positiva si porterà fino al punto Q1 corrispondente alla corrente anodica Ia1. Quando il segnale di ingresso assumerà valore negativo il punto si sposterà su Q2 corrispondente alla corrente anodica Ia2. Quando il punto di funzionamento è Q1 la corrente anodica risulterà:

i_A=f(V_Q+\Delta V_g)

Come noto dall’analisi matematica, una funzione – sotto determinate condizioni che in questa sede non interessano – può essere rappresentata intorno ad un punto attraverso uno sviluppo in serie di Taylor la cui formula compatta, per funzioni di due variabili, assume la forma:

f(x_1,x_2)=\sum_{n1=0}^{\infty} \sum_{n2=0}^{\infty} \frac{\partial^{n1}}{\partial x_1^{n1}} \frac{\partial^{n2}}{\partial x_2^{n2}} \frac{f(a_1,a_2)}{n_1!n_2!} (x_1-a_1)^{n1} (x_2-a_2)^{n2}

Perché per funzioni di due variabili? Perché la corrente anodica è funzione di due variabili indipendenti: la tensione anodica e la tensione di griglia, come già riportato i_A=i_A(v_A, v_G). Espandendo la corrente anodica in serie di Taylor attorno al punto Q il suo sviluppo risulterà (applicando la formula precedente):

\left. i_A=i_A|_{Q}+\frac{\partial i_A}{\partial v_A}\bigg|_{Q}v_a+\frac{\partial i_A}{\partial v_G}\right|_{\substack{Q}}v_g+ \\[1.5ex] +\frac{1}{2!}\frac{\partial ^2 i_A}{\partial ^2 v_A}\bigg|_{Q}v_a^2+\frac{1}{2!}\frac{\partial ^2 i_A}{\partial ^2 v_G}\bigg|_{Q}v_g^2+\frac{\partial ^2 i_A}{\partial v_A \partial v_G}\bigg|_{Q}v_av_g+ \\[1.5ex] +\:Termini\;di\;ordine\;superiore\;al\;secondo

Al ridursi del valore \Delta V_g il triodo si troverà a lavorare sempre più in un intorno via via più piccolo del punto Q il che vuol dire che l’escursione intorno al punto di riposo potrà essere considerata lineare e con essa la corrente anodica. Ciò permette di poter troncare l’espressione dell’espansione di Taylor al primo termine trascurando tutti i termini di ordine 2 e superiori ottenendo il polinomio di Taylor corrispondente:

\left. i_A \simeq i_A|_{Q}+\frac{\partial i_A}{\partial v_A}\bigg|_{Q}v_a+\frac{\partial i_A}{\partial v_G}\right|_{\substack{Q}}v_g

ed essendo i_A=I_A+i_a si può scrivere:

\left. I_A+i_a=i_A|_{Q}+\frac{\partial i_A}{\partial v_A}\bigg|_{Q}v_a+\frac{\partial i_A}{\partial v_G}\right|_{\substack{Q}}v_g

ma il valore i_A calcolato nel punto Q è I_A pertanto:

\left. i_a=\frac{\partial i_A}{\partial v_A}\bigg|_{Q}v_a+\frac{\partial i_A}{\partial v_G}\right|_{\substack{Q}}v_g

risultato che fornisce una relazione lineare tra le componenti di segnale e dal quale è possibile estrapolarne il modello per piccoli segnali o modello incrementale. Riscrivendo il risultato nel modo seguente:

i_a=g_pv_a+g_mv_g

avendo posto:

\left \{ \begin{array}{ll} g_p=\frac{\partial i_A}{\partial v_A}\bigg|_{Q} \Rightarrow\;Conduttanza\;incrementale\;d'uscita\\[3ex]  g_m=\frac{\partial i_A}{\partial v_G}\bigg|_{Q} \Rightarrow\;Trasconduttanza\; incrementale \end{array} \right.

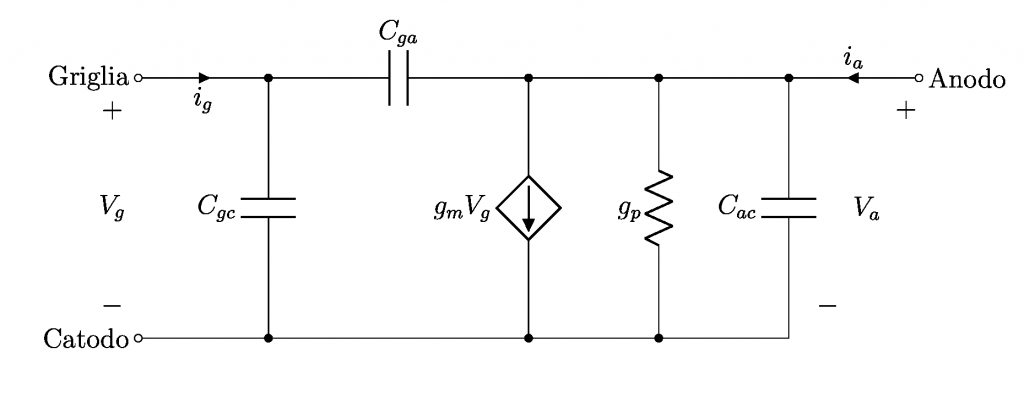
che porta al circuito equivalente per piccoli segnali (o modello incrementale) del triodo:

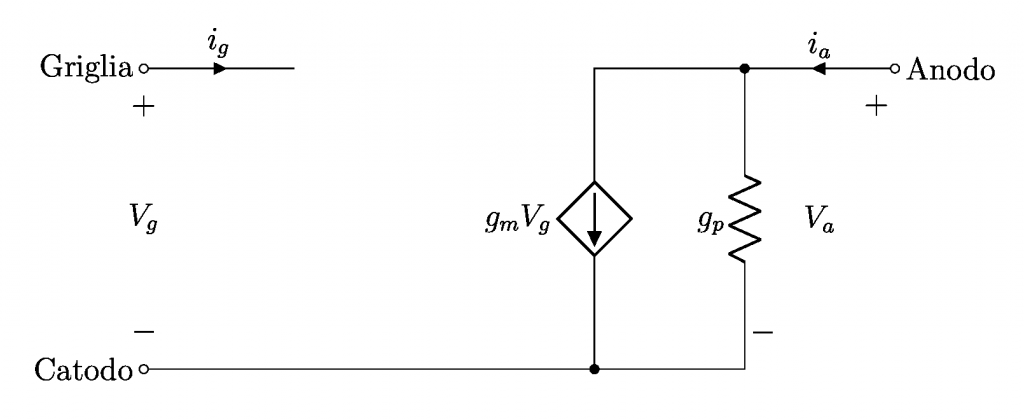
Nel funzionamento del triodo (ma un medesimo discorso può essere traslato per il diodo a vuoto, e viceversa) non è stata presa in considerazione la frequenza di funzionamento. Infatti, se il modello per piccoli segnali della figura precedente può ritenersi valido a basse frequenze, inizia a cadere in difetto allorquando la frequenza del segnale sale sull’ordine dei 10^7\;Hz e oltre. In queste condizioni di funzionamento intervengono un numero di effetti non più trascurabili, ad esempio:

• Il periodo del segnale, all’aumentare della frequenza, si avvicina sempre più al tempo di transito degli elettroni;
• All’aumentare della frequenza si fanno sempre più consistenti le correnti di spostamento tali da non poterle più trascurare rispetto alle correnti di conduzione;

Queste parti verranno adeguatamente spiegate quanto prima e aggiunte a questa trattazione al fine di completarla, per ora ci si accontenta della loro definizione. Le correnti di spostamento possono essere rappresentate tramite delle capacità tra elettrodi (capacità interelettrodiche), una per ogni coppia di elettrodi risultando il circuito equivalente: