Esempio 1cc: Serie-Parallelo di resistenze

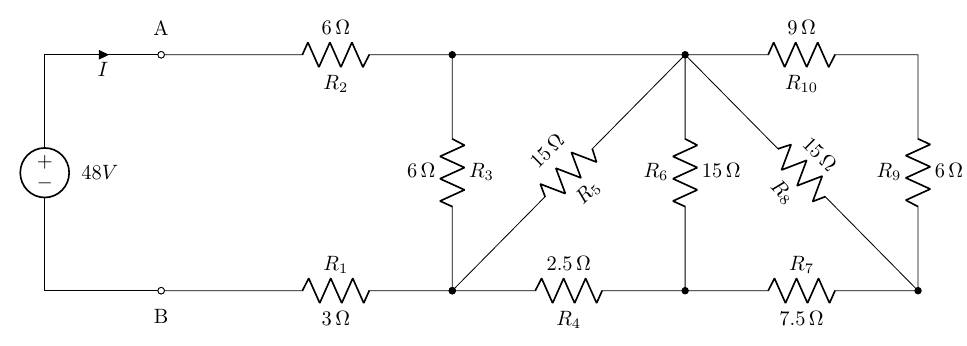
Del circuito dell’immagine di apertura si calcoli la corrente erogata dal generatore ideale di tensione.

Prima di iniziare la procedura che porterà alla soluzione, si vuole ricordare che del circuito visibile in alto è riportato il sorgente $TeX-LaTeX$ al seguente indirizzo. Tutte le immagini che seguiranno lo svolgimento dell’esempio altro non saranno altro che semplici modifiche al suddetto sorgente per adeguare di volta in volta lo schema equivalente.

Al fine di calcolare la corrente erogata dal generatore ideale di tensione occorre valutare il valore della resistenza equivalente tra i punti A e B. Osservando il circuito si può notare come le due resistenze $R_9, R_{10}$ siano in serie pertanto si possono semplificare con un un’unica resistenza $R_{S1}$ pari alla somma delle due:

$R_{S1}=R_9+R_{10}=9 + 6=15\Omega$

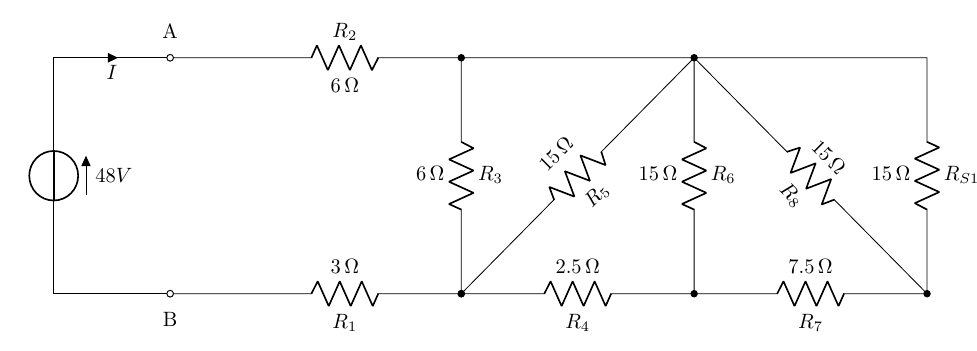
e il nuovo circuito diventa:

Da questo circuito è facile notare come le due resistenze $R_{S1}-R_8$ siano tra di loro in parallelo. Ricordando il caso particolare di due resistenze in parallelo, è possibile sostituire le due resistenze con una di valore:

$R_{P1}=\frac{R_8\times R_{S1}}{R_8+R_{S1}}=\frac{15\times 15}{15+15}=7,5\Omega$

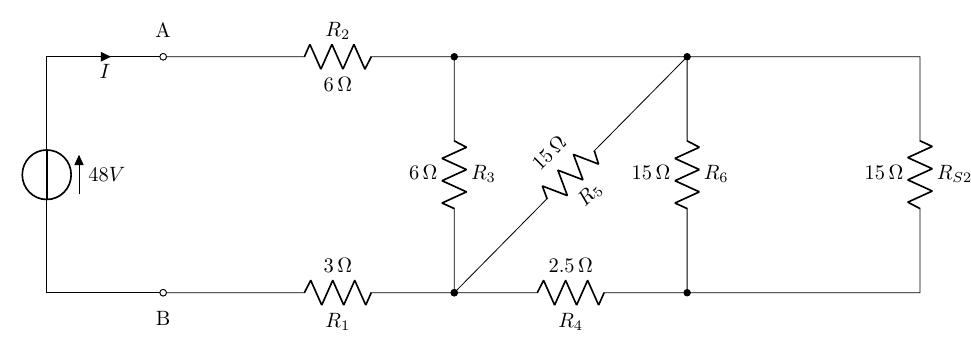
portando così il circuito ad essere:

Ma la resistenza $R_{P1}$ è in serie con $R_7$ pertanto, ancora una volta, si possono sostituire con un unico valore di resistenza:

$R_{S2}=R_{P1}+R_7=7,5+7,5=15\Omega$

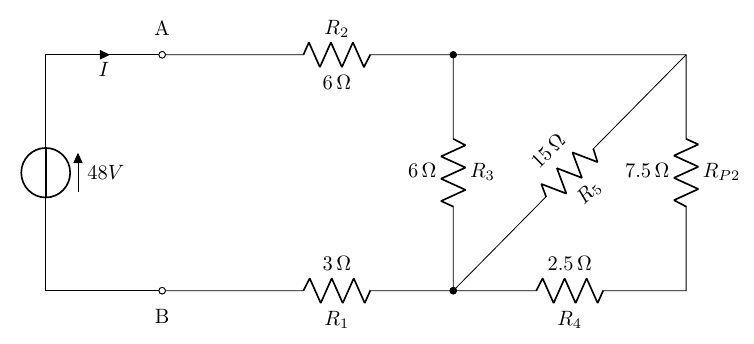
Si ripete la situazione del passo precedente: la resistenza $R_{S2}$ è in parallelo con la resistenza $R_6$ , pertanto le si possono sostituire con una sola resistenza di valore pari a:

$R_{P2}=\frac{R_{S2}\times R_6}{R_{S2} + R_6}=\frac{15\times 15}{15+15}=7,5\Omega$

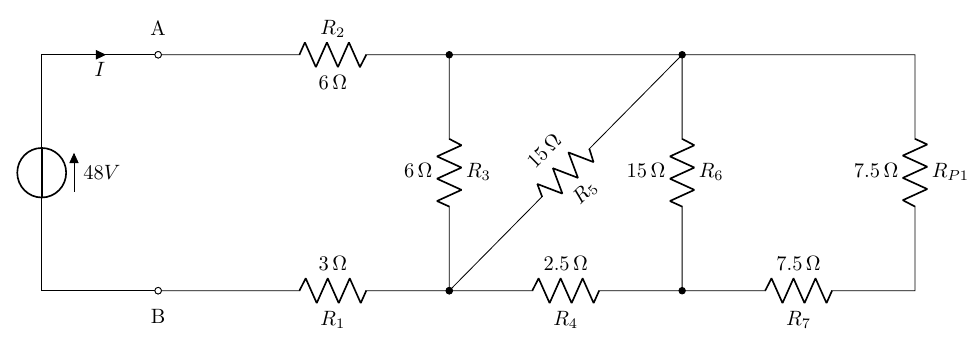
Il nuovo circuito diventa:

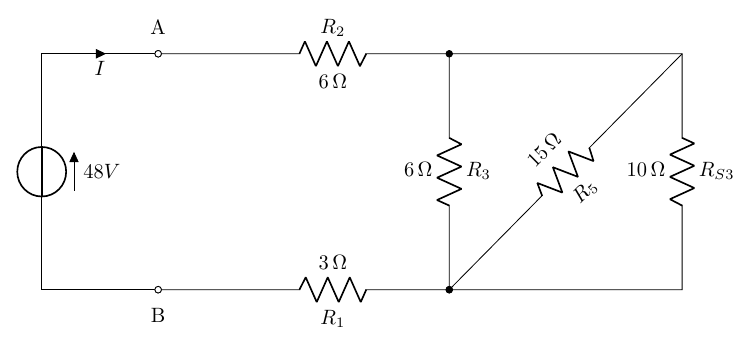
Di nuovo $R_{P2}$ e $R_4$ in serie che originano una sola resistenza di valore:

$R_{S3}=R_{P2}+R_4=7,5+2,5=10\Omega$

e quindi il nuovo circuito equivalente:

il quale è caratterizzato da 3 resistenze in parallelo il cui valore equivalente – applicando la formula generale per 3 o più elementi in parallelo – è pari a:

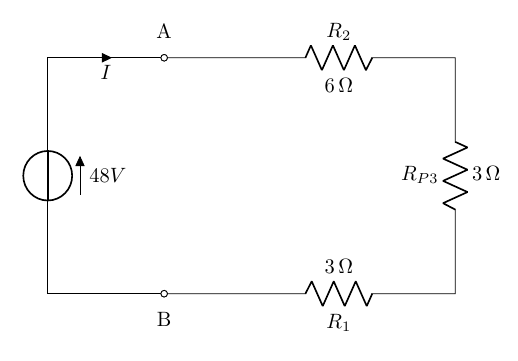
$R_{P3}=\frac{1}{\frac{1}{R_{S3}}+\frac{1}{R_5}+\frac{1}{R_3}}=\frac{1}{\frac{1}{10}+\frac{1}{15}+\frac{1}{6}}=3\Omega$

che porta al circuito equivalente: