Introduzione

Nel seguito presenterò, in maniera abbastanza dettagliata, la progettazione di un off-line DCM flyback converter idoneo al monitor “home made” che ho realizzato un po’ di tempo fa e questo al fine di completarlo, renderlo autonomo e trasportabile per essere utilizzato in ogni contesto.

Il design – leggasi progettazione – di un alimentatore a commutazione noti con la sigla SMPS, acronimo di Switched Mode Power Supply, è intrinsecamente un lavoro che richiede un minimo di tempo, alcuni compromessi e un certo numero di prove/iterazioni essendovi in gioco un numero non indifferente di variabili.

La procedura di progettazione descritta passo passo (suddivisa in diverse parti) potrà aiutare chiunque abbia un minimo di conoscenze nel settore a rendere più comprensivi i passaggi dietro la progettazione di un SMPS. Farò ampio uso della teoria alla base degli SMPS con tutte le equazioni necessarie – dimostrate di volta in volta – e coadiuvato nei risultati teorici dal simulatore della Analog Devices LTSpice, perfettamente funzionante in ambiente GNU/Linux utilizzando WINE. Infine, ogni volta che si hanno un numero di elementi sufficienti verrà realizzato un prototipo in pratica partendo dal più rudimentale fino ad arrivare al progetto finale su PCB da inserire nel retro del suddetto monitor.

La topologia Flyback è la più utilizzata per applicazioni in bassa potenza – in genere dall’ordine del watt fino a circa 100W seppur con qualche accorgimento per aumentarne il rendimento – e questo in tutti quei casi nei quali l’uscita deve essere isolata galvanicamente dall’ingresso. È la più utilizzata per applicazioni consumer e.g. decoder esterni, caricabatterie per cellulari, alimentatori interni nei monitor ecc. Infatti le sue migliori caratteristiche vedono un basso costo a parità di potenza rispetto ad altre topologie circuitali, una maggiore semplicità, la relativa facilità di implementazione e, se tutto è realizzato al meglio, anche una notevole affidabilità.

Per basse correnti – orientativamente intorno a qualche ampere – e livelli di potenza inferiori a 50 W, la modalità operativa preferita è solitamente la DCM (Discontinuous-Conduction Mode) e questo grazie alla maggiore facilità realizzativa del loop di controllo e alle minori perdite – in proporzione per questi livelli di potenza – rispetto alle altre topologie. Si può stilare un elenco di pro e contro della modalità di funzionamento DCM che si comprenderà meglio nel prosieguo e negli appuntamenti successivi:

• Valore induttanza primaria minore della modalità CCM;
• “Trasformatore” di più piccole dimensioni;
• Nessuno zero nel semipiano destro nella funzione di trasferimento del sistema di controllo.

Ma non vanno dimenticati gli svantaggi al fine di capire quando un flyback DCM può risultare non idoneo ad una data applicazione:

• Corrente di picco primaria e secondaria, elevata;
• Corrente di picco sul ponte/diodi raddrizzatori elevata;
• Necessaria una maggiore capacità di ingresso e di uscita con conseguente aumento delle dimensioni fisiche;
• Variazione del duty-cycle superiore alla modalità CCM.

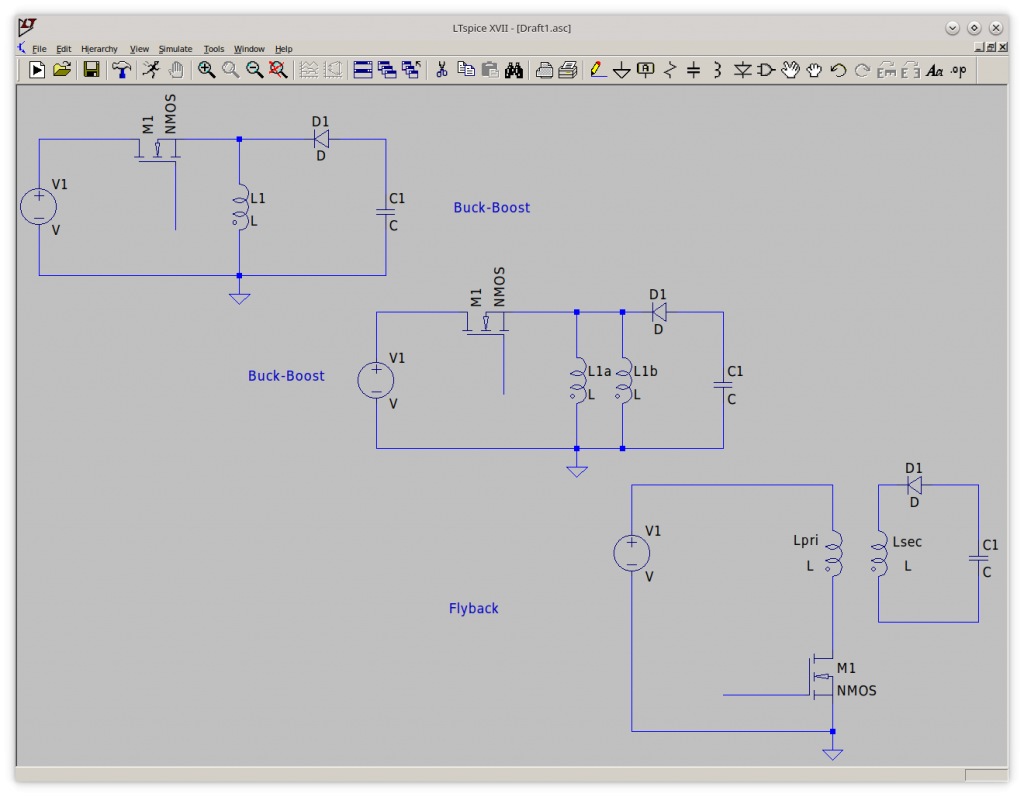
Dal punto di vista pratico il flyback è possibile vederlo come un buck-boost converter di tipo isolato, dove al posto dell’induttanza “trasversa” viene inserito un induttore mutuamente accoppiato (comunemente, ed erroneamente, chiamato “trasformatore”) che garantisce l’isolamento galvanico tra il circuito primario e secondario e il cui schema di principio (schema ideale) è rappresentato nella “evoluzione” della figura che segue.

Il motivo per cui il MOSFET è stato spostato – rispetto alla topologia buck-boost – dalla “parte opposta” dell’induttanza, è dovuto al fatto che la differenza di tensione che lo attiva è la differenza tra i potenziali dei terminali di Gate e Source. Ciò significa che se il terminale di source non è vincolato ad un potenziale fisso, cioè a massa o sulla tensione di alimentazione – rispettivamente per un NMOS e un PMOS – diventa molto più complicato pilotarlo poiché un terminale è flottante (il source) e l’altro (il gate) dovrà adeguarsi di volta in volta al fine di permetterne il corretto pilotaggio.

I parametri del progetto

L’obiettivo è la realizzazione di un flyback DCM necessario ad alimentare il monitor “home made” che si può vedere e leggere nell’articolo Costruire un monitor dallo schermo di un portatile dismesso. Il punto di partenza vede l’impostazione di alcune grandezze note e dalle quali iniziare la fase di progettazione. Valori come V_Im, V_IM, f_S, η, V_O, I_OM sono necessari per iniziare la progettazione. La tensione di ingresso è legata al valore della tensione di rete dei sistemi elettrici pubblici a bassa tensione perché è ad essa che il convertitore dovrà essere collegato. Il valore, come da norma CEI 8-6 riportata in basso, è fissato a 230V ±10% identificando così un possibile range di valori ammissibili (come da tolleranza) compresi tra 207V e 253V.

---

CEI_8-6_1998-04_V1_2005-01_Tensioni_nominali_dei_sistemi_elettrici_di_distribuzione_pubblica_a_bassa_tensione

---

 

In prima approssimazione si ipotizza – come approccio alla progettazione, ipotesi che verrà rimossa in un secondo momento – di partire da una condizione esemplificativa; tensione di linea “fissa” a 230V alternati il che implica, ipotizzando che non ci sia alcuna caduta di tensione tra filtri di ingresso e raddrizzatore, un livello di tensione continua sul futuro condensatore di livellamento pari a 230*1,41=325V. In tali condizioni i parametri di primo approccio possono essere:

• Tensione d’ingresso V_I=325V;
• Tensione d’uscita V_O=12V;
• Rendimento η=0,85%;
• Massima corrente d’uscita I_O=1,3A;
• Frequenza di switching fs=132kHz.

La tensione d’uscita e la massima corrente in uscita sono i valori desiderati per il futuro alimentatore; perché la scheda del monitor prevede un’alimentazione a 12V e un assorbimento – comprendendo l’amplificatore audio al massimo volume – di circa 1,3A. Il rendimento lo imponiamo ad un valore tipico – né troppo basso, ma nemmeno troppo alto – salvo poi verificarne la veridicità. La frequenza di switching la si può desumere dalle caratteristiche del “trasformatore” che si vuole utilizzare nel primo prototipo (leggere oltre).

In base ai dati riportati il periodo della frequenza di switching è pari a:

T_S=\frac{1}{f_S}=\frac{1}{132 \times 10^5}=7,575 \times 10^{-6}=7,575μs

La potenza d’uscita richiesta dovrà essere di valore:

P_O=V_O \times I_O=12 \times 1,3=15,60W

e, avendo ipotizzato un rendimento η pari a 0,85, è possibile risalire alla presunta potenza richiesta alla sorgente d’ingresso; presunta perché occorrerà poi effettivamente verificare che il rendimento sia proprio l’85%.

P_I=\frac{P_O}{η}=\frac{15,60}{0,85}=18,35W

Si definisce duty-cycle il valore D rapporto tra il tempo nello stato di ON dello SW e il periodo della frequenza di switching:

D=\frac{t_{on}}{T_S}

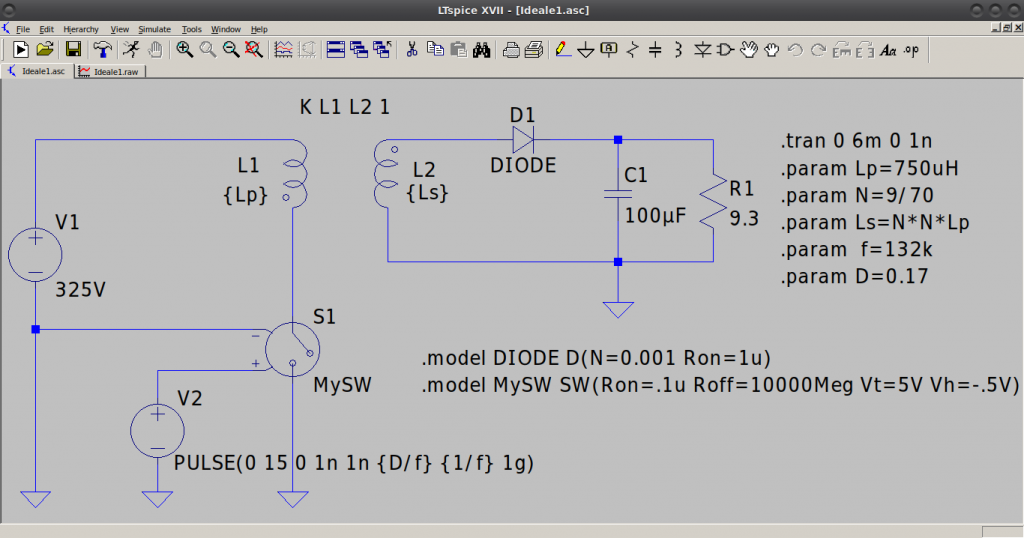
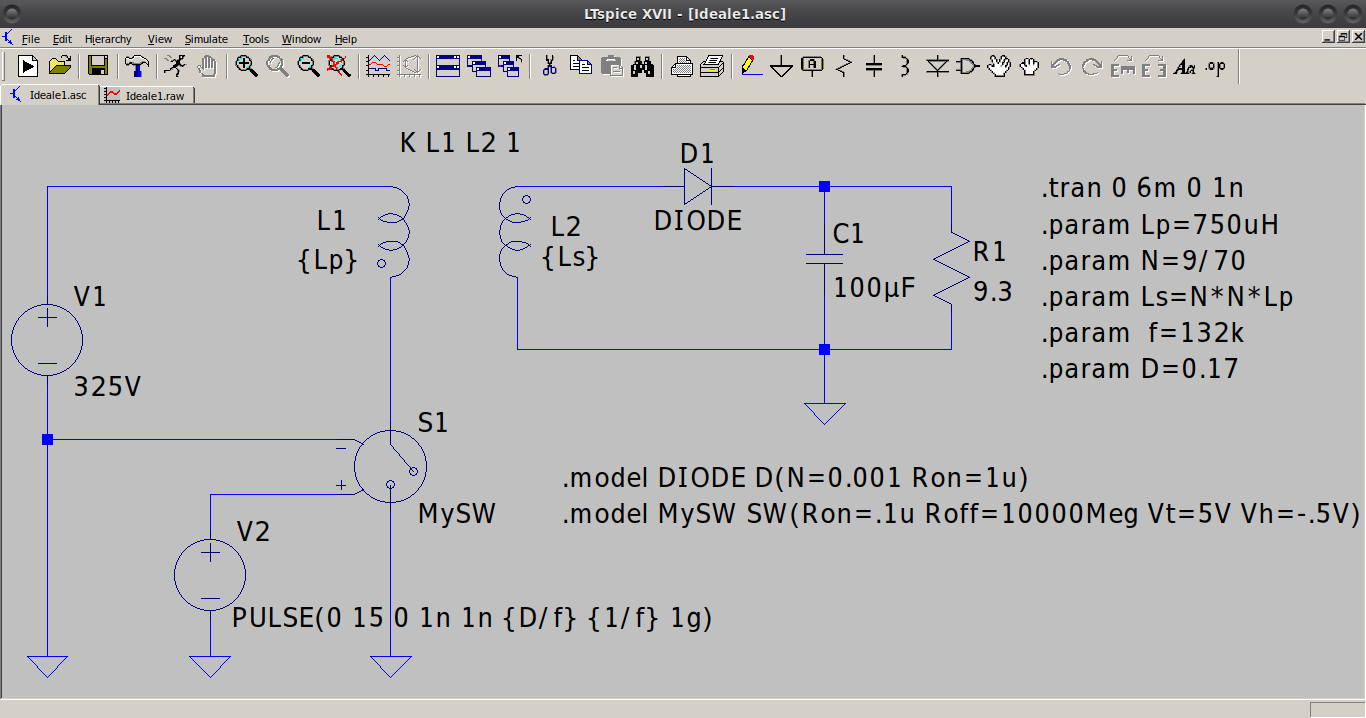
Il circuito ideale in esame è riportato nell’immagine in basso nel quale si considera la tensione di ingresso fissa a 325V, lo SW ideale pilotato da un generatore ideale di onda quadra 0V-15V a 132kHz con duty-cycle uguale a 0,17 (leggere oltre per il calcolo del duty-cycle in funzione del carico e di altri parametri). Anche il “trasformatore” in questa prima fase viene considerato ideale, come è evidente poiché presenta un fattore di accoppiamento K=1. In buona sostanza il trasformatore implementato nella simulazione è un classico modello a T nel quale viene considerata solo l’induttanza di magnetizzazione L_m pari a 750μH seguita da un trasformatore ideale con numero di spire pari a 70 al primario e 9 al secondario. Anche il diodo è considerato ideale così come il condensatore d’uscita nel quale non viene riportato uno dei parametri tipici per questo componente utilizzato in un SMPS, ovvero la ESR (Equivalent Series Resistance).

Si fa notare che il valore dell’induttanza e del numero di spire, e di riflesso il rapporto spire, non è casuale ma ho preso come riferimento un “trasformatore” reale MYRRA modello 74030 caratterizzato da 4 avvolgimenti: un primario, un avvolgimento ausiliario e due secondari come da datasheet riportato in basso e relative fotografie che danno conto della grandezza dello stesso.

---

Flyback12V1.3ATrasformatoreMYRRA74030

---

Gli stati del flyback DCM

Siccome verrà posta l’attenzione su un flyback che lavora in modalità DCM – e vedremo quali saranno le condizioni affinché la si debba e possa assicurare – è necessario sapere che questa modalità è caratterizzata da 3 stati di funzionamento:

1. Lo SW è in ON e il diodo D è in OFF; ciò avviene per 0<t≤D*T_S;
2. Lo SW è in OFF e il diodo D è in ON; ciò avviene per D*T_S<t≤(D+D₁)*T_S;
3. Lo SW è in OFF e il diodo D è in OFF; ciò avviene per (D+D₁)*T_S<t≤T_S.

Quando 0<t≤D*T_S

In condizioni di regime, poiché si sta analizzando la modalità DCM, all’istante t=0, punto di inizio della fase t_on, la corrente è uguale a 0. La tensione che insiste ai capi dell’induttanza L_m è la tensione di ingresso V_I di valore costante (si ipotizza nulla la caduta sullo SW), pertanto dalla relazione costitutiva di una induttanza si può scrivere:

v_{Lm}=V_I=L_m \frac{di_{Lm}}{dt}

laddove i_Lm(0)=0. Ma la corrente che circola in L_m circola anche nello SW pertanto:

i_{SW}=i_{Lm}=\frac{1}{L_m}\int_0^t v_{Lm}(t) dt=\frac{1}{L_m}\int_0^t v_I(t) dt=\frac{V_I}{L_m}t\kern{1cm}(1)

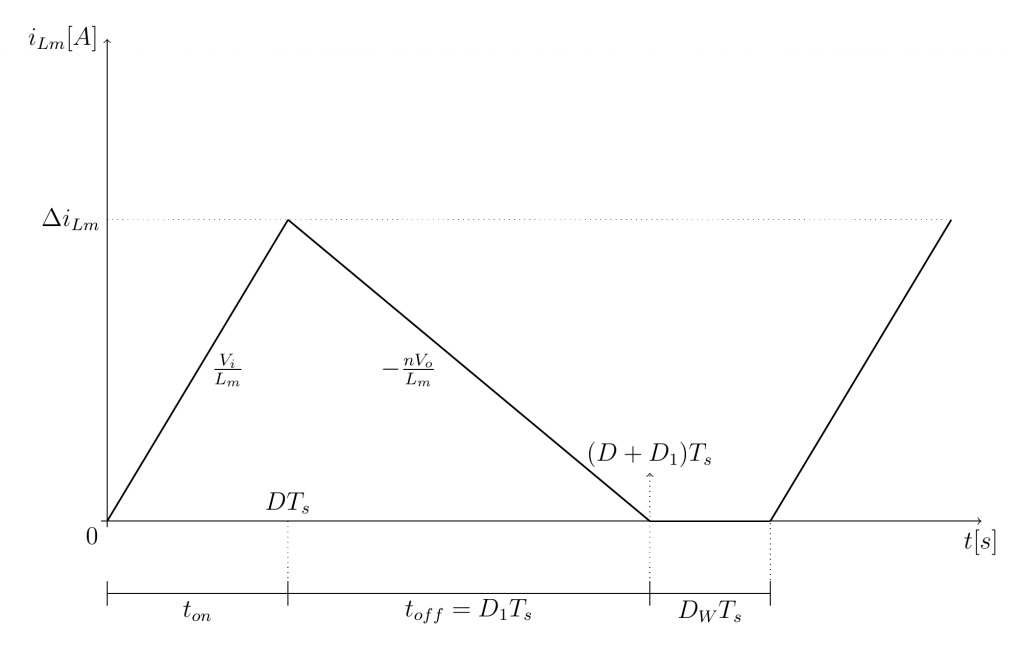
con \frac{V_I}{L_m} coefficiente angolare della retta nella fase di carica dell’induttore, vedere immagine in basso ottenuta con un semplice sorgente \TeX - \LaTeX seguendo un approccio uguale a quanto già visto per l’articolo Onda trapezoidale: disegnarla in TeX-LaTeX. Il valore massimo viene raggiunto al termine della fase di ON all’istante t=D*T_S e pertanto dalla (1) risulta che il valore di picco della corrente al primario – ovvero il valore massimo della corrente nello SW coincidente con il valore massimo della corrente nell’induttore – assume la forma (ricordando che il valore iniziale è pari a 0, si è in modalità DCM):

I_{Pk_{Prim}}=I_{SW_M}=i_{Lm_M}=\Delta i_{Lm}=\frac{V_I D T_S}{L_m}=\frac{V_I D}{L_m f_S}\kern{1cm}(2)

In queste condizioni la tensione ai capi del secondario del “trasformatore” è pari a:

v_2=-\frac{v_1(t)}{n}=-\frac{V_I}{n}

mentre la tensione ai capi del diodo D è data, applicando la LKT sulla maglia d’uscita:

v_D=- \left(\frac{V_I}{n}+V_O \right)

dalla quale è possibile ricavarne il valore massimo in modulo:

V_{D_{M}}=\frac{V_{I_{M}}}{n}+V_O\kern{1cm}(3)

 

Quando D*T_S<t≤(D+D₁)*T_S

In questo lasso di tempo lo SW è in OFF mentre il diodo D è in ON ciò implica, com’è facile intuire, che I_SW=0 e v_D=0 (diodo ideale) e ai capi dell’induttanza secondaria –  ovvero del carico, avendo considerato il diodo D ideale – risulterà v₂=V_O. Tale tensione si rifletterà – invertita, ricordare sempre la posizione dei “pallini” nella coppia di induttori – al primario quindi anche sulla L_m:

v_1=v_{Lm}=-n v_2=-n V_O=v_{Lm}=L_m \frac{di_{Lm}}{dt}\kern{1cm}(4)

Ma all’istante t=D*T_S risulta:

i_{Lm}|_{t=DT_S}=i_{Lm}(DT_S)

e, riprendendo l’equazione integrale presente nella (1), utilizzando la quarta uguaglianza vista da destra verso sinistra della (4) e facendo uso del risultato della (2), si può scrivere:

i_{Lm}=\frac{1}{L_m}\int_0^t v_{Lm}(t) dt=\frac{1}{L_m}\int_0^{DT_S} v_{Lm}(t) dt+\frac{1}{L_m}\int_{DT_S}^t v_{Lm}(t) dt=\\[1.5em]=i_{Lm}(DT_S)+\frac{1}{L_m}\int_{DT_S}^t v_{Lm}(t) dt=\frac{V_I D}{L_m f_S}+\frac{1}{L_m}\int_{DT_S}^t (-n V_O)dt=\\[1.5em]=\frac{V_I D}{L_m f_S}-\frac{nV_O}{L_m}(t-DT_S)\kern{1cm}(5)

Il risultato vede il valore massimo raggiunto all’istante t=D*T_S al quale si sottrae il secondo termine funzione del tempo; all’atto pratico una retta con coefficiente angolare negativo -\frac{n V_O}{L_m} come riportato nella figura precedente, valore che scende fino a 0 (in modalità DCM) all’istante (D+D₁)*T_S.

Per considerazioni successive ritorna utile valutare la variazione della i_Lm ovvero il secondo integrale – il secondo addendo – della (5) con estremi di integrazione D*T_S e (D+D₁)*T_S:

\Delta i_{Lm}=\frac{1}{L_m}\int_{D T_S}^{(D+D_1)T_S}v_{Lm}(t)dt=\frac{1}{L_m}\int_{D T_S}^{(D+D_1)T_S}-n V_O dt=\\[1.5em]=-\frac{1}{L_m}\int_{(D+D_1)T_S}^{D T_S}-n V_O dt=\frac{n V_o}{L_m}\int_{(D+D_1)T_S}^{D T_S} dt=\\[1.5em]=\frac{N V_o}{L_m}[D T_S-(D+D_1)T_S]=\frac{n V_O D_1}{L_m f_S}

NOTA: nella precedente dimostrazione nel passare dal primo al secondo rigo si è fatto uso di una nota proprietà degli integrali:

\int_a^b f(x)dx=-\int_b^a f(x)dx

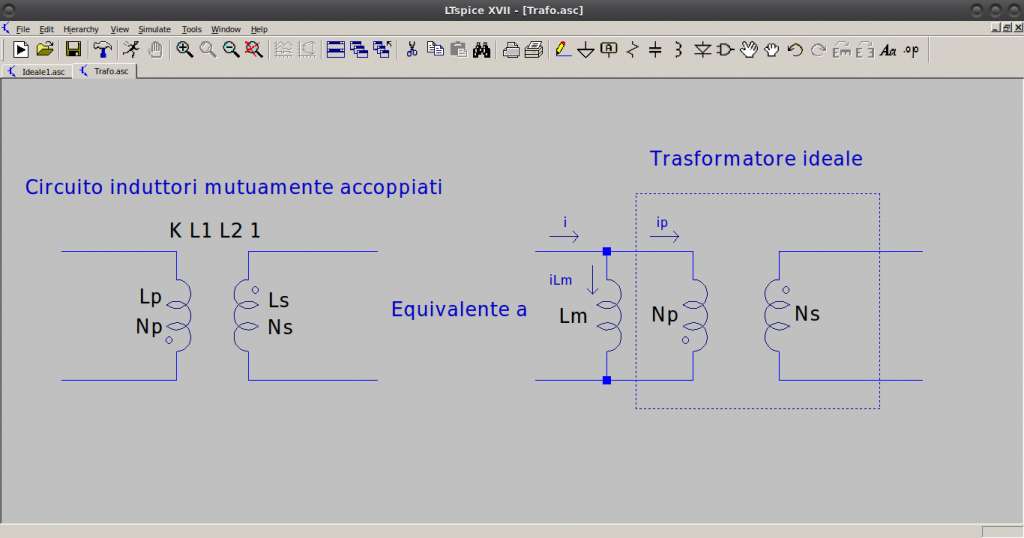
Prima di fare un ulteriore passo avanti occorre fare una considerazione sul circuito utilizzato nella simulazione. Per la simulazione di trasformatori è possibile utilizzare alcune metodologie, la più immediata è tramite l’utilizzo di induttori mutuamente accoppiati utilizzando la direttiva K L1 L2 1, ad indicare un accoppiamento perfetto – valore K=1 – tra l’induttore L1 e l’induttore L2 (tutte le linee di flusso generate da un avvolgimento vanno a concatenarsi con l’altro avvolgimento). Questa rappresentazione dal punto di vista pratico implica l’ipotizzare un trasformatore ideale con avvolgimenti a fasi contrapposte (come è evidente, ancora una volta dal posizionamento dei “pallini” sugli induttori). Ma un trasformatore ideale può essere anche rappresentato come visibile in basso in figura; l’induttanza di magnetizzazione e un sistema ideale di trasformazione con rapporto spire pari a n=Np/Ns. Dal punto di vista circuitale non cambia assolutamente niente.

Infatti, poiché in questa fase lo SW è in OFF, allora l’unica maglia chiusa al primario è proprio quella tra l’induttanza di magnetizzazione Lm e l’ideale trasformatore con Np spire primarie il che comporta, applicando la LKC e considerando il risultato della (5):

i_{Prim}=-i_{Lm}=\frac{n V_O}{L_m}(t-D T_S)+\frac{n V_I D}{L_m f_S}\kern{1cm}(6)

Va da se come in un flyback reale non è possibile osservare la corrente dell’induttanza di magnetizzazione Lm poiché non fisicamente accessibile, come noto è una “astrazione” ottenuta nel ricavarsi il circuito equivalente del trasformatore.

Questo risultato può essere confermato – e verificato – attraverso la simulazione del circuito. Nell’immagine in basso a sinistra segue in colore verde la corrente nell’induttanza primaria L1, in colore rosso la corrente nell’induttanza di secondario L2. In blu la corrente nell’induttanza di magnetizzazione Lm con corrente secondaria riportata al primario (osservare il rapporto spire riportato nella formula in alto al centro del diagramma) e sommata algebricamente alla corrente in L1. Si può notare come il risultato sia assolutamente il medesimo della figura precedente ottenuta con passaggi analitici (figura creata ad-hoc in \TeX - \LaTeX).

Il tempo tra le due linee verticali in viola indica:

1. Che il sistema – a regime – sta lavorando effettivamente in modalità DCM; la corrente nell’induttanza di magnetizzazione va a 0 – linea viola a sinistra – prima dell’inizio del periodo successivo (linea viola a destra);
2. A partire dall’istante di tempo indicato con la linea viola di sinistra inizia la terza modalità di funzionamento del flyback DCM, modalità riportata nel seguito.

Quale dei due comportamenti preferire in presenza di simulatori (e.g. TopSPice) che possono mettere a disposizioni entrambe le rappresentazioni? Per quanto mi riguarda è indifferente, l’importante è non cadere “nel tranello” della rappresentazione degli induttori mutuamente accoppiati i quali, prima che venga raggiunta la condizione di regime, “illudono” che la corrente primaria sia pari a 0 quando lo SW commuta in OFF (curva verde in basso nell’immagine di destra). Non è così! La reale rappresentazione della corrente primaria è quella della corrente nell’induttanza di magnetizzazione Lm che evidenzia una modalità di funzionamento CCM (Continuous Conduction Mode) fino alla condizione di regime (poco più di 120μs in questa simulazione); altrimenti detto in questa prima fase si ha circolazione di corrente al primario anche quando lo SW è in OFF almeno fino a quando non si stabilisce una condizione di regime (figura di sinistra in blu o figura di destra in blu superati i 120μs).

Il passo successivo vede la valutazione della corrente nel secondario e quindi nel diodo D. Ricordando il risultato ottenuto nella (6) è possibile scrivere:

i_D=i_{Sec}=-ni_{Prim}=-\frac{n^2 V_O}{L_m}(t-D T_S)+\frac{n V_I D}{L_m f_S} \kern{1cm}(7)

Il valore di picco di corrente nel diodo D avviene all’atto della commutazione e, ricordando il risultato ottenuto nella (2), è pari a:

I_{D_M}=n I_{SW_M}=n I_{Pk_{Prim}}=\frac{n V_I D}{L_m f_S}\kern{1cm}(8)

Indicando con v_Prim la tensione ai capi dell’avvolgimento primario, considerando che la tensione al secondario viene riflessa al primario attraverso il rapporto di trasformazione v_{Prim}=-n v_{Sec}=-n V_O, l’applicazione della LKT alla maglia di ingresso permette di valutare il valore della tensione ai capi del SW:

v_{SW}=V_I - v_P=V_I + n V_O\kern{1cm}(9a)

il cui valore massimo è:

V_{SW_M}=V_{I_M}+n V_O\kern{1cm}(9b)

Quando (D+D₁)*T_S<t≤T_S

In questa fase l’energia magnetica immagazzinata nel nucleo nel tempo t_on è esaurita pertanto il diodo D va in interdizione. Ancora non è iniziato un nuovo ciclo quindi anche lo SW è in OFF, questo comporta:

• i_D=i_Sec=0;
• i_Prim=i_SW=i_Lm=0;
• v_SW=V_I;
• v_D=-V_O;

alle quali aggiungere, come diretta conseguenza della seconda, v_{Prim}=v_{Lm}=L_m \frac{di_{Lm}}{dt}=0, equazione che conclude l’analisi di questo stato di funzionamento.

Primi risultati

Ora che si hanno le prime serie di formule e una simulazione a disposizione – con annessi risultati – si può verificare il valore tra le formule teoriche e la simulazione di un circuito ideale a componenti ideali.

Dalla (2) è possibile ricavarsi la corrente di picco primario sostituendo i valori al posto dei parametri:

I_{Pk_{Prim}}=\frac{V_I D}{L_m f_S}=\frac{325\times 0,17}{750\times 10^{-6}\times 1,32\times 10^5}=0,558A

risultato che confrontato con la figura di sinistra della precedente galleria fotografica evidenzia come in simulazione il cursore posizionato sul picco della corrente primaria al termine di t_on riporti circa 558,61mA in perfetto accordo con quanto fin qui calcolato.

La seconda verifica riguarda la tensione massima ai capi del diodo. Per la valutazione del valore si deve utilizzare la (3) nella quale V_{I_{M}}=V_I=325V. Sostituendone i valori risulta:

V_{D_{M}}=\frac{V_{I_{M}}}{n}+V_O=\frac{325}{\frac{70}{9}}+12=53,79V

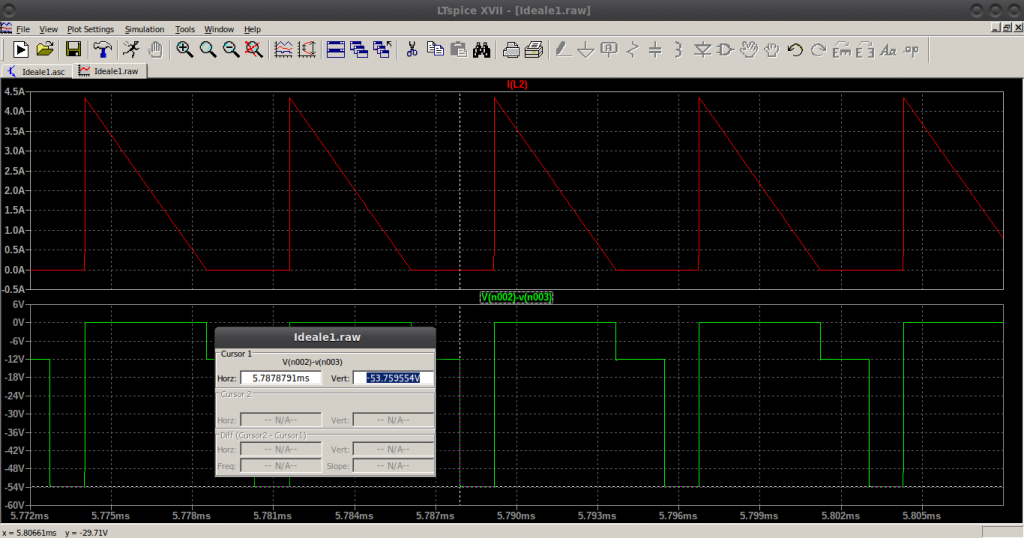
ovvero in condizioni ideali il diodo D deve essere in grado di bloccare una tensione di circa 54V. Si può verificare il risultato in simulazione sottraendo il potenziale anodico al potenziale catodico e ottenendo quanto riportato di seguito:

 

Quando il diodo D è in conduzione – corrente i_L2 diversa da 0 – la tensione ai capi del diodo è 0V, come deve essere essendo il diodo ideale. Quando la corrente arriva a 0 il diodo si interdice e su di esso insiste la tensione d’uscita di 12V che lo polarizza inversamente. Appena si riattiva lo SW, nel periodo successivo, ecco che la tensione vista ai capi del secondario è negativa (ricordare sempre la posizione dei “pallini” sugli induttori) e di valore ridotta del rapporto di trasformazione n; tale tensione rafforza la polarizzazione inversa del diodo facendola arrivare ai circa 54V della curva verde, valore pienamente compatibile con il risultato calcolato.

Altro parametro ricavato nella teoria fin qui analizzata è la tensione ai capi dello SW. È evidente come in fase di ON il suo valore risulti pari a 0 essendo ideale; in questa fase l’SW è sollecitato dal dover “reggere” il valore della corrente primaria calcolata in precedenza. Ma un’ulteriore sollecitazione arriva nella fase di OFF dovuta alla tensione riportata nella (9b). Sostituendo i valori ai parametri risulta:

V_{SW_M}=V_{I_M}+n V_O=325+\frac{90}{7}12=418,33V

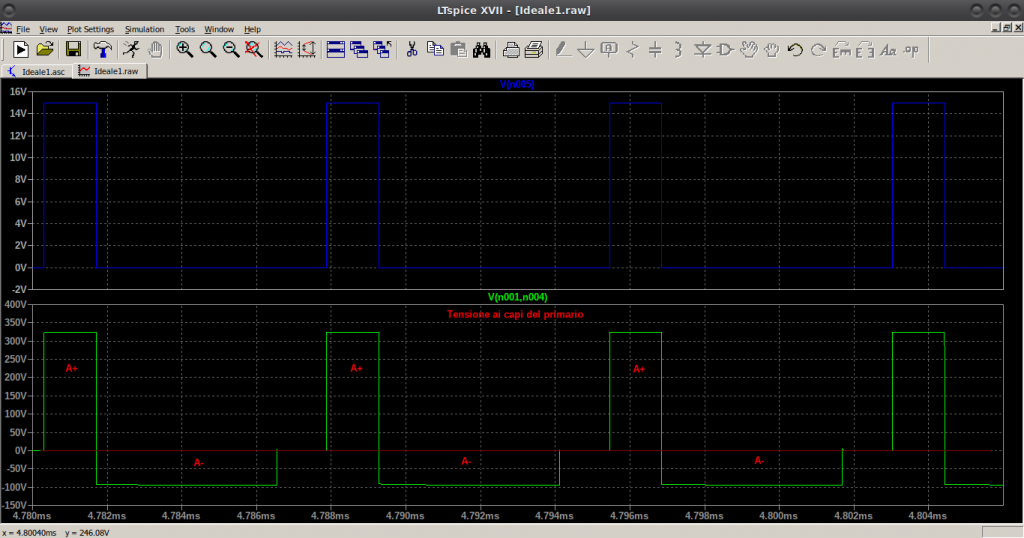
laddove il secondo addendo indica la cosiddetta tensione di flyback riflessa al primario dal secondario che va a sommarsi a quella presente sullo SW nella fase di OFF – pari alla piena 325V – per un totale di circa 418V, valore confermato dalla simulazione (curva verde in basso):

Finché il diodo D è in conduzione si ha la totale tensione riflessa che va a sommarsi alla tensione di linea livellata. Quando il diodo si interdice appare “solo” la tensione di linea (325V). Un prima conclusione allora vede il MOSFET/IGBT/BJT, che poi implementerà l’SW, dover riuscire a bloccare una tensione drain-source/collettore-emettitore di almeno 420V (in realtà si vedrà come rimuovendo alcune condizioni di idealità tale tensione potrà raggiungere e superare abbondantemente i 600V!).

Al netto di altri parametri, rimane ancora almeno un aspetto da dover dimostrare: da dove viene fuori il valore del duty-cycle pari a 0,17 inserito nelle formule e nella simulazione? Anche perché il valore della tensione d’uscita a regime è esattamente quello voluto! Per capirlo occorre valutare il valore di D in funzione dei parametri.

Fdt in continua flyback DCM e valutazione di D

La tensione ai capi dell’avvolgimento primario è pari al valore di linea rettificato (325V) quando lo SW è nella fase di ON mentre è pari alla negativa della tensione riflessa quando lo SW è in OFF e finché il diodo al secondario è in ON. In condizioni di regime l’area sottesa nella fase di OFF deve essere uguale all’area sottesa nella fase di ON. In altre parole, dall’immagine in basso della differenza di potenziale al primario del “trasformatore” (curva verde), dovrà risultare A+=A- (la curva blu indica il tempo di ON e OFF dello SW).

 

La condizione di uguaglianza delle aree porta a scrivere:

V_I D T_S=n V_O D_1 T_S \Rightarrow V_I D=n V_O D_1 \Rightarrow \frac{V_O}{V_I}=\frac{D}{n D_1}

In assenza di perdite (rendimento 100%) è evidente come si abbia P_O=P_I ovvero V_O*I_O=V_I*I_I che per la precedente è possibile riscrivere come:

\frac{V_O}{V_I}=\frac{I_I}{I_O}=\frac{D}{n D_1}\kern{1cm}(10)

Con la (7) è stata valutata la dipendenza della corrente nel diodo D, e quindi della corrente secondaria, in funzione di alcuni parametri tipici. Ricordando la definizione di valore medio quel risultato ci permette di ottenere il valore medio della corrente d’uscita che poi coincide con il valore medio della corrente che attraversa il carico. Nella valutazione occorre ricordare che il diodo è in ON tra D*T_S<t≤(D+D₁)*T_S, pertanto:

I_{o} \triangleq \frac{1}{T} \int_0^T i_D(t) dt=\frac{1}{T_S} \int_{DT_S}^{(D+D_1)T_S} i_D(t) dt=\\[1.5em]=\frac{1}{T_S} \int_{DT_S}^{(D+D_1)T_S} \left [-\frac{n^2 V_O}{L_m} (t-D T_S) + \frac{n V_I D}{L_m f_S} \right] dt=\\[1.5em]=-\frac{1}{T_S} \int_{DT_S}^{(D+D_1)T_S} \frac{n^2 V_O}{L_m} t dt+ \frac{1}{T_S} \int_{DT_S}^{(D+D_1)T_S} \frac{n^2 V_O}{L_m} D T_S dt+\frac{1}{T_S} \int_{DT_S}^{(D+D_1)T_S} \frac{n V_I D}{L_m f_S} dt=\\[1.5em]=-\frac{1}{2 T_S} \frac{n^2 V_O}{L_m} t^2|_{D T_S}^{(D+D_1)T_S}+\frac{n^2}{T_S} \frac{V_O D T_S}{L_m} t|_{D T_S}^{(D+D_1)T_S}+\frac{n}{T_S} \frac{V_I D}{L_m f_S} t|_{D T_S}^{(D+D_1)T_S}=\\[1.5em]=-\frac{1}{2 T_S} \frac{n^2 V_O}{L_m} \{[(D+D_1)T_S]^2 - D^2 T_S^2  \}+\frac{1}{T_S} \frac{n^2 V_O D T_S}{L_m}[(D+D_1)T_S - D T_S]+\\[1.5em]+\frac{1}{T_S} \frac{n V_I D}{L_m f_S}[(D+D_1)T_S - D T_S]=-\frac{1}{2 T_S} \frac{n^2 V_O}{L_m} \{D_1^2 T_S^2 + 2 D D_1 T_S^2  \}+\\[1.5em]+\frac{1}{T_S} \frac{n^2 V_O D T_S}{L_m} D_1 T_S +\frac{n}{T_S} \frac{V_I D}{L_m f_S} D_1 T_S=-\frac{1}{2 T_S} \frac{n^2 V_O D_1^2 T_S^2}{L_m}+\\[1.5em]\cancel{-\frac{1}{\cancel{2} T_S} \frac{n^2 V_O \cancel{2} D D_1 T_S^2}{L_m}}+\cancel{\frac{1}{T_S} \frac{n^2 V_O D D_1 T_S^2}{L_m}}+\frac{n}{T_S} \frac{V_I D D_1 T_S}{L_m f_S}=\\[1.5em]=-\frac{1}{2} \frac{n^2 V_O D_1^2 T_S}{L_m}+\frac{n V_I D D_1}{L_m f_S}

ma dalla (10) è possibile ricavare la tensione d’uscita:

V_O=\frac{D V_I}{n D_1}

che sostituita nel risultato precedente fornisce:

I_O=-\frac{1}{2} \frac{n^2 V_I D_1^2 T_S}{n D_1 L_m}+\frac{n V_I D D_1}{L_m f_S}=-\frac{1}{2} \frac{n^2 D V_I D_1^2 T_S}{n D_1 L_m}+\frac{n V_I D D_1}{L_m f_S}=\\[1.5em]=-\frac{1}{2} \frac{n D V_I D_1 T_S}{L_m}+\frac{n D V_I D_1 T_S}{L_m}=\frac{1}{2} \frac{n D V_I D_1}{L_m f_S}

Il valore medio della corrente sul carico R_L è pari a I_O=\frac{V_O}{R_L} che eguagliato al risultato precedente:

\frac{n D D_1 V_I}{2 L_m f_S}=\frac{V_O}{R_L} \Rightarrow FDT_{V_{DC}}=\frac{V_O}{V_I}=\frac{n D D_1 R_L}{2 L_m f_S}

ovvero, ricordando sempre la (10):

\frac{\cancel{D}}{n D_1}=\frac{n \cancel{D} D_1 R_L}{2 L_m f_S} \Rightarrow D_1^2=\frac{2 L_m f_S}{n^2 R_L}

D_1=\sqrt{\frac{2 L_m f_S}{n^2 R_L}}=\sqrt{\frac{2 L_m f_S I_O}{n^2 V_O}}\kern{1cm}(11)

Sostituendo la (11) nella (10) si ha come risultato:

\frac{V_O}{V_I}=\frac{I_I}{I_O}=\frac{D}{n \sqrt{\frac{2 L_m f_S I_O}{n^2 V_O}}}=\frac{\cancel{n} D}{\cancel{n}} \sqrt{\frac{V_O}{2 L_m f_S I_O}}=\\[1.5em]=FDT_{V_{DC}}=D \sqrt{\frac{R_L}{2 L_m f_S}}\kern{1cm}(12)

La (12) permette di ricavare il duty-cycle D in funzione dei parametri del convertitore:

D=FDT_{V_{DC}} \sqrt{\frac{2 L_m f_S I_O}{V_O}}=\frac{V_O}{V_I}\sqrt{\frac{2 L_m f_S}{R_L}}\kern{1cm}(13a)

Tenendo conto della (11) va da se che per rimanere in modalità DCM il valore del duty-cycle D non potrà che essere:

D \lt 1-D_1=1-\sqrt{\frac{2 L_m f_S I_O}{n^2 V_O}}=1- \sqrt{\frac{2 L_m f_S}{n^2 R_L}}\kern{1cm}(13b)

Altri risultati

La formula (13a) ci fornisce il valore del duty-cycle in funzione dei parametri:

D=\frac{V_O}{V_I}\sqrt{\frac{2 L_m f_S}{R_L}}=\frac{12}{325}\sqrt{\frac{2 \times 750 \times 10^{-6} \times 1,32 \times 10^5}{9,3}}=0,17

ovvero il valore del duty-cycle D da utilizzarsi – e utilizzato – in simulazione e tale da fornire in uscita i 12V richiesti così come riportato nella figura in basso.

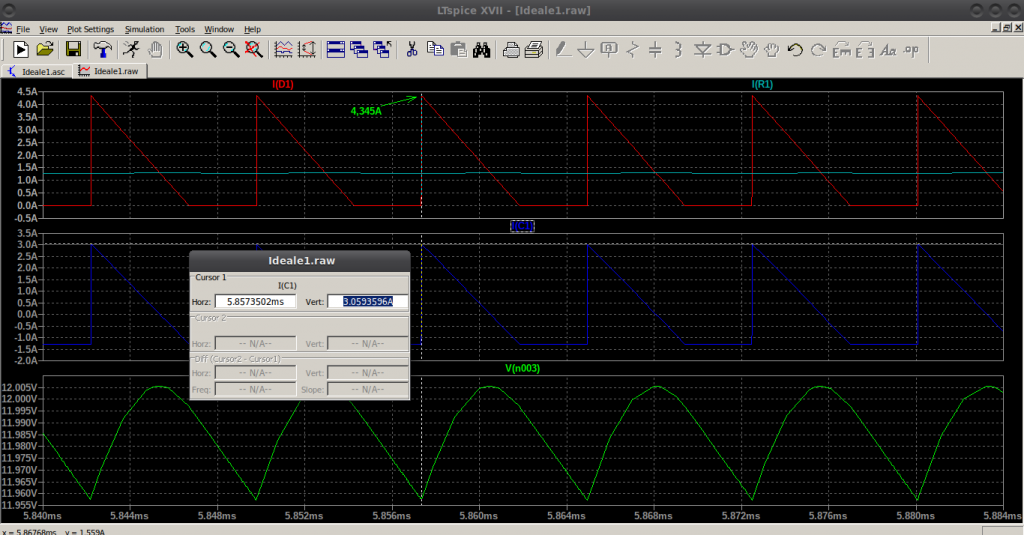
In curva in rosso è la corrente che attraversa il diodo: notare il “salto” alla fine del tempo di ON dello SW. Questo gradino netto è dovuto, oltre al fatto che si è in condizioni ideali, al rapporto spire del “trasformatore”. Infatti dalla (8), ricordando che la corrente di picco primaria è stata calcolata in precedenza di valore pari 0,558A, risulta:

I_{D_M}=n I_{Pk_{Prim}}=\frac{70}{9} \times 0,558=4,34A

valore assolutamente congruente con la simulazione (4,345A).

La evidente discontinuità nella corrente induce un ripple (ondulazione) sulla tensione d’uscita persino quando – come in questo caso – la capacità d’uscita è ritenuta ideale. Questo comportamento non deve sorprendere poiché quando il diodo D è in OFF sarà proprio la capacità C a fornire la corrente necessaria al carico portando il condensatore a scaricarsi. Questo comportamento è chiaramente riportato nell’andamento della corrente della capacità con la curva blu: quando il diodo è interdetto il condensatore garantisce la corrente di 1,3A necessaria al carico, infatti è negativa (“esce” dalla capacità). Quando il diodo va in conduzione il condensatore verrà ricaricato a partire da una corrente di picco di circa 3,06A (rigo Vert: evidenziato in blu nella piccola finestra di pop-up in primo piano) la quale sommandosi alla corrente media necessaria al carico (1,3A) raggiunge il picco di circa 4,3A visibile nella curva rossa.

L’ondulazione sulla tensione d’uscita vedrà un’ulteriore degradazione nel momento in cui verrà considerata la ESR del condensatore.

Termina qui questa prima parte. Nella prossima puntata oltre a riportare ulteriori considerazioni teoriche tali da ampliare le conoscenze fin qui acquisite, verranno rimosse alcune condizioni di idealità e si valuterà il comportamento di un primo rudimentale montaggio pratico con tutte le attenzioni del caso essendo un circuito alimentato dalla tensione di rete livellata.