Chi ha detto che occorre per forza Excel per svolgere un certo numero e tipo di funzioni comunque complesse? Diversi soggetti vorrebbero far credere che Microsoft Excel sia praticamente l’unico programma di foglio di calcolo sul pianeta che valga la pena usare. L’affermazione potrebbe essere veritiera se si necessita di macro pregresse scritte in VBA (Visual Basic for Applications) ma oramai, con le nuove versioni di LibreOffice, ha perso la sua veridicità anche sulle tabelle Pivot gestite e create in maniera ottimale dalla suite libera.

Le funzioni supportate sono comparabili con il corrispondente software proprietario e nel seguito verrà riportato come rappresentare la risposta armonica di un sistema previa rappresentazione dei diagrammi di Bode e del corrispondente diagramma di Nyquist della medesima funzione di trasferimento.

Introduzione

Da diverso tempo a questa parte il team di LibreOffice festeggia nuovi record di download ad ogni nuovo rilascio (anche “minor”). Ne hanno ben donde perché la suite per ufficio open source più famosa, sebbene non l’unica nel mondo open source, ha raggiunto notevoli traguardi con continui miglioramenti, sotto ogni punto di vista, ad ogni nuovo rilascio.

Per completezza si vuole qui ricordare anche altri progetti che rientrano della definizione di “suite/programmi per ufficio” e sviluppati nel mondo open source. Gli interessati possono provare l’intera suite Calligra associata all’ambiente KDE, così come “progetti individuali” ma che presi insieme realizzano un gruppo di programmi per ufficio e non solo; è il caso “dell’ambiente del piedone” Gnome, con il foglio di calcolo Gnumeric , il word processor AbiWord, il software di grafica vettoriale Inkscape e altri componenti.

Ritornando a LibreOffice, arrivata, al momento di scrivere queste righe, alla versione 7.3.2, LibreOffice è in grado di mostrare tutta la sua maturità e pienezza di funzioni raggiungendo un livello che non ha nulla da invidiare a soluzioni proprietarie blasonate. Nel caso specifico il riferimento è al foglio elettronico Calc con il quale è possibile compiere operazioni complesse senza necessità alcuna di dover ricorrere ad “altro”.

Nell’ottica dell’argomento che si affronterà, nel seguito si farà notare come le funzioni supportate siano assolutamente comparabili con corrispondenti software proprietari. L’obiettivo di questo articolo è mostrare la rappresentazione della risposta armonica G(\jmath\omega) di un sistema lineare, stazionario a tempo continuo ovvero la caratteristica d’uscita di un sistema in regime permanente in risposta ad una sinusoide di pulsazione ω applicata all’ingresso.

Trattasi di una funzione complessa (nel senso di piano complesso e numeri complessi) di variabile reale che per \omega \in \Re^+ descrive il comportamento del sistema al variare della pulsazione ovvero, a meno di 2π, della frequenza. Due le rappresentazioni possibili;

• Cartesiana: G(\jmath\omega)=Re[G(\jmath\omega)]+Im[G(\jmath\omega)]
• Polare: G(\jmath\omega)=|G(\jmath\omega)| \times e^{\jmath\phase{G(\jmath\omega)}}

Si può quindi far uso di diagrammi al fine di poter rappresentare la funzione di risposta armonica in termini di ampiezza e fase. Su due diagrammi; una rappresentazione polare della risposta armonica mediante due diagrammi semilogaritmici uno per il modulo e uno per la fase così come analizzato nell’articolo I diagrammi di Bode. La seconda rappresentazione vede il tracciamento del diagramma di Nyquist, un’unica curva parametrizzata in ω nel piano complesso ovvero la rappresentazione cartesiana della funzione di risposta armonica della funzione di trasferimento in esame che definisce il cosiddetto “percorso di Nyquist” (percorso chiuso). L’applicazione del criterio di Nyquist al suddetto percorso permette di dedurre la stabilità di un sistema ad anello chiuso a partire dalle informazioni relative al sistema ad anello aperto, che negli esempi che seguiranno potrà essere rappresentato dalla f.d.t. che si andrà a prendere in considerazione così come ampiamente riportato nell’articolo Criterio di stabilità di Nyquist.

LibreOffice Calc, a differenza di altri programmi come Scilab, Matlab o applicazioni on-line come Wolfram Alpha, che una volta fornita la funzione di trasferimento vanno “avanti da soli” grazie alla presenza di macro appositamente realizzate, effettua i grafici in funzione dei dati che di volta in volta, passo dopo passo, vengono ottenuti. Naturalmente niente e nessuno vieta lo sviluppo di una macro appositamente realizzata in linguaggio LibreOffice Basic che automatizzi tutto il processo una volta fornito il campo di valori e la funzione di trasferimento.

Sia che si utilizzi LibreOffice Calc o che si utilizzino programmi come Scilab &Co. i dati devono essere ben interpretati e, dando per scontato che i suddetti programmi non commettano errori (assenza di bug come oramai è auspicabile almeno per i diagrammi “storici”), occorre capire cosa si è ottenuto e riuscire a vedere anche “ad occhio” se c’è un errore dovuto, ad esempio, ad una errata immissione di una costante, di un dato ecc. In sostanza occorre sapere ciò che si sta facendo!

Gli esempi riportati in basso seguono lo stesso tipo di esempi riportato nell’articolo Criterio di stabilità di Nyquist; in sostanza “Esempio numero 1” qui presente coincide con l’esempio numero 1 del richiamato articolo, “Esempio numero 2” qui riportato è l’esempio 2 del citato articolo e così via a seguire. In questo modo si ha un immediato riscontro e verifica anche con Scilab evitando inutili ripetizioni e perdite di tempo.

Scale logaritmiche

La rappresentazione di valori positivi ad ampia variazione, come i valori della pulsazione ω [rad/s] (o della frequenza f [Hz], sono “uguali” a meno del fattore 2π), trova come grande alleata l’uso di scale logaritmiche. I valori riportati su una siffatta scala equivalgono al logaritmo in base 10 della grandezza, in formule:

X=\log_{10}(\omega) \Rightarrow \omega=10^X

dal quale è evidente come il valore della pulsazione ω risulti legato al valore X dalla formula “inversa” (proprietà logaritmi/esponenziali) riportata subito dopo. Questo comporta che volendo valutare la risposta di un sistema con valori della pulsazione che spaziano da 1/10 rad/s a 100 rad/s (in termini di frequenza significa spaziare da 15,9mHz a 15,9Hz) il valore della X dovrà essere compreso nel range -1≤X≤2. Questo concetto verrà utilizzato a breve.

Per quanto detto va da se che in una siffatta scala la posizione dei valori intermedi tra una potenza e la successiva altro non sono che i valori dei corrispondenti logaritmi in base 10. Questo vuole dire, ad esempio, che tra la potenza 1 e 10 il valore ω=2 è posizionato al valore corrispondente X=log₁₀(2)≅0,3010, il valore ω=3 in X=log₁₀(3)≅0,4771 quindi quasi al centro della distanza 1-10, per questo motivo via via che si va verso il 9 le suddivisioni in una scala logaritmica tendono ad addensarsi. Stesse considerazioni per il range di potenza tra 10-100; il valore ω=20 corrisponde a X=log₁₀(20)≅1,3010, ω=30 comporta X=log₁₀(30)≅1,4771 e così via a seguire. Una corrispondenza come visibile nella figura in basso.

IMMAGINE DA LATEX  [in preparazione]

 

A tal proposito occorre ricordare che le funzioni esponenziali come y₁=K*a^x su diagrammi semi-logaritmici (ovvero dove solo uno dei due assi ha una scala logaritmica) presentano un andamento lineare. Infatti la precedente funzione è possibile scriverla, ricordando le proprietà dei logaritmi:

\log_{10} y_1=\log_{10}(K a^x)=\log_{10}K+x\log_{10}a

che può essere riscritta come:

Y_1=\log_{10}K+X\log_{10}a

dopo aver posto Y₁=log₁₀ y₁ e X=x e che di fatto ci porta alla nota equazione di una retta y=q+mx. dove q=log₁₀ K e m=log₁₀ a.

Invece i diagrammi logaritmici, ovvero entrambi gli assi con scala logaritmica, hanno la capacità di linearizzare, nella rappresentazione, le funzioni potenza del tipo y₂=K*x^a, come è facile verificare seguendo la medesima dinamica precedente:

\log_{10} y_2=\log_{10}(K x^a)=\log_{10}K+a\log_{10}x

ovvero:

Y_2=\log_{10}K+a X

dopo aver posto Y₂=log₁₀ y₂ e X=log₁₀ x che porta di nuovo all’equazione della retta y=q+mx. dove q=log₁₀ K e m=a.

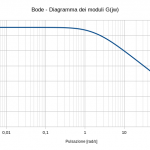
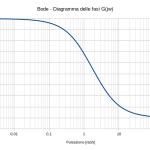
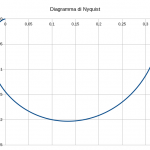
Esempio numero 1

Poiché la procedura si ripete identicamente per qualsiasi funzione di trasferimento si voglia rappresentare, solo per questo esempio ho realizzato un video. Un video purtroppo “muto” poiché tra le diverse strumentazioni, componentistica di ogni tipo a disposizione solo all’ultimo mi sono reso conto che a mancarmi è proprio un microfono! 🙂

Per tale motivo nel seguito sono commentati (mancando dell’audio) i passi che si vedono nel video e relativi alla f.d.t. ad anello aperto:

F(s)=\frac{1}{(s+1)(s+3)}

Il video al quale si fa riferimento è stato editato, per quel poco che è servito, utilizzando il programma open source di video editing OpenShot. La versione LibreOffice utilizzata è la 7.2.5.2.0+ in una distribuzione GNU/Linux Mageia 8. Il desktop del computer è stato ripreso utilizzando il software VokoscreenNG. La descrizione del video è subito in basso.

 

Nella colonna B viene riportato il valore dell’esponente della funzione esponenziale 10^x. Poiché si è interessati al comportamento del sistema che spazia da 0,001 rad/s a 1.000 rad/s ciò comporta un valore dell’esponente compreso nella gamma di valori -3≤x≤3. Se per ogni gruppo di potenza, e.g. da 10^-3 a 10^-2, vogliano rappresentare 100 valori allora ci occorrono 600 celle per contenere tutti i valori del campo completo da 10^-3 a 10³. Per ottenere 100 valori per ogni decade occorre incrementare l’esponente della funzione esponenziale di 0,01. Nessuno vieta di avere 1.000 valori per ogni decade (incremento di 1 millesimo per ogni passo), in questo caso il numero di celle che ricopre l’intera gamma di valori sarà pari a 6.000. Il come selezionare il numero di celle di cui si necessita e la compilazione automatica della serie di valori è chiaramente visibile nei primi 40 secondi del video.

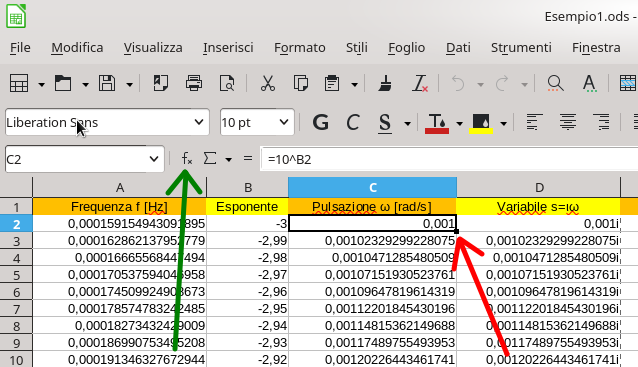
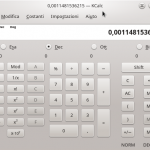
Nella colonna C è riportata la pulsazione ω ovvero il valore della funzione esponenziale 10^x al variare dell’esponente da -3 a 3 con incrementi di 0,01. Per questa funzione viene utilizzata la notazione 10^B2 per la prima cella che indica di elevare al valore della cella B2 il numero 10 quindi, di fatto, 10^-3=0,001. Questo per la prima cella, ma rimangono da riempire le rimanenti 599 celle con i rispettivi valori. Va da se che questo non lo si farà manualmente, ma verrà sfruttata la funzione di compilazione automatica. In sostanza dopo aver inserito il primo valore nella cella C2 sarà sufficiente spostare il cursore del mouse sulla maniglia della cella il quale cambierà forma da una freccia ad un +, quindi cliccare due volte. Per maniglia ci si riferisce al piccolo quadratino nero in basso a destra di una cella selezionata come chiaramente visibile nel video e indicato con una freccia rossa nella figura a lato (un click per ingrandirla). La verifica della correttezza dei risultati, come da immagine in basso, è immediata, infatti è sufficiente eseguire un calcolo con una comune calcolatrice; nella figura il valore di 10^-2,94.

Per la colonna D occorre creare un numero complesso puro, ovvero caratterizzato solo dalla parte immaginaria e che risulterà la variabile s=jω. Come riportato nel video ci si può aiutare con la Creazione guidata funzione, pulsante/icona indicato dalla freccia in nero nella figura precedente oppure, dopo aver selezionato la cella D2 premere F2 e scrivere il valore =COMPLESSO(0;C2) laddove la macro/funzione COMPLESSO(Re,Im,Suf) permette di convertire la parte reale e il coefficiente immaginario in un numero complesso. Siccome il valore reale è pari a 0 come immaginario è impostato il valore della pulsazione ω di fatto si ottiene il valore s=jω. Ancora una volta inserito il primo valore si sfrutterà la compilazione automatica per riempire in automatico le rimanenti 599 caselle.

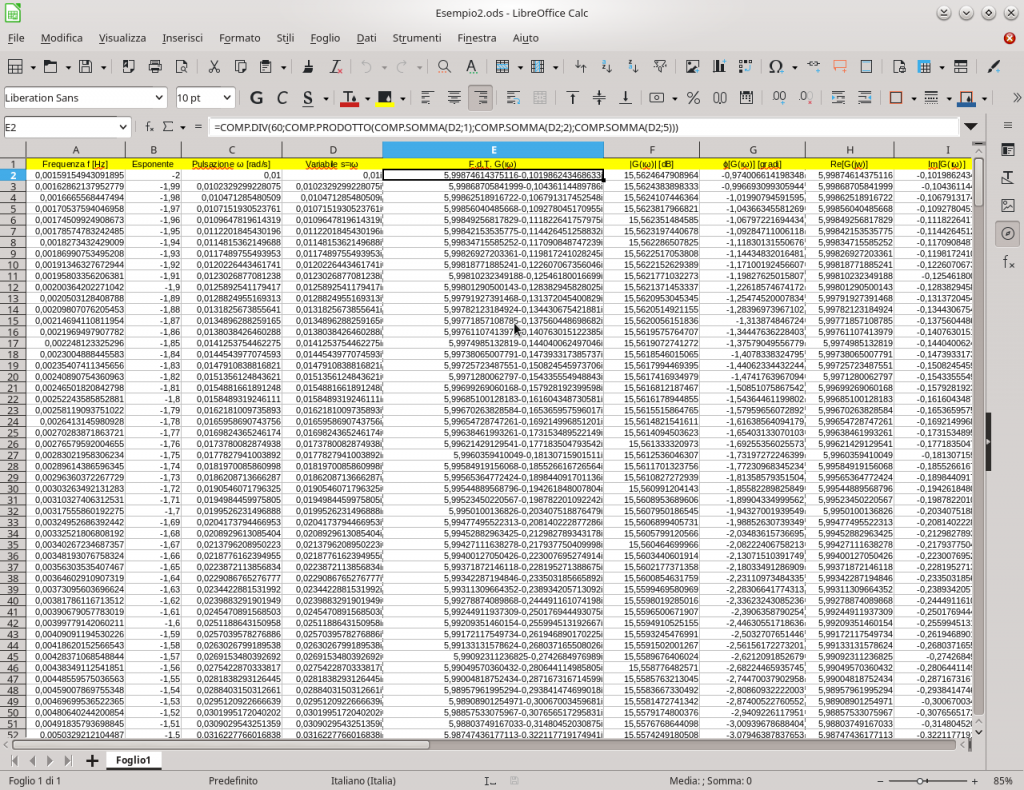
La colonna E, nello specifico relativo alla scrittura della funzione di trasferimento f.d.t, è caratterizzata dall’utilizzo combinato di tre funzioni, di preciso:

• COMP.SOMMA(Numero1;Numero2;…;Numero255) che restituisce la somma di un insieme di numeri complessi fino ad un massimo di 255;
• COMP.PRODOTTO(Numero1;Numero2;…;Numero255) la quale restituisce il prodotto di un insieme di numeri complessi, fino ad un massimo di 255;
• COMP.DIV(Num;Den) che restituisce la divisione (quoziente) di due numeri complessi.

Poiché l’obiettivo è la f.d.t.:

F(s)=\frac{1}{(s+1)(s+3)}

allora la funzione COMP.DIV() assumerà come numeratore il valore 1 e denominatore il prodotto di due numeri complessi ottenuto con la funzione COMP.PRODOTTO() caratterizzata da due argomenti, uno per ogni numero complesso e laddove il singolo argomento altro non è che l’applicazione della funzione COMP.SOMMA() dove viene sommata la parte reale e la parte immaginaria. In definitiva nella cella E2 è sufficiente inserire la seguente riga:

=COMP.DIV(1;COMP.PRODOTTO(COMP.SOMMA(D2;1);COMP.SOMMA(D2;3)))

laddove la cella D2 indica la variabile s mentre 1 e 3 sono i coefficienti reali del numero complesso. Infine attraverso la nota funzione di completamento automatico si riempiranno i valori delle rimanenti 599 celle.

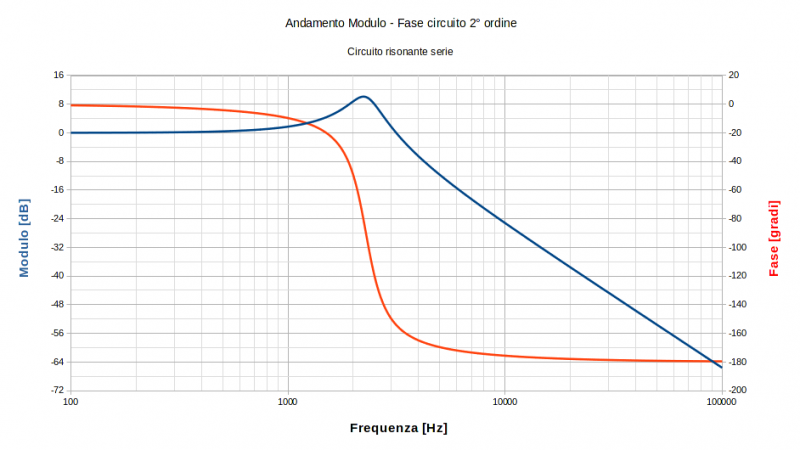
La colonna F riporta il modulo in decibel [dB] della funzione di risposta armonica. Per ottenere questo valore si valuta dapprima il modulo del numero complesso corrispondente attraverso l’uso della funzione COMP.MODULO(Numero) quindi il risultato lo si da come argomento alla definizione del decibel 20*log₁₀|Numero| ottenuto riportando la seguente riga nella cella F2:

=20*LOG10(COMP.MODULO(E2))

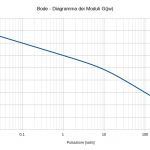
dove si è fatto uso della funzione LOG10(Numero) per valutare il logaritmo in base 10 del modulo. La moltiplicazione per 20 fornirà il risultato in dB (come da definizione) e il completamento automatico farà il resto. Da questa colonna verrà ricavato l’andamento del modulo del diagramma di Bode.

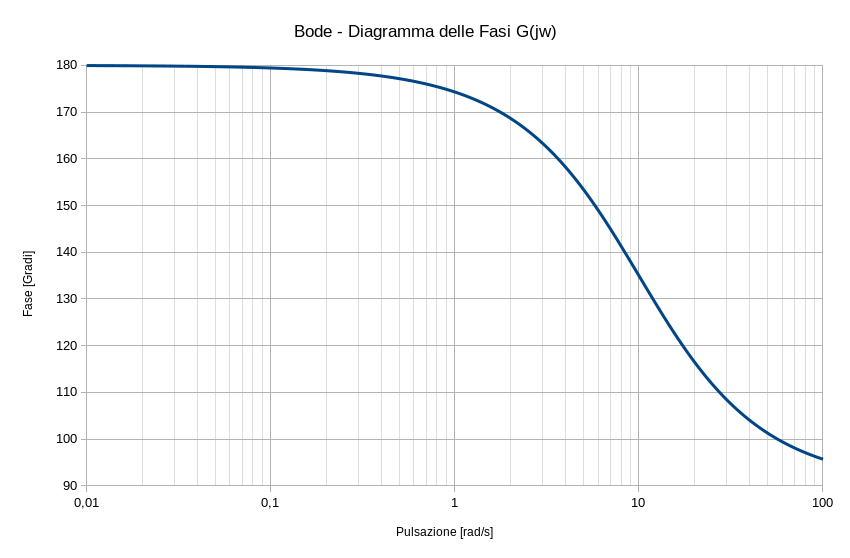
Nella colonna G viene calcolata la fase della funzione di risposta armonica al variare di s (ovvero di ω). Per ottenere il valore viene fatto uso della funzione COMP.ARGOMENTO(Numero) la quale restituisce l’argomento del numero complesso che le è stato passato, ma attenzione però, perché il valore è calcolato, quindi restituito, in radianti. A noi interessa il calcolo in gradi sessagesimali (angolo piatto 180°) pertanto il risultato della funzione va convertito moltiplicandolo dapprima per 180° quindi dividendolo per π. In definitiva nella cella G2 verrà scritto:

=COMP.ARGOMENTO(E2)*180/PI.GRECO()

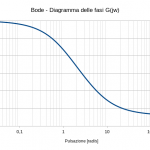
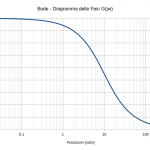
dove si è fatto uso della costante simbolica PI.GRECO() la quale restituisce il valore della costante matematica π con 14 cifre decimali dopo la virgola, di preciso 3,14159265358979. Si va di completamento e anche questa colonna è terminata. Da questa colonna verrà ricavato necessariamente l’andamento del grafico della fase del diagramma di Bode.

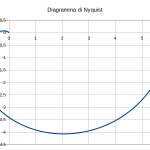
Nella colonna H e nella colonna I si divide la parte reale e la parte immaginaria del valore che assume la f.d.t al variare di s. Questa operazione viene fatta poiché per riportare l’andamento del diagramma di Nyquist occorrono i valori della parte reale e immaginaria separati. Infatti sull’asse delle ascisse verranno riportati i valori reali al variare di s, sull’asse immaginario la parte immaginaria della f.d.t al variare di s. Per separare parte reale e immaginaria vengono utilizzate rispettivamente le funzioni COMP.PARTE.REALE(Numero) e COMP.IMMAGINARIO(Numero). Infine il completamento automatico porrà fine all’inserimento dei dati dopo i quali è possibile passare alla realizzazione dei diagrammi di Bode e Nyquist per i quali è riportata l’intera procedura nel video.

Al termine è sempre possibile esportare i grafici come immagine. A tale scopo è sufficiente selezionare il grafico, cliccare con il pulsante destro del mouse e dal menù contestuale optare per Esporta come immagine. I risultati in basso.

 

Argomento numero complesso

Prima di analizzare il secondo esempio, preso nell’ordine in cui appare nell’articolo Criterio di stabilità di Nyquist, è il caso di fare alcune osservazioni/precisazioni sull’argomento di un numero complesso.

Definizione: Dato un numero complesso z non nullo si definisce argomento principale di z e lo si indica con Arg(z), quell’unico valore tra tutti i possibili argomenti di z che si trova nell’intervallo (−π, π] ovvero -π<Arg(z)≤π. In alternativa è possibile indicare l’intervallo di definizione dell’argomento di un numero complesso in [0,2π) e quindi per 0≤Arg(z)<2π.

È noto come in coordinate polare un numero, complesso in questo specifico scenario, sia possibile scriverlo:

\left \{  \begin{array}{ll} Re=r \cos\theta\\Im=r \sin\theta \end{array} \right.

il cui modulo è pari a:

|z|=\sqrt{Re^2+Im^2}

mentre per il valore della fase (argomento), positivo se in senso antiorario negativo altrimenti, si può scrivere:

\cos\theta=\frac{Re}{|z|}=\frac{Re}{\sqrt{Re^2+Im^2}}\text{ , } \sin\theta=\frac{Im}{|z|}=\frac{Im}{\sqrt{Re^2+Im^2}}

quindi, ricordando la definizione di tangente:

\tg\theta=\frac{\sin\theta}{\cos\theta}=\frac{Im}{Re}

A questo punto per il calcolo della fase si sarebbe tentati di scrivere:

\theta=\arctg\frac{Im}{Re}

che, se non contestualizzata, può condurre a risultati sbagliati! Dov’è l’errore nell’applicarla così come è scritta?

La funzione trigonometrica tangente è una funzione dispari (quindi simmetrica rispetto all’origine) di periodicità π, a valori illimitati compresi (-∞,∞) che ha per dominio di definizione l’insieme (-∞,∞) ad esclusione dei punti x=π/2+kπ con k∈Ν. Graficamente, utilizzando un tool online come GeoGebra.

 

Il browser in uso nella sessione visibile nelle immagini è Yandex. L’arcotangente (grafico a destra) è la funzione inversa della tangente e definisce l’angolo tra (-π/2,π/2) cioè il campo di valori dove la funzione tangente è invertibile e dove la tangente dell’angolo vale x, in formule:

\theta=\arctg(x) \iff x=\tg(\theta) \text{ con } \theta\isin\left(-\frac{\pi}{2},\frac{\pi}{2}\right)

e avendo ricavato che:

\theta=\arctg\frac{Im}{Re}

va da se che l’invertibilità di cui sopra avviene per valori del denominatore strettamente positivi Re>0 appartenenti quindi al primo e quarto quadrante nel quale la precedente formula vale senza errore alcuno ma solo se l’intervallo di definizione è ( − π, π]! Allora si può scrivere, in funzione dell’appartenenza al quadrante del numero complesso z:

1. Primo quadrante ovvero Re>0 e Im>0; l’argomento principale del numero z è ovviamente compreso tra (0,π/2) pertanto può essere utilizzata la formula ricavata senza errore alcuno:
   \theta=\arctg\frac{Im}{Re}
2. Secondo quadrante ovvero Re<0 e Im>0; l’argomento principale del numero z è ovviamente compreso tra (π/2,π) pertanto per far rientrare i valori nel range di invertibilità della tangente è sufficiente aggiungere π alla precedente, quindi:
   \theta=\arctg\frac{Im}{Re}+\pi
3. Terzo quadrante ovvero Re<0 e Im<0; l’argomento principale del numero z è compreso, si faccia attenzione, tra (-π,-π/2) pertanto per far rientrare i valori nel range di invertibilità della tangente è sufficiente aggiungere -π, quindi:
   \theta=\arctg\frac{Im}{Re}-\pi
4. Quarto quadrante ovvero Re>0 e Im<0; l’argomento principale del numero z è compreso tra (-π/2,0), non occorre fare nulla e rimane valida la:
   \theta=\arctg\frac{Im}{Re}

Va da se che in presenza di un numero reale positivo Arg(z)=0, se reale negativo Arg(z)=π, se immaginario positivo Arg(z)=π/2 infine se immaginario negativo Arg(z)=-π/2.

Attenzione, però, questi valori se e solo se l’intervallo di definizione dell’argomento è compreso tra (−π, π] ovvero -π<Arg(z)≤π. Cosa succede se si volesse, in alternativa, utilizzare l’intervallo di definizione dell’argomento in [0,2π) ovvero per 0≤Arg(z)<2π? Si ripete banalmente la medesima dinamica poc’anzi analizzata:

1. Primo quadrante (Re>0 e Im>0); continua a valere l’usuale formula senza la necessità di aggiungere o sottrarre alcunché:
   \theta=\arctg\frac{Im}{Re}
2. Secondo quadrante (Re<0 e Im>0); è sufficiente aggiungere π alla nota formula, quindi:
   \theta=\arctg\frac{Im}{Re}+\pi
3. Terzo quadrante (Re<0 e Im<0); in questo caso si rientra nel punto precedente pertanto è sufficiente di nuovo aggiungere π alla solita formula per ritrovare lo stesso risultato del punto 2:
   \theta=\arctg\frac{Im}{Re}+\pi
4. Quarto quadrante (Re>0 e Im<0); in quest’ultimo quadrante per rientrare nel dominio di invertibilità della tangente occorre aggiungere 2π pertanto la formula corretta diventa:
   \theta=\arctg\frac{Im}{Re}+2\pi

Infine in presenza di numeri reali positivi, numeri reali negativi, numeri immaginari positivi e numeri immaginari negativi si ha rispettivamente Arg(z)=0, secondo/terzo punto (valgono entrambi per parte reale negativa e qualsiasi valore dell’immaginario, compreso lo 0), Arg(z)=π/2 e infine Arg(z)=3π/2.

 

Esempio numero 2

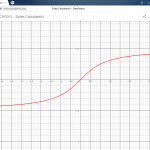
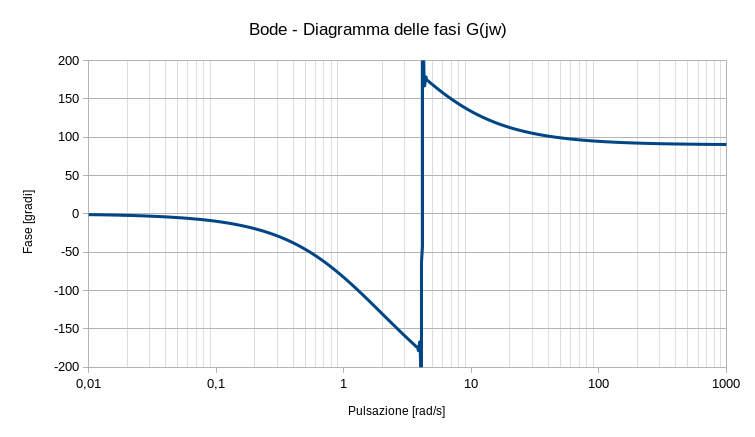
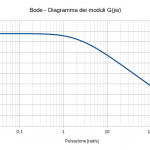
La funzione di trasferimento oggetto del secondo esempio vede la seguente forma:

F(s)=\frac{60}{(s+1)(s+2)(s+5)}

L’analisi viene condotta in un range di pulsazioni da 10^-2 rad/s a 10³ rad/s il che comporta, ipotizzando come l’esempio precedente una variazione di 1 centesimo dell’esponente, la creazione di 500 celle con valore dell’esponente da -2 a +3. La dinamica è la stessa visibile nel video.

Due i punti dove si potrebbe “inciampare”. Il primo è la corretta scrittura della funzione di trasferimento. Rispetto all’esempio precedente si ha di fatto la medesima forma solo che al denominatore risultano 3 termini a moltiplicare da inserirsi nella funzione COMP.PRODOTTO() caratterizzata, in questo caso, da tre argomenti, uno per ogni numero complesso. DI nuovo, il singolo numero complesso sarà l’applicazione della funzione COMP.SOMMA(). In sostanza la rappresentazione della f.d.t vede il seguente rigo da riportare nella cella E2 di LibreOffice Calc:

=COMP.DIV(60;COMP.PRODOTTO(COMP.SOMMA(D2;1);COMP.SOMMA(D2;2);COMP.SOMMA(D2;5)))

Il secondo punto potrebbe essere la rappresentazione della fase. Seguendo lo stesso iter del video nella cella dedicata alla fase si andrebbe ad inserire la seguente riga:

=COMP.ARGOMENTO(E2)*180/PI.GRECO()

la quale porterebbe al grafico:

poiché prende come dominio di definizione il campo di valori (−π, π] infatti si nota come superati i -180° il grafico riparta da +180° per poi ridursi fino a +90° per la presenza dell’ultimo polo al denominatore della f.d.t.

Di per se il grafico non è sbagliato, è sufficiente saperlo interpretare. È evidente infatti come avendo solo tre poli a parte reale negativa al denominatore della f.d.t., e null’altro, ci si aspetta che la fase parta da 0° per arrivare fino a -270°. E allora se si volesse rappresentare il grafico per quello che effettivamente risulta in un diagramma di Bode delle fasi ottenuto da programmi come Scilab e software simili come operare? Occorre cambiare dominio di definizione nel campo di valori [0,2π) istruendo di conseguenza LibreOffice Calc.

Per ottenere questo risultato non si utilizzerà, come fatto in “Esempio numero 1“, la funzione COMP.ARGOMENTO() ma ci si avvarrà della funzione ARCTAN.2(X,Y) la quale restituisce l’angolo, in radianti, intercorrente tra l’asse delle x (asse reale) e un segmento che collega l’origine a (X,Y) rispettivamente coordinata X e Y del punto per il quale si vuole calcolare l’angolo. Poiché occorrono le coordinate X e Y non si utilizzeranno più le celle dei valori della f.d.t come in “Esempio numero 1“, ma si farà uso della parte reale e parte immaginaria (rispettivamente colonna H e colonna I) utilizzate per la costruzione del diagramma di Nyquist.

Come usare questa nuova funzione? Se si provasse ad utilizzarla inserendo nella prima cella della fase (colonna G) la riga

=ARCTAN.2(H2;I2)*180/PI.GRECO()

non cambierebbe nulla poiché il dominio di definizione rimarrebbe sempre (−π, π] originando così lo stesso grafico. Come risolvere e dire a LibreOffice Calc di seguire un altro dominio di valori? Tramite la funzione IF(), o meglio, nella versione Italiana, la funzione SE() la quale specifica un test logico da eseguire e la cui sintassi vede:

SE(Test ; Esegui VERO ; Esegui FALSO

laddove Test è un valore/espressione qualsiasi che può dare come risultato VERO o FALSO. Per questo grafico il test è semplice e la riga da inserire nella prima cella della fase, per poi applicare il completamente automatico per tutte le altre celle, è:

=SE((ARCTAN.2(H2;I2)*180/PI.GRECO())<0; (ARCTAN.2(H2;I2)*180/PI.GRECO()); ARCTAN.2(H2;I2)*180/PI.GRECO()-360)

In buona sostanza fino a che il valore rimane negativo si lascia tutto così com’è eseguendo sempre la condizione VERO. Non appena il valore della fase diventa positivo viene eseguita la condizione FALSO applicando la stessa fase ma sottratta di 360°. Il risultato dei diagrammi del modulo e della fase unitamente al diagramma di Nyquist sono riportati di seguito, da confrontarsi con i risultati ottenuti con Scilab nel secondo esempio dell’articolo Criterio di stabilità di Nyquist.

 

 

Esempio numero 3

Per il terzo esempio la funzione di trasferimento ad anello aperto risulterà

F(s)=\frac{1}{s(s+10)}

Si è in presenza di un polo nell’origine pertanto, intuitivamente, per valori della pulsazione ω→0 è evidente come il grafico del modulo tenda ad infinito e, proprio per la presenza di un polo nell’origine, la fase partire da -90°. L’analisi prevede valori della pulsazione da 0,01 rad/s a 1.000 rad/s quindi con una variazione dell’esponente -2≤X≤3 per un totale di 500 celle (ipotizzando una variazione centesimale dell’esponente nel passare da una cella a quella immediatamente in basso/alto).

Nell’inserimento dei dati non c’è nulla di particolare né nel riportare la funzione di trasferimento, né nella fase per la quale, in questo contesto, può essere utilizzata la riga:

=(COMP.ARGOMENTO(E2)*180)/PI.GRECO()

La funzione di trasferimento, invece, può essere indicata con la seguente riga:

=COMP.DIV(1;COMP.PRODOTTO(COMP.SOMMA(D2);COMP.SOMMA(D2;10)))

nella quale l’unica particolarità è quella di indicare nella funzione COMP.SOMMA() solo la variabile s – cella D2 – essendo un polo nell’origine. Il risultato è riportato in basso:

 

Per il diagramma di Nyquist occorre sempre ricordare come manchi la parte speculare rispetto all’asse delle ascisse e inoltre, in questo contesto, la chiusura del diagramma da ω=0^– a ω=0⁺ da farsi con un numero di semigiri orari equivalenti alla molteplicità del polo, nello specifico solo 1.

 

Esempio numero 4

Per questo esempio la funzione di trasferimento vede un polo doppio nell’origine:

F(s)=\frac{1}{s^2(s+10)}

La procedura riamane del tutto identica agli esempi già visti. L’analisi vede la pulsazione in un campo compreso da 0,01 rad/s a 100 rad/s quindi per l’esponente una variazione da -2≤X≤2 per un totale di 400 celle a variazione 1 centesimo l’una dall’altra.

Per passare a LibreOffice Calc la funzione di trasferimento in questo caso occorre tenere in conto che il numero complesso s dovrà essere elevato al quadrato. Ciò lo si può fare utilizzando l’apposita funzione COMP.POTENZA(Numero;Potenza) che da come risultato il numero complesso Numero elevato al valore Potenza. Se lo si vuole verificare a mano si ricorda che la potenza di un numero complesso altro non è che l’applicazione della formula di De Moivre con il numero complesso rappresentato in forma trigonometrica. In definitiva la riga da inserire è:

=COMP.DIV(1;COMP.PRODOTTO(COMP.POTENZA(D2;2);COMP.SOMMA(D2;10)))

Per la fase il “grafico reale” parte da -180° a causa del doppio polo nell’origine per scendere a -270° a causa della presenza dell’altro polo a parte reale negativa. Utilizzando la solita riga:

=(COMP.ARGOMENTO(E2)*180)/PI.GRECO()

il grafico partirebbe però da +180° per i motivi già addotti, cioè:

 

Naturalmente non è sbagliato, ma volendo ottenere il grafico così come ci si aspetterebbe allora di nuovo occorre “istruire” LIbreOffice Calc a cambiare il comportamento predefinito. La riga da inserire è abbastanza semplice, non c’è nessuna condizione da verificare ed è sufficiente la:

=ARCTAN.2(H2;I2)*180/PI.GRECO()-360

Il risultato è riportato nel seguito per tutti e tre i diagrammi.

 

Anche in questo caso per il diagramma di Nyquist manca la parte speculare (rivolta verso il basso) per valori della pulsazione da ω=-∞ a ω=0^– e la chiusura del diagramma in questo caso da farsi con due mezzi giri in senso orario poiché la molteplicità del polo è pari a 2.

 

Esempio numero 5

[in preparazione]