Elementi in parallelo: resistenze
In un circuito elettrico non è raro trovare elementi in parallelo. Due o più elementi si definiscono in parallelo quando sottoposti alla stessa differenza di potenziale (d.d.p.). In un circuito elettrico possono essere in parallelo sia elementi attivi (e.g. generatori di tensione) sia elementi passivi.
Indice - Table of Contents
Calcolo resistenza equivalente
In questo contesto verranno trattati elementi passivi in parallelo e di preciso delle resistenze.
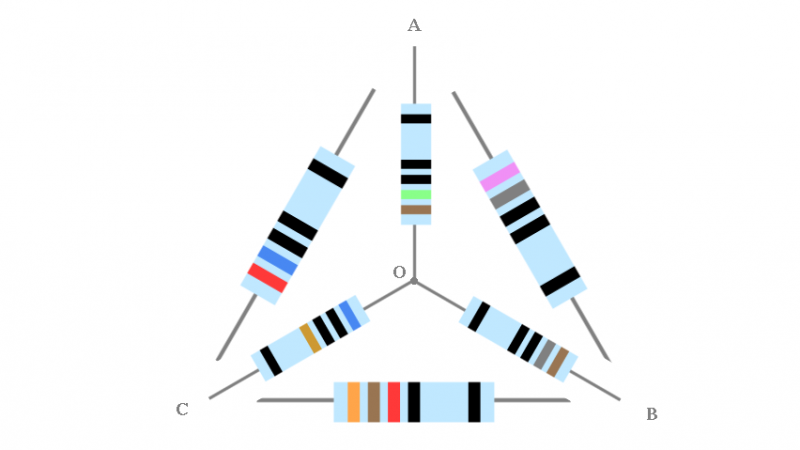
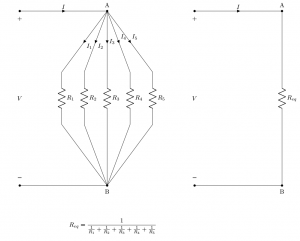 Si considerino più resistori in parallelo, 5 per semplicità nella figura di lato (un click per ingrandirla), ma il numero non lede la generalità della discussione e relativa dimostrazione riportata in basso. Della figura in questione gli interessati potranno trovare lo snippet in TeX-LaTeX al seguente indirizzo.
Si considerino più resistori in parallelo, 5 per semplicità nella figura di lato (un click per ingrandirla), ma il numero non lede la generalità della discussione e relativa dimostrazione riportata in basso. Della figura in questione gli interessati potranno trovare lo snippet in TeX-LaTeX al seguente indirizzo.
L’obiettivo in questa sede è dimostrare la formula per resistori in parallelo e riportarne il caso particolare – tipicamente il più utilizzato – per due sole resistenze in parallelo.
Con riferimento alla figura, applicando la prima Legge di Kirchhoff al nodo A, risulta:
I=I_1+I_2+I_3+I_4+I_5\kern{1cm}(1)
Ora dalla 1^a Legge di Ohm su ogni singolo resistore è possibile scrivere:
I_1=\frac{V}{R_1}; I_2=\frac{V}{R_2}; I_3=\frac{V}{R_3}; I_4=\frac{V}{R_4}; I_5=\frac{V}{R_5}\kern{1cm}(2)
Sostituendo le (2) nella (1) risulta:
I=\frac{V}{R_1}+\frac{V}{R_2}+\frac{V}{R_3}+\frac{V}{R_4}+\frac{V}{R_5}
nella quale mettendo in evidenza la tensione V risulta:
I=V\left(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4}+\frac{1}{R_5}\right)\kern{1cm}(3)
Ponendo:
\frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4}+\frac{1}{R_5}
allora dalla (3) è evidente come la corrente assorbita dal gruppo di resistenze sia pari a:
I=\frac{V}{R_{eq}}
ovvero:
R_{eq}=\frac{V}{I}\kern{1cm}(4)
Ma dalla (3) si ricava:
\frac{V}{I}=\frac{1}{(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R_4}+\frac{1}{R_5})}
che sostituita nella (4) porta alla formula finale:
R_{eq}=\frac{1}{(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\frac{1}{R4}+\frac{1}{R_5})}\kern{1cm}(5)
ovvero alla forma generale:
R_{eq}=\frac{1}{(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\dots+\frac{1}{R_{n-1}}+\frac{1}{R_n})}\kern{1cm}(5)
Caso particolare: due resistenze in parallelo
Nel caso di due soli resistori la (5) può essere riscritta come:
R_{eq}=\frac{1}{(\frac{1}{R1}+\frac{1}{R2})}
Il minimo comune multiplo a denominatore porta a:
R_{eq}=\frac{1}{(\frac{R_2 + R_1}{R_1*R_2})}
ovvero:
R_{eq}=\frac{R_1 * R_2}{R_1 + R_2}
Un esempio
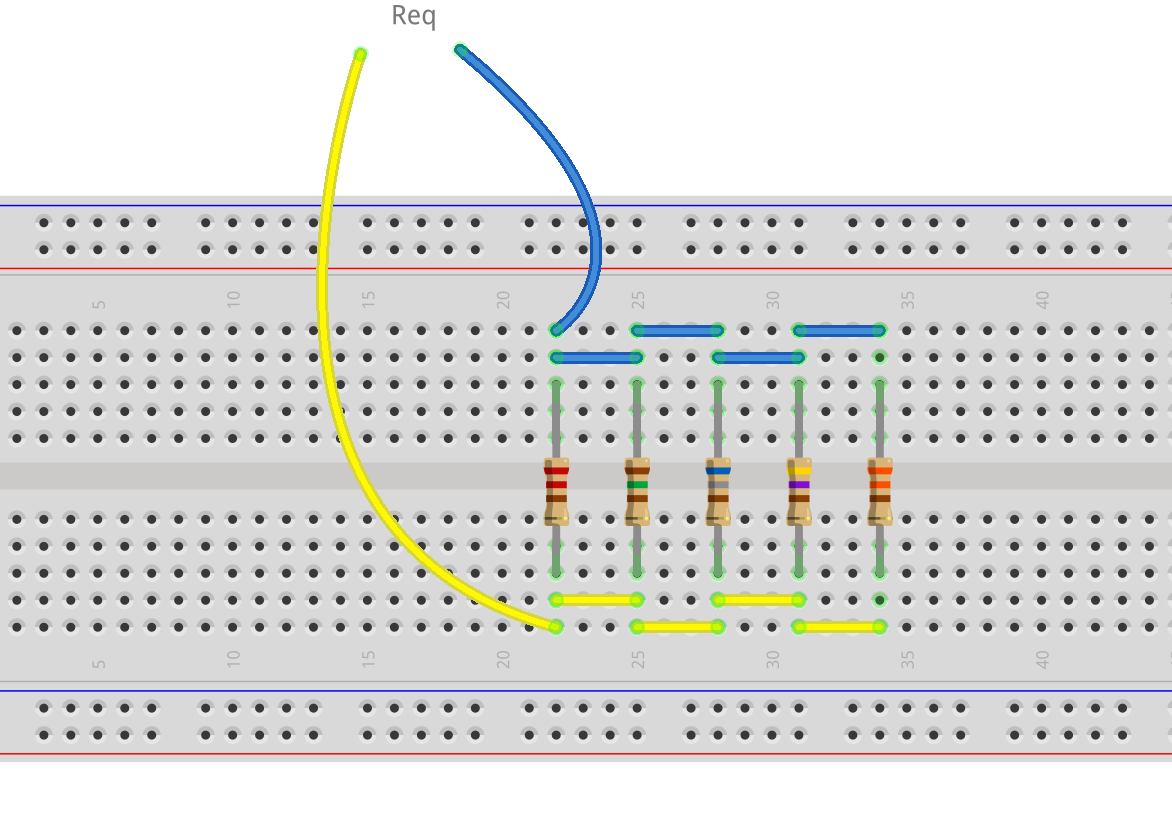
Con riferimento alla figura di apertura si può notare come sulla breadboard virtuale siano state collegate 5 resistenze in parallelo di valore, rispettivamente da sinistra verso destra, 220\Omega, 150\Omega, 680\Omega, 470\Omega e 330\Omega.
Applicando la formula (5) è possibile conoscerne il valore equivalente R_{eq} ai capi dei fili giallo e blu:
R_{eq}=\frac{1}{(\frac{1}{220}+\frac{1}{150}+\frac{1}{680}+\frac{1}{470}+\frac{1}{330})}\approx 56\Omega
[url=https://sviloguzov.ru/kru]реклоузер 6 кв[/url]
Thank you for an effectively composed conversation message and anticipating proceed collaborating with this professional task was excellent would refer anyone to utilize you all when it involves assiting with task it was great yet had some misconception as well as not clear for the tutor however I tried. and got [url=https://codingforstudent.com/]Coding for Student [/url] somehow great marks
Hi there fantastic website! Does running a blog such as this require a lot of work? I have absolutely no understanding of programming but I was hoping to start my own blog in the near future. Anyways, should you have any suggestions or tips for new blog owners please share. I understand this is off topic however I just wanted to ask. Cheers!
What do you think about this information? https://arsmash.ru/
I think it is good!!!
Great post
[url=https://brianclarkelectricalservices.co.uk][img]https://brianclarkelectricalservices.co.uk/wp-content/uploads/2021/09/technological-progress.jpg[/img] [/url]
In many areas, becoming a [url=https://brianclarkelectricalservices.co.uk/ [b]Certified Electrician UK [/b] [/url] through a formal apprenticeship program is the most effective way to learn electrician skills and gain the necessary experience to land high-paying jobs.
Most apprentice electricians complete their apprenticeship in just two years. Some apprentices get more training and experience than others, though, and some people who take advantage of a certified electrician apprenticeship program find that their job skills improve a great deal after their apprenticeship is finished.
[url=https://brianclarkelectricalservices.co.uk
]Electrician London
[/url]
Thank you, I have just been looking for information approximately this topic
for a wbile and yours is thee greatest I have found out sso
far. However, what concerning the conclusion? Are you sure abouit tthe supply?
My blog … module exams (https://examenhome.com/)
Интернет-магазин Alpenbox — распределительные устройства и удлинители от производителя. Доставка по Москве и всей России