Introduzione

Un interessante fenomeno, al quale poi venne associato un omonimo teorema, venne spiegato prima e formulato in seguito alla fine della seconda decade del millennio scorso.

L’effetto dovrà essere gioco forza applicato in diversi contesti se si vuole tenere debitamente in conto di tutti i parametri che intervengono in determinate condizioni sia esso un circuito elettrotecnico e/o elettronico come avrò modo di illustrare in successivi articoli (e.g. influenza frequenza di taglio superiore di amplificatori audio, modifica risposta circuiti in alta frequenza fino alle perdite di commutazione in alimentatori SMPS, Switch Mode Power Supply). In altri contesti l’effetto Miller è voluto e amplificato al fine di migliorare la risposta in frequenza, tale tecnica è definita come compensazione di Miller o Pole-splitting.

 

Un po’ di storia

Correva l’anno 1919 quando l’ingegnere elettrico statunitense John Milton Miller si trovò davanti ad un dilemma mai risolto fino a quel momento. Occorre ricordare che all’epoca i BJT (Bipolar Junction Transistor) non esistevano e l’effetto di campo (precursore dei FET – Field Effect Transistor) veniva osservato solo diversi anni dopo (1925).

Si avevano a disposizione solo i tubi a vuoto, o valvole termoioniche, che basavano il proprio funzionamento sull’omonimo effetto, l’effetto termoionico (o termoelettrico che dir si voglia).

Nello specifico i dispositivi con i quali Miller si trovava a lavorare erano i triodi a vuoto, valvole caratterizzate da tre elettrodi: un catodo il quale per effetto termoionico, una volta riscaldato (in maniera diretta o indiretta), emette elettroni, un anodo che raccoglie l’emissione del catodo se il suo potenziale è superiore al catodo e infine una griglia la cui funzione è quella di regolare, in rapporto al proprio potenziale, il numero (la quantità) di elettroni che dal catodo possono raggiungere l’anodo.

Il principio di funzionamento è piuttosto intuitivo. Lo ricordo molto brevemente e a grandi linee: se la griglia ha un potenziale sufficientemente negativo respinge gli elettroni prodotti dal catodo e in questo scenario non vi è alcuna corrente tra catodo e anodo. L’aumento progressivo del potenziale di griglia da un valore negativo verso lo 0, fa uscire il triodo dalla condizione di interdizione (cutoff) incrementando così la corrente che scorre in esso.

L’uso dei triodi vedeva – e vede ancora oggi – applicazioni in bassa frequenza per amplificatori audio generalmente (ma non esclusivamente) in ambito musicale, così come l’uso in alta frequenza (trasmettitori radio e TV) fino alle applicazioni industriali, ad esempio nel riscaldamento e/o incollaggio plastiche in alta frequenza generalmente intorno ai 30MHz e nelle saldatrici industriali come tubi di oscillazione per potenze da qualche kW fino ad oltre i 20kW. All’epoca venivano utilizzati anche per realizzare degli oscillatori locali.

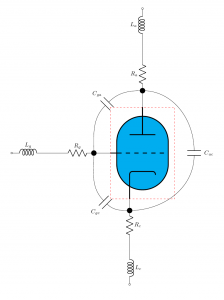
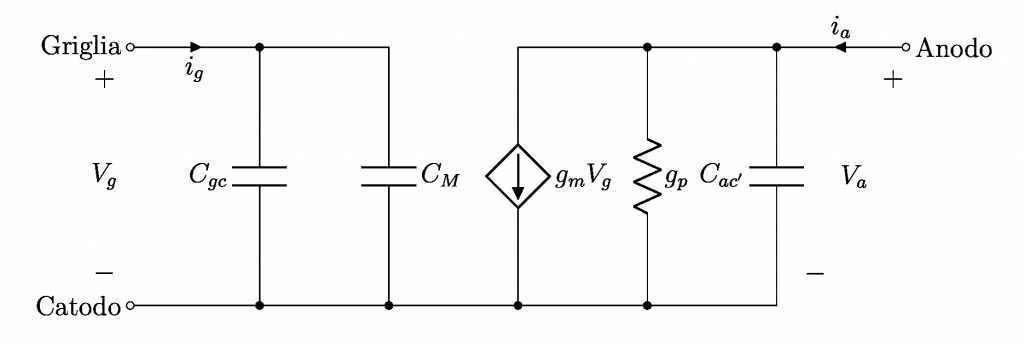
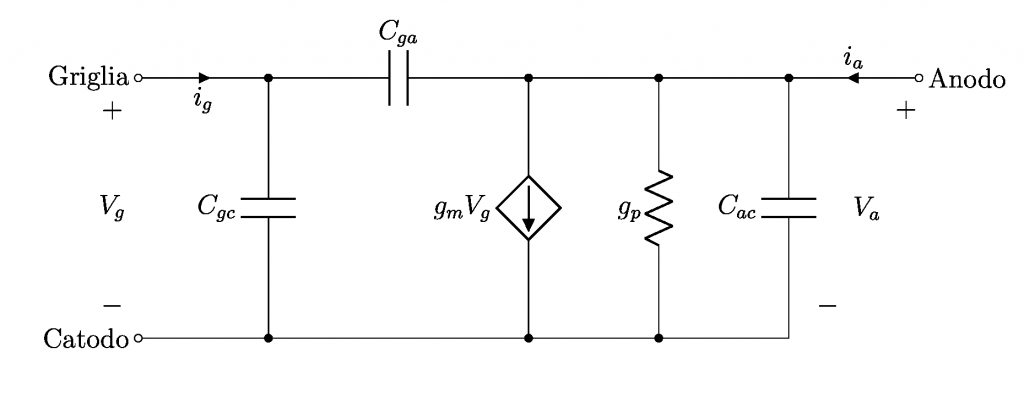
Arrivando al nocciolo della questione nella figura a lato è riportato il circuito equivalente di un triodo (nel riquadro rosso il triodo ideale): l’immagine è ottenuta utilizzando TeX-LaTeX e, gli interessati, possono prendere lo snippet nel breve report nella sezione TeX-LaTeX dedicata: Triodo: disegnarne il circuito equivalente.

La capacità “vista” in ingresso determina il taglio alle alte frequenze ovvero concorre nel valore della frequenza di taglio superiore. Osservando lo schema equivalente dei componenti sui quali si trovava a lavorare l’ingegner Miller, è possibile subito affermare che, per quanto ne attiene la componente di segnale, di fatto, trascurando gli elementi parassiti resistivi e induttivi, possiamo considerare 2 capacità in parallelo: allora senza aggiungere alcun’altra informazione la capacità totale vista dall’ingresso è data dalla somma della Cgc (ipotizzando il catodo a massa) sommata alla Cga (considerando la resistenza di carico di valore trascurabile). Il valore di tale somma è tipicamente dell’ordine di qualche picofarad com’è possibile verificare dai datasheet dei triodi di uso comune, ad esempio il doppio triodo 12AX7 riportato in basso.

12ax7

---

Quanto riportato è ciò che effettivamente risultava anche all’ingegner Miller durante le sue misure aspettandosi così una frequenza di taglio superiore congruente con i valori misurati.

In realtà le prove in frequenza suggerivano la mancanza di un qualche elemento alla discussione perché veniva rilevata una frequenza di taglio superiore più bassa di quella attesa, significativa di una capacità di ingresso superiore rispetto a quella misurata!

Era un comportamento noto da tutti gli altri sperimentatori ma nessuno fino a quel momento aveva dato una corretta spiegazione del fenomeno che arrivò solo grazie all’ingegner Miller il quale si trovava a dover studiare questo tipo di circuito equivalente (già ricavato in un precedente post Triodo: circuito equivalente):

 

Il teorema di Miller

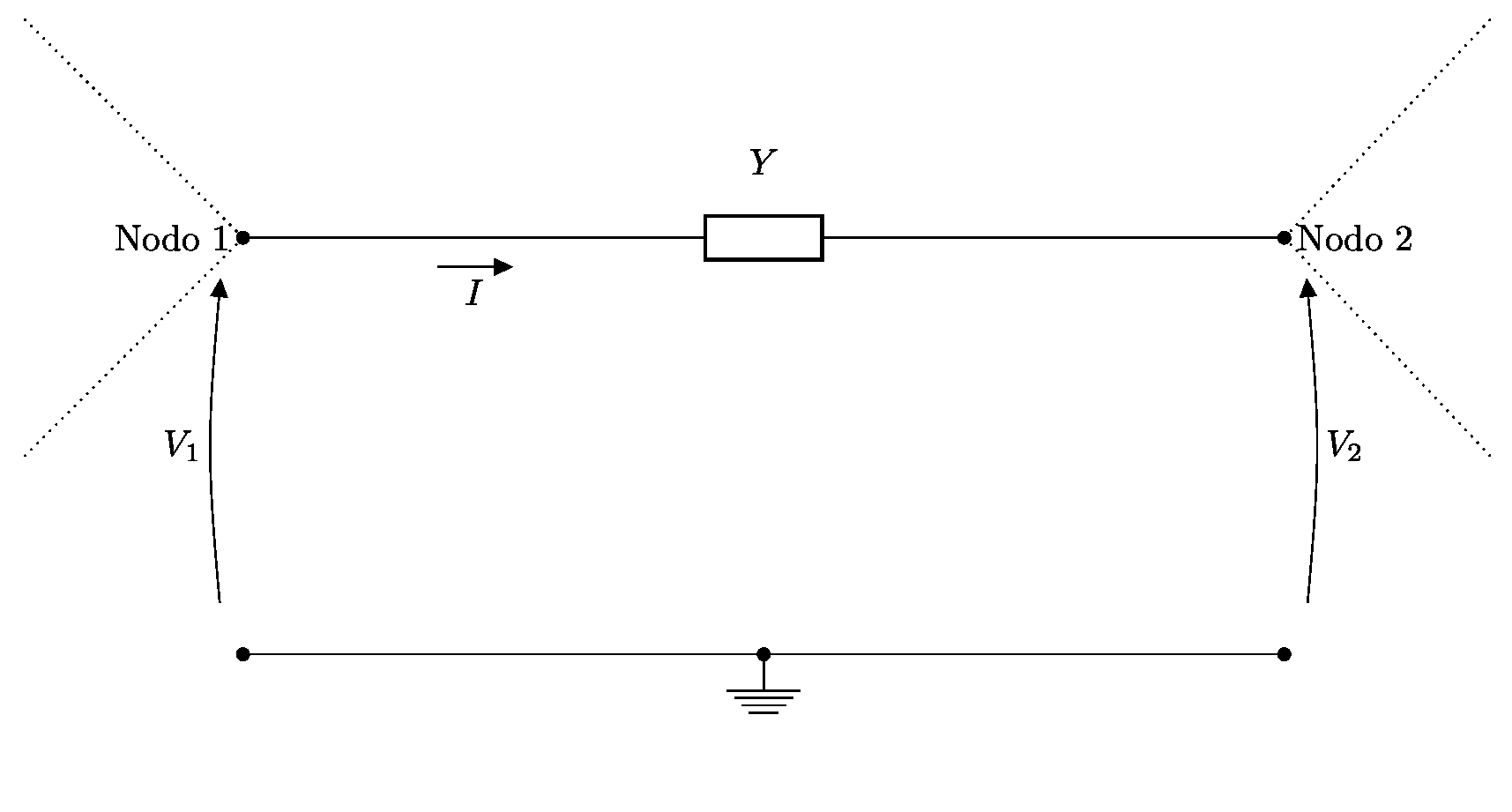
Per comprenderlo e dimostrarlo matematicamente prendiamo in considerazione una situazione assolutamente generica ma che possa ricondursi all’immagine precedente: ad esempio una parte di rete nella quale due dei suoi nodi sono collegati direttamente attraverso una ammettenza Y.

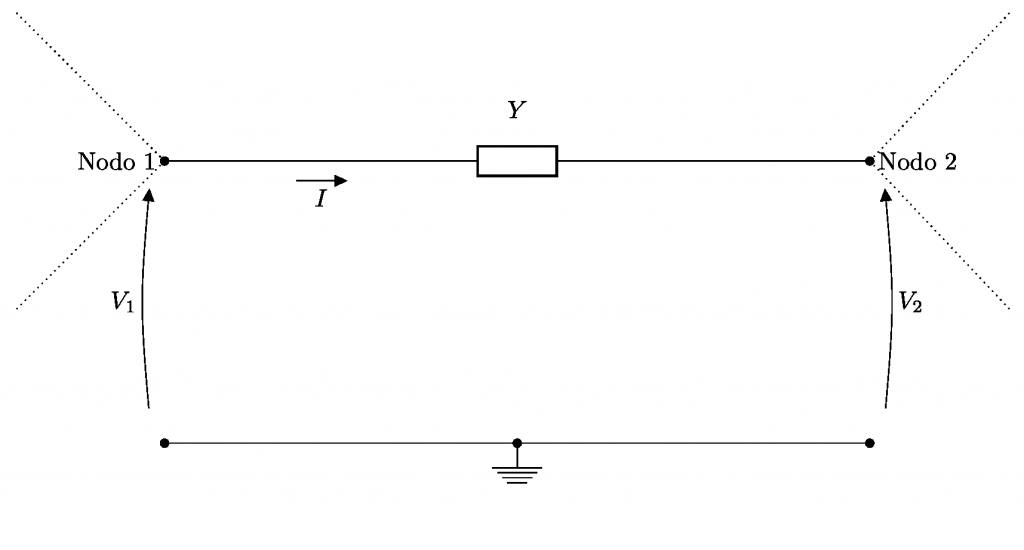
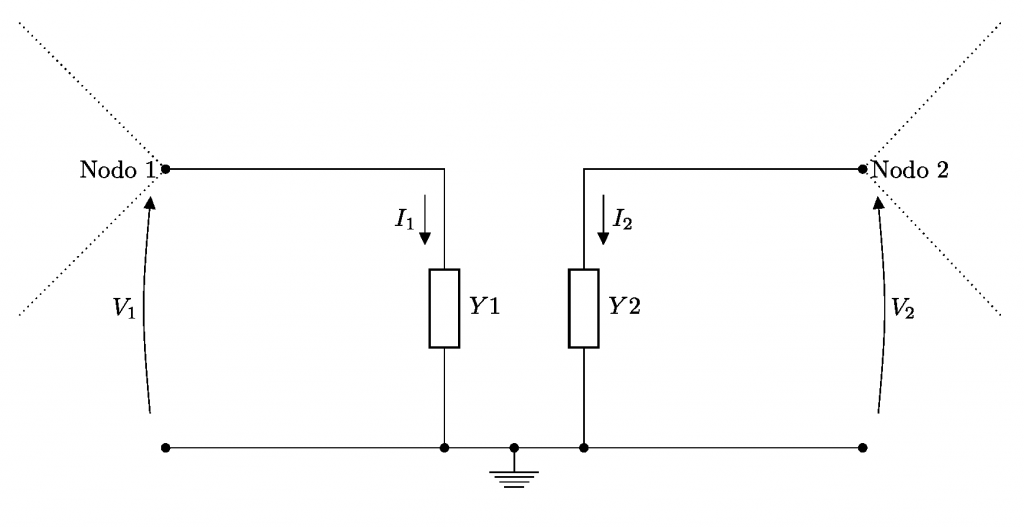
Il teorema di Miller intende fornire una formulazione tramite la quale è possibile sostituire l’ammettenza Y con una coppia di ammettenze equivalenti poste rispettivamente tra il Nodo 1 e massa e il Nodo 2 e massa, in sostanza da una ammettenza flottante di feedback a due ammettenze collegate a massa:

Il teorema si regge sulla conoscenza dei valori V_2 e V_1 il cui rapporto è definito guadagno di tensione indicato con:

A_v=\frac{V_2}{V_1}\kern{1cm}(1)

Applicando la seconda legge di Kirchhoff alla maglia visibile in Figura 3, risulta:

V_1-\frac{I}{Y}-V_2=0

pertanto la corrente I vale:

I=Y\times(V_1-V_2)\kern{1cm}(2)

Affinché nel Nodo 1 non venga percepita alcuna differenza tra la rete di Figura 3 e la rete di Figura 4 occorre che la corrente nell’ammettenza Y1 sia proprio I, cioè:

I_1=Y_1 \times V_1=I\kern{1cm}(3)

Medesimo ragionamento per il Nodo 2: affinché nel Nodo 2 non venga percepita alcuna differenza tra la topologia di Figura 3 e la topologia di Figura 4 occorre che:

I_2=-Y_2 \times V_2=I\kern{1cm}(4)

Solo così le due reti sono equivalenti. Il segno meno è dovuto al fatto che la corrente percorre l’ammettenza in senso inverso rispetto alla ddp presente nel Nodo 1 …è solo una convezione. Ora, ricordando la definizione (1), dalla (2) e per la (3), si può scrivere:

\begin{aligned}Y_1&=\frac{I}{V_1}=\frac{Y\times(V_1-V_2)}{V_1}=\\&=Y\times\left(1-\frac{V_2}{V_1} \right)=\\&=Y\times(1-A_v)\kern{1cm}(5)\end{aligned}

Analogamente, sempre dalla definizione (1), dalla (2) e per la (4), si può scrivere:

\begin{aligned}Y_2&=\frac{I}{V_2}=\frac{Y\times(V_1-V_2)}{V_2}=\\&=Y\times\left(1-\frac{V_1}{V_2}\right)=\\&=Y\times\left(1-\frac{1}{A_v}\right)\kern{1cm}(6)\end{aligned}

La (5) e la (6) definiscono le ammettenze di maglia equivalenti secondo il teorema di Miller.

A questo punto è possibile applicare il risultato del teorema di Miller per spiegare in cosa consiste e come si manifesta l’effetto Miller. Si osservi il circuito equivalente del Triodo riportato in Figura 2. La tensione V_g applicata all’ingresso fa scorrere corrente nelle due capacità C_{gc} e C_{ga} il cui calcolo è riportato nel seguito:

\begin{cases}I_{gc}=Y_{C_{gc}}\times V_{gc}\\I_{ga}=Y_{C_{ga}}\times (V_g-V_a) \end{cases}

ed è proprio la corrente I_{ga} la chiave di tutto il discorso. Esplicitandone l’ammettenza capacitiva, ricordando che l’ammettenza Y è l’inverso dell’impedenza Z e poiché Z_c=\frac{1}{\jmath{\omega}C}, la corrente I_{ga} si può scrivere come:

\begin{aligned}I_{ga}&=\jmath{\omega}C_{ga}\times (V_g-V_a)=\\&=\jmath{\omega}C_{ga}\times V_g(1-\frac{V_a}{V_g})=\\&=\jmath{\omega}C_{ga}\times V_g(1-A_v)\end{aligned}

Ponendo:

C_M=C_{ga}\times(1-A_v)\kern{1cm}(7)

la corrente I_{ga} può essere riscritta come:

I_{ga}=\jmath{\omega}C_M\times V_g

e laddove il valore di C_M espresso dalla (7) prende il nome di capacità equivalente di Miller o effetto Miller la quale, come si vede, è funzione della capacità interelettrodica intrinseca tra griglia e anodo e del valore del guadagno di tensione A_v. In tale scenario il circuito equivalente di Figura 2, dopo aver applicato il teorema di Miller, diventa:

dove il valore del condensatore in uscita C_{ac'} tiene conto dell’applicazione del teorema di Miller, di fatto due capacità in parallelo il cui valore è la somma di entrambe. Ma dalla (6) è subito visto che per valori di |A_v|\geq10 la capacità di Miller in uscita si riduce praticamente al valore della capacità ingresso-uscita sulla quale si sta applicando il teorema di Miller quindi ha poca o nulla influenza sulla frequenza di taglio inferiore nell’analisi in frequenza del sistema.

 

Effetto Miller

Diversa è la questione per la capacità C_M. Infatti ipotizzando di avere un amplificatore a catodo comune (con riferimento ad un triodo, ma il discorso non cambia se si prende in considerazione un emettitore comune per i BJT o un source comune per i MOSFET/FET) il cui guadagno di tensione sia pari a -49 è evidente come dalla (7) risulti C_M=50\times C_{ga} e allora l’effettiva capacità di ingresso del triodo è data dalla somma delle capacità in parallelo nelle quali sostituendo i valori che si possono trovare in un qualsiasi datahseet – ad esempio per la 12AX7 sopra riportato – risulta:

\begin{aligned}C_{in}&=C_{gc}+50\times C_{ga}=\\&=1,6+50\times 1,7=86,6pF\end{aligned}

Ovvero una capacità di ingresso più alta e maggiorata di un fattore proporzionale ad A_v la quale, oltre a ridurre la banda passante dell’amplificatore che si sta analizzando, ha anche una diretta conseguenza di un possibile (pre)amplificatore posto a monte il quale risulta più lento poiché soffrirà di un’alta capacità di carico posta sulla sua uscita dovuta, appunto, all’effetto Miller (capacità di feedback ingresso/uscita moltiplicata per il guadagno di tensione). E su questo non si può fare nulla a meno di adottare specifiche modalità costruttive (i.e. Tetrodi e Pentodi nel caso dei tubi a vuoto) e/o configurazioni circuitali (e.g. Cascode) che mitigano l’effetto Miller aumentando così la banda passante e facendo vedere ad un eventuale amplificatore a monte una capacità più bassa.

NOTA: è stato riportato un valore negativo del guadagno di tensione, ad esempio per gli amplificatori invertenti. E se il guadagno è positivo (amplificatori non invertenti)? Si realizza un sistema a capacità negativa! È un bene? È un male? Dipende dall’applicazione: un sistema a capacità negativa è tipicamente utilizzato alle alte frequenze per aumentare la banda passante e ridurre le perdite di potenza.

Al termine di questa trattazione si vogliono riportare alcune limitazioni del Teorema di Miller dal punto di vista statico e delle variazioni alla rete nello studio in frequenza sulle quali occorre fare un po’ di attenzione. Solo per citarle, poiché esulano dal contesto di definizione e dimostrazione del teorema e dell’effetto Miller:

• I circuiti equivalenti di Figura 3 e 4 sono tra di loro equivalenti solo se le condizioni in base alle quali si è calcolato il valore di A_v nel frattempo non sono cambiate. Ad esempio non è possibile applicare il teorema di Miller per determinare l’impedenza d’uscita poiché per il suo calcolo, convenzionalmente, occorre rimuovere il generatore d’ingresso e applicare un generatore di tensione in uscita cambiando così il valore di A_v.
• Nell’analisi in frequenza di alcune configurazioni circuitali (e.g. emettitore comune, source comune, catodo comune ecc) nell’applicare il teorema di Miller – ovvero l’approssimazione di Miller nel considerare valido e fissato il valore di A_v – passando così da una singola capacità floating/feedback a due capacità a massa, il sistema può passare da 1 polo alla presenza di 2 poli.
• Con riferimento al punto precedente il circuito originale consta, nello studio in frequenza, di uno zero ma dopo l’applicazione del teorema di Miller non c’è più alcun zero da considerare!

Gli ultimi 2 punti sono dovuti essenzialmente all’approssimazione di Miller che consiste nel considerare fissato il valore di A_v quando in realtà andrebbe valutato ad ogni cambio di frequenza. Operando con l’approssimazione di Miller in genere si commette un errore sempre più che trascurabile almeno fino a quando non si raggiungono determinati valori (alti) di frequenza. Ma questi sono altri discorsi che si vedrà di affrontare in altri articoli.