Onda trapezoidale: calcolo valore efficace e valore medio

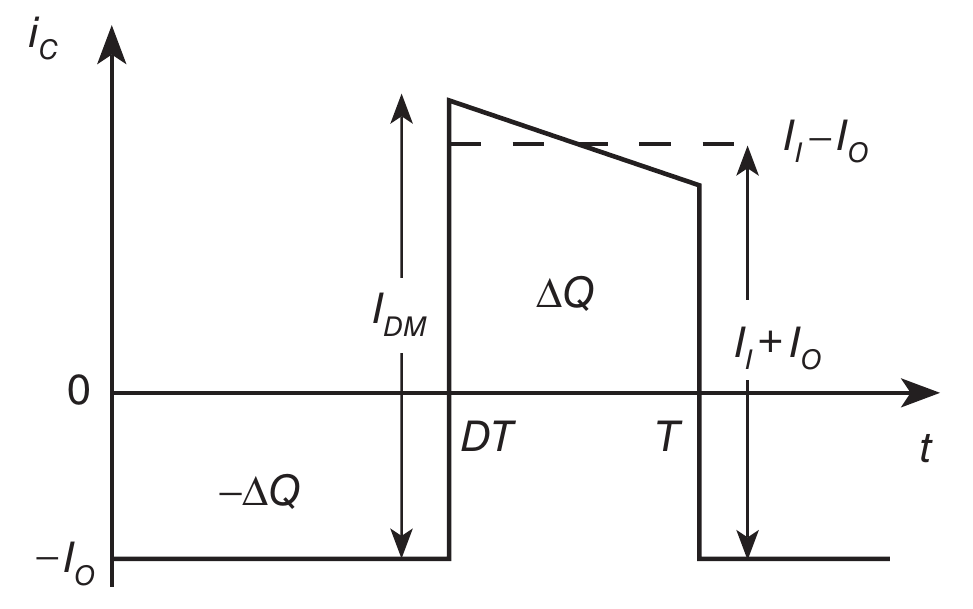
Sotto determinate condizioni di funzionamento – si pensi ad esempio all’andamento della corrente assorbita dal condensatore di uscita di un boost/step-up converter funzionante in modalità CCM (Continuous Conduction Mode) – può risultare utile la conoscenza del valore efficace e del valore medio di una forma d’onda trapezoidale periodica.

Calcolo del valore efficace

La procedura non è complicata è solo un po’ noiosa a causa di un certo numero di passaggi algebrici. Il punto di partenza vede la definizione del valore efficace come la radice della media dei quadrati (ovvero valore quadratico medio o valore RMS acronimo inglese di Root Mean Square), in formule:

F_{RMS}=\sqrt{\frac{1}{T} \int_0^T [f(t)]^2 dt}

 

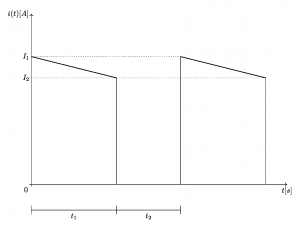
Se la funzione f(t) per la quale vogliamo calcolarne il valore RMS è ad esempio l’andamento della corrente riportata nell’immagine a lato, come primo passo occorre ricavare l’equazione della corrente tra i punti:

\left \{  \begin{array}{ll}P_1=(0,I_1)\\P_2=(t_1,I_2) \end{array} \right.

È  possibile “scomodare” l’equazione di una retta passante per due punti:

\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}

che applicata ai due punti in questione porta a:

\frac{t}{t_1}=\frac{i(t)-I_1}{I_2-I_1}

Con semplici passaggi:

\boxed{i(t)=I_1+\frac{I_2t}{t_1}-\frac{I_1t}{t_1}}

Per il calcolo del valore efficace occorre il quadrato del valore ottenuto:

[i(t)]^2=\left[I_1+I_2\frac{t}{t_1}-I_1\frac{t}{t_1}\right]^2

Da osservare che t_1 in un boost converter coincide con il t_{off} del diodo di uscita e quindi con t_{on} dello switch. Sviluppando il quadrato del trinomio:

I_1^2+I_2^2\frac{t^2}{t_1^2}+I_1^2\frac{t^2}{t_1^2}+\\[1.5em]+2 I_1 I_2\frac{t}{t_1}-2 I_1^2\frac{t}{t_1}-2 I_1 I_2\frac{t^2}{{t_1}^2}

Ma ogni singolo addendo/termine è posto in realtà sotto un segno di integrale:

\int_0^{t_1} I_1^2 \,dt +\int_0^{t_1} I_2^2\frac{t^2}{t_1^2} \,dt +\\[1.5em]\int_0^{t_1} I_1^2\frac{t^2}{t_1^2} \,dt +\int_0^{t_1} I_1^2\frac{t^2}{t_1^2} \,dt +\\[1.5em]-\int_0^{t_1} 2I_1^2\frac{t}{t_1} \,dt -\int_0^{t_1} 2I_1I_2\frac{t^2}{t_1^2} \,dt

Sviluppando ogni singolo termine:

I_1^2t_1+\frac{I_2^2}{3}\frac{t_1^3}{t_1^2}+\\[1.5em]\frac{I_1^2}{3}\frac{t_1^3}{t_1^2}+\frac{2I_1I_2}{2}\frac{t_1^2}{t_1}+\\[1.5em]-\frac{2I_1^2}{2}\frac{t_1^2}{t_1}-\frac{2I_1I_2}{3}\frac{t_1^3}{t_1^2}

che dopo semplificazione porta a:

I_1^2t_1+\frac{I_2^2}{3}t_1+\frac{I_1^2}{3}t_1+\\[1.5em]+I_1I_2t_1-I_1^2t_1-\frac{2I_1I_2}{3}t_1

ovvero:

\frac{I_1^2}{3}t_1+\frac{I_2^2}{3}t_1+\frac{I_1I_2}{3}t_1

A questo punto occorre ricordare che il suddetto sviluppo è all’interno di \sqrt\frac{1}{T} pertanto il risultato finale vede, osservando che T=t_1+t_2:

\boxed{I_{RMS}=\sqrt{(I_1^2+I_2^2+I_1I_2)\frac{1}{3}\frac{t_1}{t_1+t_2}}}

Calcolo del valore medio

Per definizione il valore medio (avg, contrazione di average in inglese) di una funzione altro non è che:

F_{avg}=\frac{1}{T} \int_0^T f(t) dt

Sostituendo sotto il segno di integrale la i(t) precedentemente calcolata in luogo della f(t) e sviluppando risulta:

I_{avg}=\frac{1}{T} \int_0^T i(t)dt=\frac{1}{T} \int_0^{t_1}I_1 dt+\\[1.5em]+\frac{1}{T} \int_0^{t_1} \frac{I_2t}{t_1}dt-\frac{1}{T} \int_0^{t_1} \frac{I_1t}{t_1} dt

mettendo in evidenza \frac{1}{T} e sviluppando ogni singolo integrale risulta:

I_{avg}=\frac{1}{T}\left[I_1t_1+\frac{I_2t_1^2}{2t_1}-\frac{I_1t_1^2}{2t_1}\right]

e in definitiva il valore medio cercato:

\boxed{I_{avg}=\frac{1}{2}\frac{t_1}{t_1+t_2}(I_1+I_2)}

È noto come il valore efficace, a meno di avere una grandezza costante (i.e. indipendente dal tempo), è sempre maggiore del valore medio: F_{RMS}>F_{avg}.

NOTA: L’immagine presa come riferimento per l’andamento della corrente è stata ottenuta utilizzando il pacchetto TikZ in LaTeX. Gli interessati possono usufruire dello snippet per i loro usi al seguente indirizzo.