Trasformazioni Triangolo-Stella e Stella-Triangolo di resistenze

Diversi possono essere i modi di collegamento di tre resistenze; ad esempio in parallelo, in serie o un “misto” di serie e parallelo (e.g. due in serie con il terzo in parallelo alla serie oppure due in parallelo con in serie il terzo bipolo).

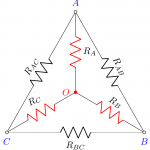Molto interessante, in questo contesto, altre due tipologie di collegamenti. Il primo, detto chiuso, identifica un collegamento a triangolo. Il secondo, detto aperto, è definito collegamento a stella ed ha la caratteristica di presentare un punto in comune tra i tre bipoli detto centro stella. La figura di lato (un click per ingrandirla) mostra una stella di resistenze all’interno di un triangolo di resistenze afferenti negli stessi punti. Della figura in questione gli interessati potranno trovare lo snippet in TeX-LaTeX al seguente indirizzo.

In questo contesto, come riportato nel titolo, si vuole dimostrare che è sempre possibile sostituire tre resistenze che si collegano a triangolo in tre specifici punti con altre tre resistenze in topologia a stelle con estremi facenti capo agli stessi punti del triangolo senza alterare il funzionamento della rete elettrica.

Altrimenti detto, ogni triangolo di resistenze lineari può essere sempre trasformata in una ed una sola stella di resistenze e viceversa.

Trasformazione Triangolo-Stella di resistenze

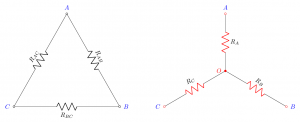
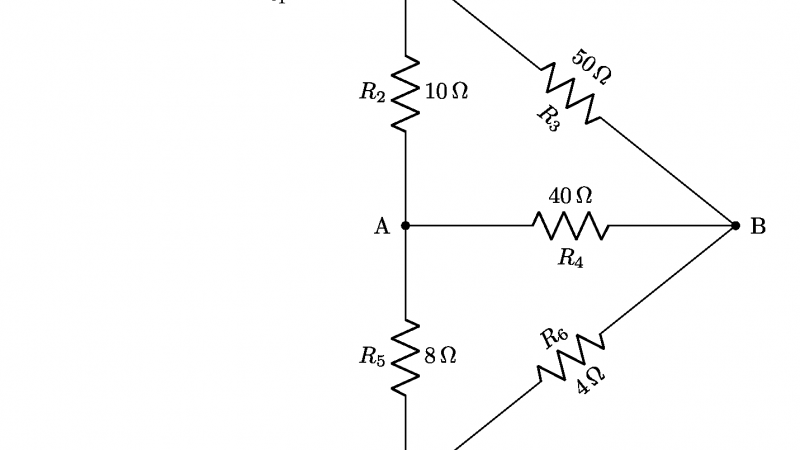
L’obiettivo è valutare analiticamente le formule che permettono il passaggio dal gruppo di resistenze a triangolo – riportate in colore nero nella figura a lato (un click sopra di essa per ingrandirla) – al gruppo di resistenze a stella riportate in colore rosso.

La resistenza vista dai punti C e B nel caso di collegamento a triangolo è pari alla serie delle due resistenze R_{AC} e R_{AB} posta in parallelo alla resistenza R_{BC}. In formula:

R_{BC_\Delta}=R_{BC}\|(R_{AC} + R_{AB})

Per gli stessi punti la resistenza vista nel collegamento a stella è pari alla serie di R_C e R_B (il punto A è aperto), pertanto:

R_{BC_Y}=R_C + R_B

Le due equazioni scritte possiamo riunirle in un sistema come:

\left \{  \begin{array}{ll} R_{BC_\Delta}=R_{BC}\|(R_{AC} + R_{AB})\\R_{BC_Y}=R_C + R_B \end{array} \right.

È possibile seguire la stessa dinamica per i punti A e C ottenendo:

\left \{  \begin{array}{ll} R_{AC_\Delta}=R_{AC}\|(R_{AB} + R_{BC})\\R_{AC_Y}=R_A + R_C \end{array} \right.

Infine per i punti A e B:

\left \{  \begin{array}{ll} R_{AB_\Delta}=R_{AB}\|(R_{BC} + R_{AC})\\R_{AB_Y}=R_A + R_B \end{array} \right.

Nella connessione a triangolo i paralleli delle resistenze possono essere riscritti come:

\left \{ \begin{array}{lll} R_{BC_\Delta}=\frac{R_{BC}\times(R_{AC}+R_{AB})}{R_{BC}+R_{AC}+R_{AB}} \\[1.1ex] \\ R_{AC_\Delta}=\frac{R_{AC}\times(R_{AB}+R_{BC})}{R_{BC}+R_{AC}+R_{AB}} \\[1.1ex] \\ R_{AB_\Delta}=\frac{R_{AB}\times(R_{BC}+R_{AC})}{R_{BC}+R_{AC}+R_{AB}} \end{array} \right.

Affinché la risultante topologia a stella risulti equivalente, ai fini della rete, a ciò che viene visto con la topologia di partenza a triangolo, occorre che il valore di resistenza vista dai punti C e B nella connessione a stella sia uguale a quella a triangolo; in buona sostanza R_{BC_\Delta}=R_{BC_Y}.

Medesime considerazioni per la coppia di punti A e C e per l’ultima coppia A e B. Questo porta al seguente sistema di 3 equazioni nelle 3 incognite resistenze a stella o a triangolo in funzione della topologia nota.

\left \{  \begin{array}{lll} \frac{R_{BC}\times(R_{AC} + R_{AB})}{R}=R_C+R_B \kern{1cm}(1) \\[1.1ex] \\ \frac{R_{AC}\times(R_{AB} + R_{BC})}{R}=R_A+R_C \kern{1cm}(2) \\[1.1ex]\\ \frac{R_{AB}\times(R_{BC} + R_{AC})}{R}=R_A+R_B \kern{1cm}(3) \end{array} \right.

laddove R=R_{BC}+R_{AC}+R_{AB}.

Si sta ipotizzando di partire con una topologia a triangolo pertanto le resistenze note sono R_{BC}, R_{AC}, R_{AB} mentre le incognite risultano R_A, R_B, R_C.

Dal sistema precedente sottraendo “a rotazione” 2 equazioni e aggiungendo la rimanente si otterranno le formule di trasformazione triangolo-stella. Ad esempio (3)-(1)+(2) da la prima equazione, infatti facendo la differenza membro a membro (3)-(1) risulta (barrando i termini che poi si semplificano):

\frac {\cancel{R_{AB}\times R_{BC}}+R_{AB}\times R_{AC}-R_{BC}\times R_{AC}-\cancel{R_{BC}\times R_{AB}}}{R}=\\[1.5em]=R_A+\cancel{R_B}-R_C-\cancel{R_B}

A questo punto si somma membro a membro la (2) ottenendo, al solito barrando i termini semplificabili:

\frac {R_{AB}\times R_{AC}-\cancel{R_{BC}\times R_{AC}}+R_{AC}\times R_{AB}+\cancel{R_{AC}\times R_{BC}}}{R}=\\[1.5em]=R_A-\cancel{R_C}+R_A+\cancel{R_C}

che porta a:

2\times \frac{R_{AB}\times R_{AC}}{R}=2\times R_A

ovvero, esplicitando a denominatore il valore di R e semplificando il 2 a destra e sinistra, la prima formula di trasformazione triangolo-stella:

R_A=\frac{R_{AB}\times R_{AC}}{R_{BC}+R_{AC}+R_{AB}}

Per calcolare il valore di R_B è sufficiente ripetere lo stesso iter per (1)-(2)+(3). Infine per la R_C si ha (2)-(3)+(1).

Prima di riportare le 3 formule complete si fa notare come esiste un modo mnemonico per ricordare le formule: ad esempio prendendo il nodo A della topologia a triangolo, la corrispondente R_A nella topologia a stella è pari al prodotto delle resistenze afferenti il nodo A nel triangolo, ovvero R_{AC}\times R_{AB} , diviso la somma delle resistenze del triangolo R_{BC}+R_{AC}+R_{AB}. Esattamente la formula ottenuta sopra.

Ad esempio R_B vede al numeratore il prodotto R_{AB}\times R_{BC} diviso R_{BC}+R_{AC}+R_{AB}. Stessa considerazione per la R_C.

In definitiva le formule per la trasformazione triangolo-stella di resistenze sono:

\left \{  \begin{array}{lll} R_A=\frac{R_{AB}\times R_{AC}}{R_{BC}+R_{AC}+R_{AB}}\\[1.5ex] R_B=\frac{R_{AB}\times R_{BC}}{R_{BC}+R_{AC}+R_{AB}}\\[1.5ex] R_C=\frac{R_{BC}\times R_{AC}}{R_{BC}+R_{AC}+R_{AB}}\end{array} \right.

Trasformazione Stella-Triangolo di resistenze

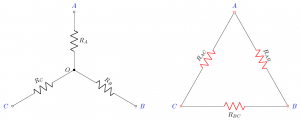
Per questo tipo di trasformazione si ipotizza di conoscere le resistenze nella connessione a stella, ovvero R_A, R_B, R_C (figura a lato) con l’obiettivo di ricavarsi le corrispondenti resistenze a triangolo R_{BC}, R_{AC}, R_{AB} (in rosso). Come procedere?

Conoscendo – risultato precedente – le formule per la trasformazione Triangolo-Stella, è possibile determinare i tre prodotti R_A\times R_B, R_B\times R_C, R_A\times R_C riportati nel seguito:

\left \{  \begin{array}{lll} R_A\times R_B=\frac{R_{AB}^2 \times R_{AC}\times R_{BC}}{(R_{BC}+R_{AC}+R_{AB})^2}\\[1.5ex] R_B\times R_C=\frac{R_{BC}^2\times R_{AB}\times R_{AC}}{(R_{BC}+R_{AC}+R_{AB})^2}\\[1.5ex] R_A\times R_C=\frac{R_{AC}^2\times R_{AB}\times R_{BC}}{(R_{BC}+R_{AC}+R_{AB})^2}\end{array} \right.

Sommando membro a membro le tre equazioni e semplificando i termini semplificabili, risulta:

R_A\times R_B+R_B\times R_C+R_A\times R_C=\\[1.2em]=\frac {R_{AB}^2 \times R_{AC}\times R_{BC}+R_{BC}^2\times R_{AB}\times R_{AC}+R_{AC}^2\times R_{AB}\times R_{BC}}{(R_{BC}+R_{AC}+R_{AB})^2}=\\[1.2em]=\frac{R_{AB}(R_{AB}\times R_{AC}\times R_{BC})+R_{BC}(R_{BC}\times R_{AB}\times R_{AC})+R_{AC}(R_{AC}\times R_{AB}\times R_{BC})}{(R_{BC}+R_{AC}+R_{AB})^2}=\\[1.2em]=\frac{\cancel{(R_{BC}+R_{AC}+R_{AB})}}{(R_{BC}+R_{AC}+R_{AB})\cancel{^2}}\times (R_{AC}\times R_{AB}\times R_{BC})

in definitiva:

R_A\times R_B+R_B\times R_C+R_A\times R_C=\frac{R_{AC}\times R_{AB}\times R_{BC}}{R_{BC}+R_{AC}+R_{AB}}\kern{1cm}(4)

nella quale “separando”, ad esempio, R_{AB} al secondo membro risulta:

R_A\times R_B+R_B\times R_C+R_A\times R_C=R_{AB}\times \frac{R_{AC}\times R_{BC}}{R_{BC}+R_{AC}+R_{AB}}

Ma la parte frazionaria è proprio la  R_C (vedere formule di trasformazione triangolo-stella) pertanto sostituendola da luogo a:

R_A\times R_B+R_B\times R_C+R_A\times R_C=R_{AB}\times R_C

e dalla quale è possibile ricavare la R_{AB}, resistenza triangolo punti A e B, in funzione delle resistenze note della topologia a stella:

R_{AB}=R_A+R_B+\frac{R_A\times R_B}{R_C}

Iterando il procedimento partendo sempre dalla (4) e “separando” dapprima R_{AC} e R_{BC} la parte frazionaria rimanente coincide con una delle formule per la trasformazione triangolo-stella viste in precedenza.

In definitiva le formule per la trasformazione stella-triangolo che conclude la dimostrazione:

\left \{  \begin{array}{lll} R_{AB}=R_A+R_B+\frac{R_A\times R_B}{R_C}\\[1.2ex] R_{BC}=R_B+R_C+\frac{R_B\times R_C}{R_A}\\[1.2ex]R_{AC}=R_A+R_C+\frac{R_A\times R_C}{R_B}\end{array} \right.

Un esempio

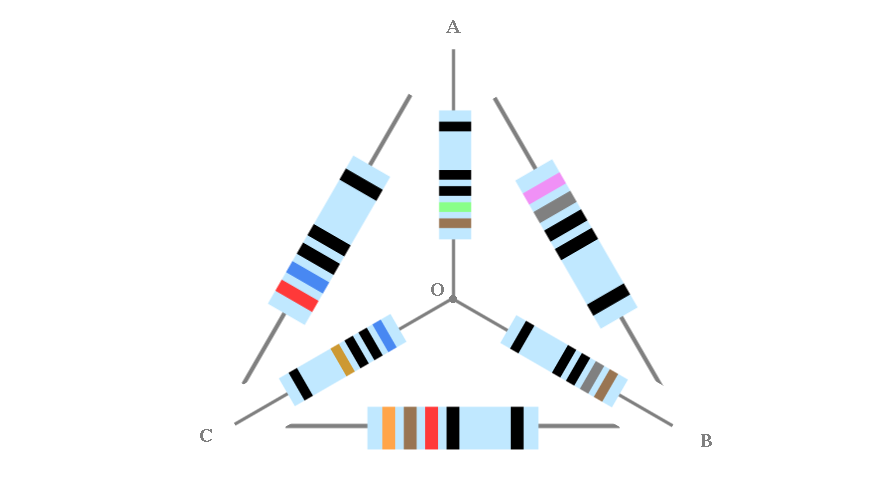
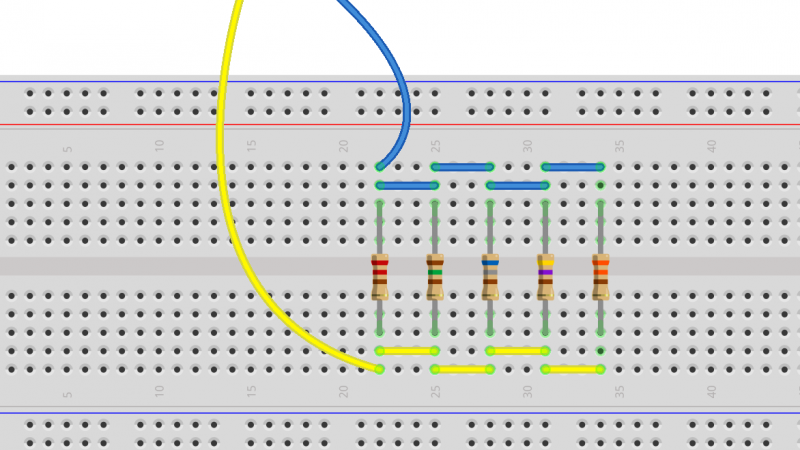
L’immagine di apertura mostra 3 resistenze collegate a triangolo e 3 collegate a stella. Il codice dei colori a 5 bande codifica i relativi valori; si ipotizzano le resistenze ideali con una tolleranza dello 0% (quinta banda color nero).

In questo scenario è facile verificare come R_{AC}=270\Omega, R_{AB}=780\Omega, R_{BC}=312\Omega. Da questi valori, utilizzando le note formule di trasformazione triangolo-stella, è possibile risalire ai valori delel resistenze in connessione a stella nelle quali R_A=150\Omega, R_B=180\Omega, R_C=60\Omega.

In maniera simile, dai valori riportati nella topologia a stella è possibile ottenere i corrispondenti a triangolo utilizzando le formule di trasformazione stella-triangolo sopra dimostrate.