Esempio 2cc: Trasformazione Triangolo-Stella

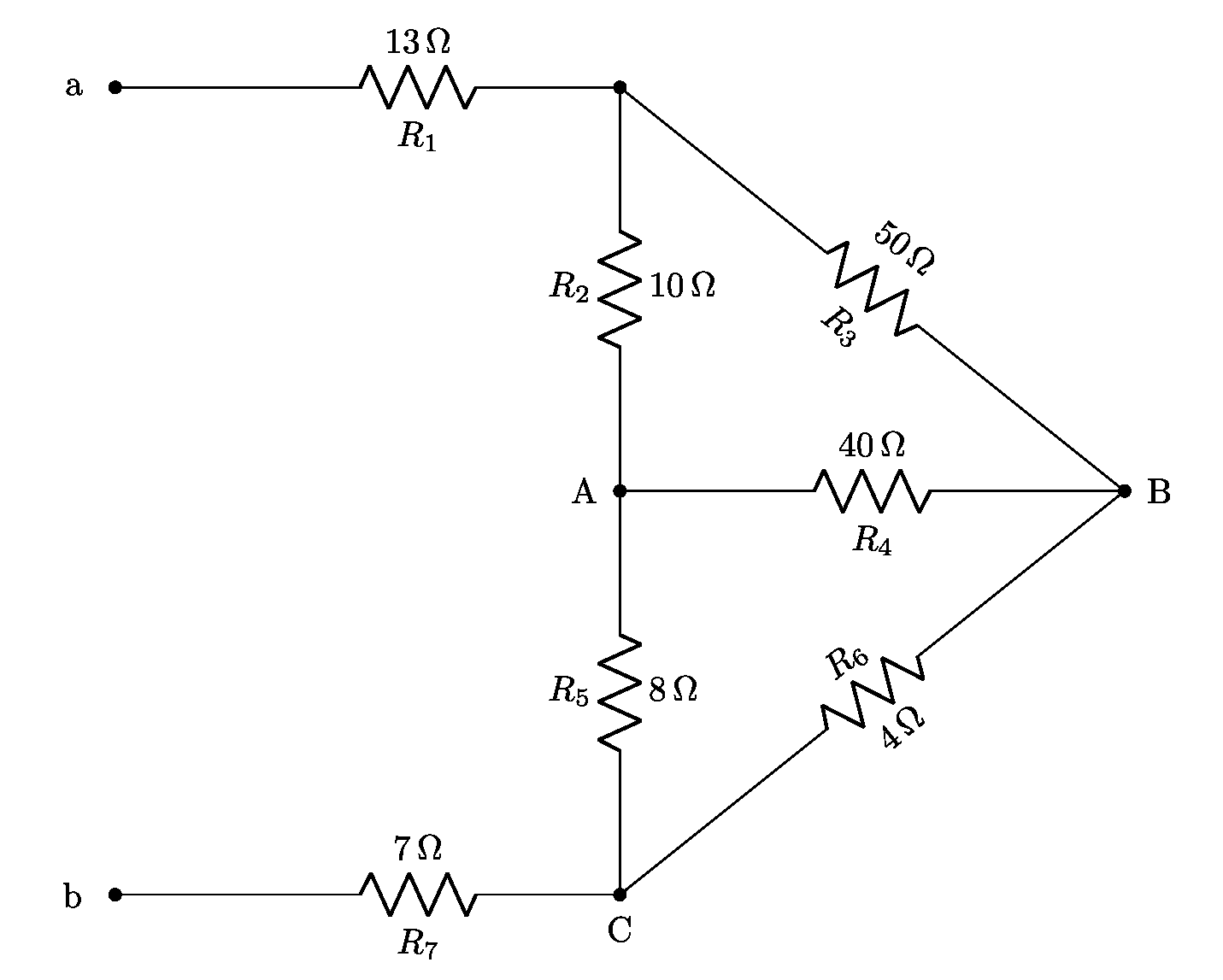
La topologia di partenza è la rete riportata nell’immagine di apertura: calcolare la resistenza equivalente R_{ab} vista dai punti a e b.

Trattasi, in verità, di un esempio molto discusso in rete. Infatti sono presenti anche diversi video su YouTube a tal proposito quindi è una topologia circuitale molto comune. Una base di partenza per comprendere la trasformazione triangolo-stella o stella-triangolo.

In questo contesto viene richiesta una trasformazione dal triangolo di resistenze collegate nei punti A, B e C nell’equivalente topologia a stella.

NOTA: da osservare come la semplificazione della rete sia possibile anche attraverso altre trasformazioni, ad esempio da stella a triangolo prendendo come riferimento le resistenze connesse a stella R_3, R_4, R_6 o anche il gruppo R_2, R_5, R_4 o, infine, considerare il triangolo composto da R_2, R_3, R_4 da trasformarsi in stella.

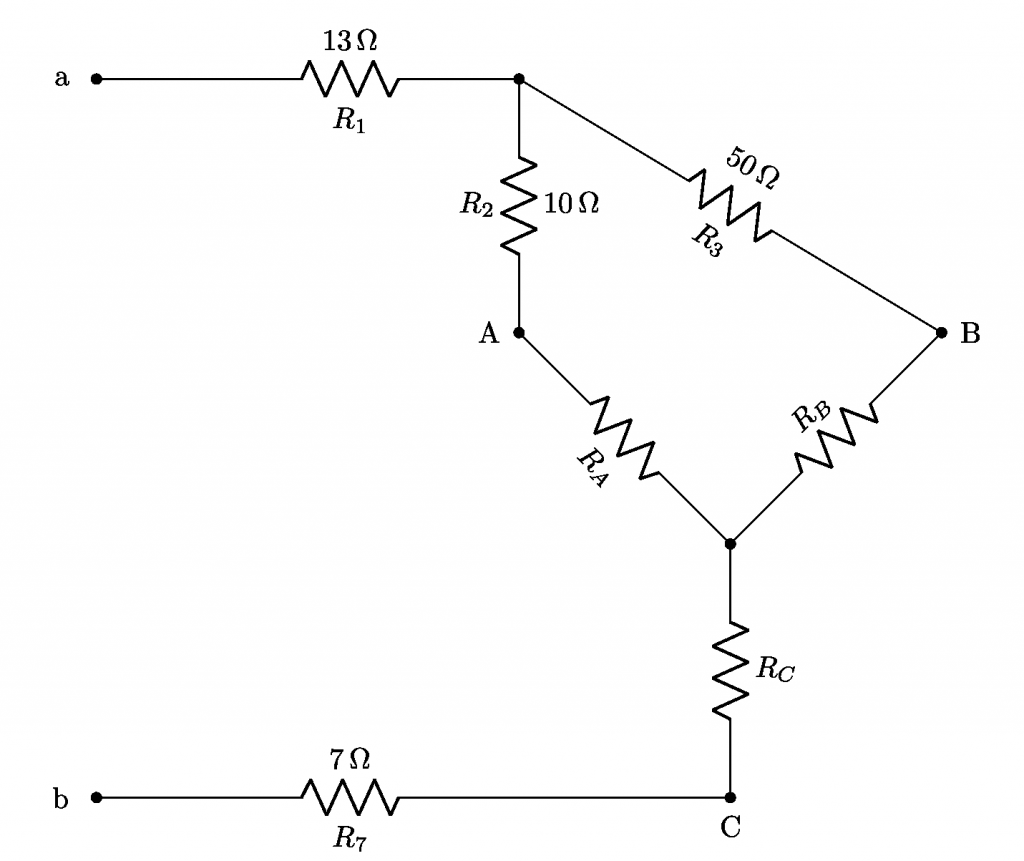
La nuova topologia circuitale – dopo aver trasformato il triangolo di resistenze ABC nella topologia a stella – è visibile nell’immagine in basso. Si fa presente che l’insieme delle due immagini, quella di apertura e quella in basso, è possibile disegnarle in \TeX/\LaTeX e il cui snippet è consultabile al seguente indirizzo.

La risoluzione a questo punto à piuttosto immediata. Facendo uso delle formule di trasformazione da triangolo a stella si ottiene:

\left \{  \begin{array}{lll} R_A=\frac{R_{AB}\times R_{AC}}{R_{BC}+R_{AC}+R_{AB}}=\frac{R_4\times R_5}{R_4+R_5+R_6}=\frac{40\times 8}{40+8+4}\cong 6,15\Omega\\[1.5ex] R_B=\frac{R_{AB}\times R_{BC}}{R_{BC}+R_{AC}+R_{AB}}=\frac{R_4\times R_6}{R_4+R_5+R_6}=\frac{40\times 4}{40+8+4}\cong 3,08\Omega\\[1.5ex] R_C=\frac{R_{BC}\times R_{AC}}{R_{BC}+R_{AC}+R_{AB}}=\frac{R_6\times R_5}{R_4+R_5+R_6}=\frac{4\times 8}{40+8+4}\cong 0,62\Omega\end{array} \right.

È facile ora verificare dalla figura in alto come vi siano due rami in parallelo costituiti dalla serie della resistenza R_A con la R_2 nel ramo di sinistra e dalla serie della resistenza R_B con R_3 nel ramo di destra. Questo permette di trovare la resistenza equivalente, ricordando la formula per il parallelo di resistenze, come:

R=(R_2+R_A) \parallel (R_3+R_B)=\\[1.5ex]=\frac{(R_2+R_A) \times (R_3+R_B)}{(R_2+R_A)+(R_3+R_B)}=\frac{(10+6,15) \times (50+3,08)}{(10+6,15)+(50+3,08)}\cong 12,38\Omega

Nel nuovo circuito equivalente, che non verrà riportato vista la sua semplicità e ovvietà, ora vi sono 4 resistenze in serie. Partendo dal punto a in alto e procedendo verso il punto b si ha R_1, la R calcolata poco sopra, la R_C e infine la R_7 tutte di valore noto pertanto la resistenza equivalente R_{ab}, che conclude l’esempio, sarà pari a:

R_{ab}=R_1+R+R_C+R_7=13+12,38+0,62+7=33\Omega